重ね合わせの「不確実性」：ノイズを体験する量子測定の実践

前回の記事では、量子プログラミングの「操作命令」（量子ゲート）と「文法」（量子回路図）の基礎を学習しました。
Xゲートで状態を反転させ、Hゲートで重ね合わせの状態を作る、基本的な操作は完璧です。

しかし、まだ大きな疑問が残っています。
なぜ、私たちが作る回路は、測定するたびに |0⟩ と |1⟩ の結果が「約50%ずつ」というランダムな確率で出てくるのでしょうか？
この「不確実性」こそが、量子コンピュータの核心です。

今回のゴールは、このランダムさの理論的な仕組み（量子測定のルール）を深く理解することです。
さらに、実機で必ず発生する「ノイズ」の影響を、ローカルシミュレーターを使って意図的に体験します。

では早速、この量子の海に隠された「確率」の法則を探りに行きましょう。

第1章：不確実性の核心、量子測定の仕組み

量子プログラミングの学習において、最もユニークでつまずきやすいのが「測定」です。
この章では、そのランダムさの根源である「測定のルール」を直感的に理解しましょう。

①量子状態は「確率」そのものである

古典コンピュータのビットは 0 か 1 のどちらかに確定していますが、量子ビットは「重ね合わせ」の状態にあります。

この重ね合わせの状態は、単なる 0 と 1 の中間ではなく、「0 になる確率の波」と「1 になる確率の波」が同時に存在している状態です。

量子状態を表現する |0⟩ や |1⟩ の記号（ケット）は、実際には確率の大きさと位相（波のズレ）という二つの情報を持っています。

②測定の瞬間：「確率の崩壊」

量子ビットを測定する瞬間、以下の2つのルールが働きます。

古典ビットの役割：測定結果の保管庫

前回記事のプログラムで作成した量子回路図で、測定ゲート（メーターのアイコン）の下に描かれている二重線を古典ビット（C）と呼びました。
※ 下図の緑枠で囲んだ個所です。

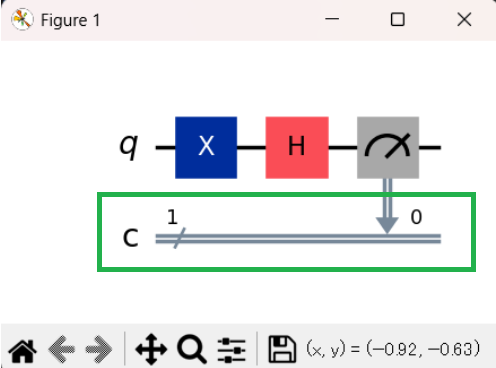
量子計算は非常に高速ですが、その測定結果は古典ビットのラインに送られ、通常のコンピュータが理解できる 0 または 1 として記録されます。

古典ビットは、量子ビットのような重ね合わせの状態は持てず、単に測定というイベントの結果を保管する役割を果たします。

第2章：実践：測定の仕組みをコードで確認

第2回で実行した、Xゲートと Hゲートを使った重ね合わせの回路を再実行します。
今回は、測定が行われる場所とその意味を特に意識しながらコードを見ていきましょう。

まだプログラムを作成していない方は、前回の記事を参照いただきコーディングしておいてください。

①量子回路の定義コード

プログラムの中で、以下のコードが量子回路を定義し、量子状態を |1⟩ に反転させ、その後Hゲートで 50/50 の重ね合わせ状態を作り出します。

最後の1行で、量子計算の終わりに「測定」という操作を実行しています。

# 1量子ビット、1古典ビットの回路を作成
circuit = QuantumCircuit(1, 1)

# ① Xゲートの適用：初期状態 |0⟩ を |1⟩ に反転させる
# 引数の「0」はインデックス
circuit.x(0)

# ② Hゲートの適用：重ね合わせ状態にする
# 引数の「0」はインデックス
circuit.h(0)

# ③ 測定：結果を取り出す
# 引数は2つともインデックス
circuit.measure(0, 0)

②プログラムの実行と結果の解釈

コード上で特に注目すべきは、以下の行です。

sampler = Sampler()

上記のサンプラー（シミュレーター）が、第1章で学んだ「確率の崩壊（ランダムな結果の確定）」を再現してくれます。

続くコードは以下のようになっています。
この部分のコード説明は「#」から始まるコメントとして記載しています。

# 作成した回路をシミュレーターで実行し、結果をジョブとして取得（1000回測定）
job = sampler.run(circuit, shots=1000)
# ジョブが完了するのを待ち、最終的な測定結果オブジェクトを取得
result = job.result()

# 結果オブジェクトから、最初の回路の測定確率分布（counts）を取り出す
counts = result.quasi_dists[0]

# ----------------------------------
# 実行結果のコンソール出力
# ----------------------------------

# 測定結果の分布（例: {0: 0.509, 1: 0.491}）をコンソールに出力
print("\n--- 測定結果 ---")
print(f"結果の分布（確率）： {counts}")

実行すると、以下のような（数値は人によって異なる）結果が得られます。
※ 今回はグラフの描画は省略します。

--- 測定結果 ---
結果の分布（確率）： {0: 0.509, 1: 0.491}

• 0 と 1 のキー：測定によって古典ビット（量子回路図のCライン）に記録された値です。
• 値 (0.5前後の数値)：第1章で学んだ「確率の大きさ」に従い、ランダムに 0 または 1 に確定した回数の割合です。

このプログラムでは、理論的に完璧なシミュレーター（Sampler）を使って、50/50の結果を再現しました。

しかし、現実の量子コンピュータ（実機）は常にエラーやノイズの影響下にあります。
実機をスムーズに使うためには、このノイズを避けて通ることはできません。

次章では、この「実機の現実」を体験するため、シミュレーターの種類を切り替え、意図的にノイズを回路に組み込んでみましょう。

第3章：実機への架け橋：シミュレーターでノイズを体験する

第1章で、理想的な環境では測定結果が「確率の崩壊」によって 50/50 に確定することを確認しました。
しかし、現実の量子コンピュータ（実機）は、非常に繊細なため、常にエラー（ノイズ）の影響を受けています。

このノイズこそが、実機とシミュレーターの決定的な違いです。
ここでは、実機の結果を正しく解釈する能力を養うため、ローカルシミュレーターに意図的にノイズを組み込みます。

①既存コードを書き換える方針

今回は、量子回路の定義（Xゲートと Hゲートの部分）はそのままにし、実行部分だけを書き換えます。

既存のコードの実行部分だけを書き換えることで、「量子回路の設計（X, Hの操作）は変わっていないのに、実行環境を変えただけで結果がどう変わるか」を明確に比較できます。
これは、ノイズの概念を理解する上で最も効率的で重要な学習方法です。

②冒頭のimport分の変更箇所

今回はSamplerを使わないため消去します。
代わりに、NoiseModelとdepolarizing_errorをインポートします。

from qiskit.circuit import QuantumCircuit
from qiskit_aer import AerSimulator
from qiskit_aer.noise import NoiseModel, depolarizing_error
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt

③量子回路の定義コードは変更なし

以下のコードには変更はありません。

# ----------------------------------
# 回路の定義 (X, Hゲート) は変更なし
# ----------------------------------
circuit = QuantumCircuit(1, 1)
circuit.x(0)
circuit.h(0)

circuit.measure(0, 0)

④変更後のコード全文

前項③の量子回路の定義以降のコードは、大幅に変更しますので、ここで変更後のコード全文を掲載します。

なお、今回はノイズの体験という今回の学習目的に焦点を絞るため、量子回路図は使いません。
よって、「回路図の描画（図の作成）」部分のコードは変更はありません。

from qiskit.circuit import QuantumCircuit
from qiskit_aer import AerSimulator
from qiskit_aer.noise import NoiseModel, depolarizing_error
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt

# 1量子ビット、1古典ビットの回路を作成
circuit = QuantumCircuit(1, 1)

# ① Xゲートの適用：初期状態 |0⟩ を |1⟩ に反転させる
# 引数の「0」はインデックス
circuit.x(0)

# ② Hゲートの適用：重ね合わせ状態にする
# 引数の「0」はインデックス
circuit.h(0)

# ③ 測定：結果を取り出す
# 引数は2つともインデックス
circuit.measure(0, 0)

# ----------------------------------
# ノイズモデルの定義と適用
# ----------------------------------

# ゲート実行時に0.5%の確率でエラーが発生するノイズモデルを作成
# depolarizing_error: 量子状態をランダムに破壊する一般的なノイズ
error_rate = 0.005 
# 1量子ビット操作(u1, u2, u3は単一ゲートの基本操作を指す)にノイズを設定
error = depolarizing_error(error_rate, 1)
custom_noise = NoiseModel()
custom_noise.add_all_qubit_quantum_error(error, ['u1', 'u2', 'u3', 'x', 'h']) 
# ↑ XゲートやHゲートの実行時にエラーを加える

# AerSimulatorに作成したノイズモデルを適用
simulator = AerSimulator(noise_model=custom_noise)

# ----------------------------------
# シミュレーターでの実行と可視化
# ----------------------------------

# ノイズを適用したシミュレーターで回路を実行 (shots=1000)
job = simulator.run(circuit, shots=1000)
result = job.result()

# 結果の取得とコンソール出力
counts = result.get_counts(circuit) # AerSimulatorはcountsで結果を取得
print("\n--- ノイズありの測定結果 ---")
print(f"結果の分布（カウント）： {counts}")
# 例: {0: 495, 1: 505} (理想は500:500だが、ノイズでランダムにブレる)

# ----------------------------------
# 可視化 (ヒストグラム)
# ----------------------------------
plot_histogram(counts, title='Result with 0.5% Depolarizing Noise')
plt.show()

# ----------------------------------
# 回路図の描画（図の作成）
# ----------------------------------

# 作成した量子回路を視覚化します
# 'mpl'を指定することで、matplotlibの描画形式で表示されます
circuit.draw("mpl")

# グラフ（回路図）を画面に表示します
# 回路図の画面を閉じると次のヒストグラムが表示されます
plt.show()

plt.close('all')

⑤実行結果の確認

このコードを実行すると、結果は理想的な 500 対 500 にはならず、理想の結果からわずかに「ブレ」たものになるはずです。

私の環境では以下のようになりました。
523 対 477 という結果で、Samplerを使用した時と比較するとかなり大きな差ができていることがわかります。

--- ノイズありの測定結果 ---
結果の分布（カウント）： {'1': 523, '0': 477}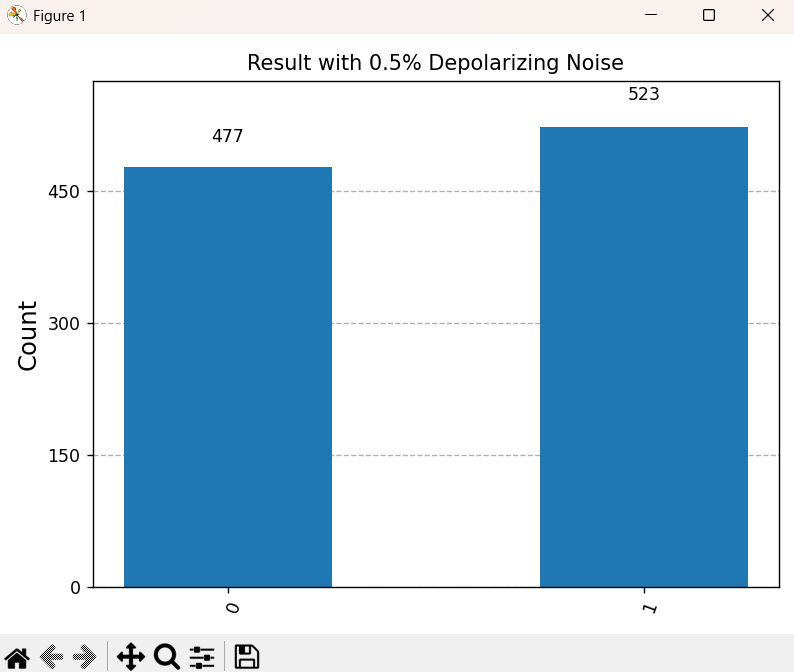

量子回路図

次章では、このブレた結果をどう解釈すべきか、そして、この体験がなぜ実機実行に不可欠なのかを詳しく解説します。

第4章：結果の解釈

第3章で実行したノイズありのコードをプログラミングして実際に試された方は、理想的な 50/50 の状態からわずかにブレた結果を示したはずです。
このブレの解釈こそが、私たちが実機の結果を正しく判断するための鍵となります。

①ノイズあり結果の解釈

理想的なシミュレーター（Sampler）を使っていた第2回では、結果は常に {0:∼0.5,1:∼0.5} と、完璧に近い値になりました。
しかし、ノイズを導入した AerSimulator の結果は、例えば {0:523,1:477} のように、わずかにどちらかに偏ることが確認できました。

この「ブレ」の正体が、実機で必ず発生するランダムなエラーです。
理想的な 50/50 の重ね合わせを H ゲートが作った後、その状態を測定するまでの間に、ノイズによって量子ビットがわずかに乱され、理想とは異なる結果（ノイズ）が古典ビットに記録されてしまったのです。

②なぜノイズの理解が必須なのか

実機を使うとき、結果は必ずこのノイズによってブレます。

1. ノイズへの耐性：
   • ノイズを体験することで、「ブレているけれど、これはノイズであってアルゴリズムが間違っているわけではない」と判断できるようになります。
2. 実機との比較：
   • ノイズの知識がなければ、実機の結果を見て「シミュレーターと結果が違う！」と戸惑ってしまいます。実機とローカルシミュレーターの結果を比較する際の誤差の範囲を事前に把握することができます。

まとめ

①今回の学習の総括

今回は、量子プログラミングの学習において極めて重要、且つユニークな部分である「不確実性」に真っ向から向き合いました。

• 測定のルールの理解：量子測定とは、量子ビットが持つ確率の波に基づき、ランダムに 0 か 1 のどちらかの状態に確定（崩壊）させる操作であることを理解しました。
• ノイズの体験：理想的な Sampler から、実機のノイズを再現する AerSimulator へと実行環境を切り替えました。意図的にノイズを組み込むことで、実機の結果が「ブレる」仕組みを体験的に把握しました。

②次回予告：アインシュタインも驚いた現象

次回の第4回記事では、いよいよ「真の量子コンピュータ」たる所以ゆえん、複数の量子ビットを連携させる操作に踏み込みます。

テーマは、かのアルベルト・アインシュタインが「不気味な遠隔作用」と呼んだことでも有名な現象、「量子もつれ（Entanglement）」です。

CNOTゲートという新しいゲートを使い、複数の量子ビットを切っても切れない関係にするコードを実装します。
この「もつれ」こそが、量子コンピュータが古典コンピュータよりも遥かに強力な計算力を発揮する根本的な力となります。