IBM量子コンピュータで実装するベル状態：HゲートとCNOTゲート

量子コンピュータ
2025.10.21

前回の記事で、私たちは qBraid のクラウド環境からIBMの実機に接続し、簡単なプログラム（Hello World）を動かすという、量子プログラミングの最初の大きな壁を突破しました。
単にシミュレーターを動かすのではなく、ノイズのある本物の量子コンピュータを操作する体験は、まさに感動的だったはずです。

しかし、前回はまだ「量子コンピュータらしい」ことはしていません。
今回は、いよいよ量子力学の最も強力な特徴である「重ね合わせ」と「量子もつれ」を実際に組み合わせて使います。

その鍵となるのが、量子の「最強コンビ」とも呼ばれるアダマールゲート（H）とCNOTゲートです。この2つのゲートをたった一度ずつ使うだけで、アインシュタインが「不気味な遠隔作用」と呼んだ「ベル状態」を生成できます。

本記事では、理論的な話は最小限に留め、早速PythonとQiskitを使ってベル状態を生成する量子回路をプログラミングし、IBM実機にジョブを送信します。
実機で得られた結果のデータを見ながら、「量子もつれ」がどのように現れるのかを具体的に確認していきましょう。

【シリーズ】量子コンピュータの世界メニューはこちら

目次

第1章：ベル状態とは ～量子の最強の相関

量子もつれの中でも最も単純かつ強力な形がベル状態です。
この状態を理解することが、量子プログラミングの核心に迫る第一歩となります。

①ベル状態の特徴（理論のミニマム）

ベル状態は、2つの量子ビット（ここではQubit 0とQubit 1）が最大限にもつれ合った状態です。

  • 重ね合わせ：量子ビット一つ一つは、 \(|0\rangle\) と \(|1\rangle\) の重ね合わせにあります。
  • 相関：2つの量子ビットの状態が強く結びついており、測定するまでどちらの状態になるかは分かりませんが、測定結果は必ず一致します。
    • Qubit 0が \(|0\rangle\) になったら、Qubit 1も必ず \(|0\rangle\) になる。
    • Qubit 0が \(|1\rangle\) になったら、Qubit 1も必ず \(|1\rangle\) になる。

この「瞬時に決まる」という相関が、アインシュタインが言うところの「不気味な遠隔作用」（非局所性）の根源です。

②ベル状態生成に必要な「最強コンビ」

ベル状態を生成するためには、2つのゲートを順番に適用するだけで十分です。

  1. アダマールゲート（H）：最初の量子ビット（Qubit 0）を「重ね合わせ」状態にし、計算の並列性を生み出します。
  2. CNOTゲート：「重ね合わせ」状態にあるQubit 0（制御）を用いて、Qubit 1（ターゲット）を操作することで、2つの量子ビットをもつれさせます。

この2つの操作が、ベル状態生成のすべてと考えて問題ありません。

第2章：qBraidからIBM実機への接続準備とモジュール化

ベル状態の量子回路を構築する前に、前回確立したqBraid環境からIBM Quantum Platformへの認証プロセスを再確認し、今後の連載で繰り返し使える（使いまわしできる）ように準備しましょう。

【重要】事前準備：qBraidへのアクセスとログイン

本章のコードを実行するためには、事前準備が必要です。
手順が不明な場合は、該当する以下の記事を参照いただき、設定作業を完了させてください。
※ プログラムは今回あらためて作成しますので、コーディングは不要です。

  1. IBM Quantum Platform へのアカウント登録とAPI Key取得（第2章まででOK）
  2. qBraid へのアカウント登録とAPI Key取得、各種設定

上記「事前準備」を完了させたばかりの方であれば、次の状態になっていると思います。

  • qBraidへのログイン後に「Launch Lab」の「Default Workspace」が開かれている状態
  • IBMのAPIトークンをqBraidに保存済

以前にそこまで進められた方は、Default Workspaceを起動しておいてください。

① 認証用モジュールファイル ibm_auth.py の作成と動作確認

今後のプログラムで認証コードを再利用するため、認証処理を ibm_auth.py というファイルにモジュールとして切り出します。

ステップ1：必要なライブラリのインストール

まず、ibm_auth.py で使用している qiskit_ibm_runtime を含む必要なライブラリをインストールします。

qBraid Labで新規のノートブックを作成してください。
名前は「bell_state_experiment.ipynb」とし、このノートブックを今回のメインとして使用していきます。

qBraidでの新規ノートブック作成手順

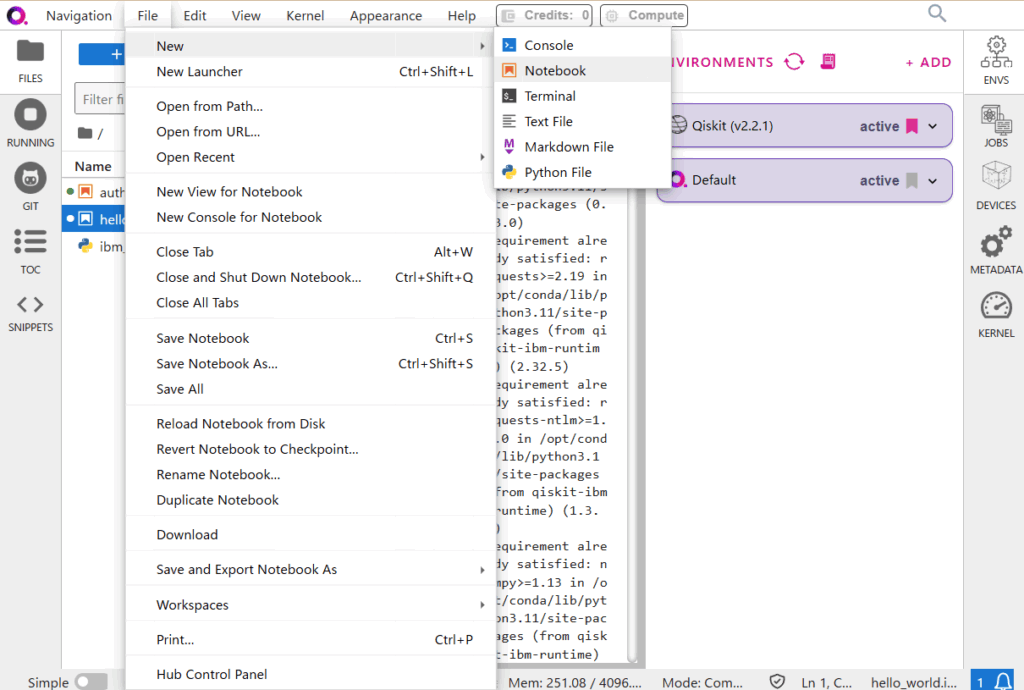
次に、ノートブックの最初のセル（セル1）に以下のコマンドを入力し、実行してください。

bell_state_experiment.ipynb (セル1)
!pip install qiskit-ibm-runtime pylatexenc --upgrade

ステップ2：モジュール用の新規ファイルを作成

以下の手順で、qBraid Labのファイルエクスプローラー（通常は左側）で新しいPythonファイルを作成し、名前を ibm_auth.py として保存してください。

qBraidでの新規Pythonファイル作成手順
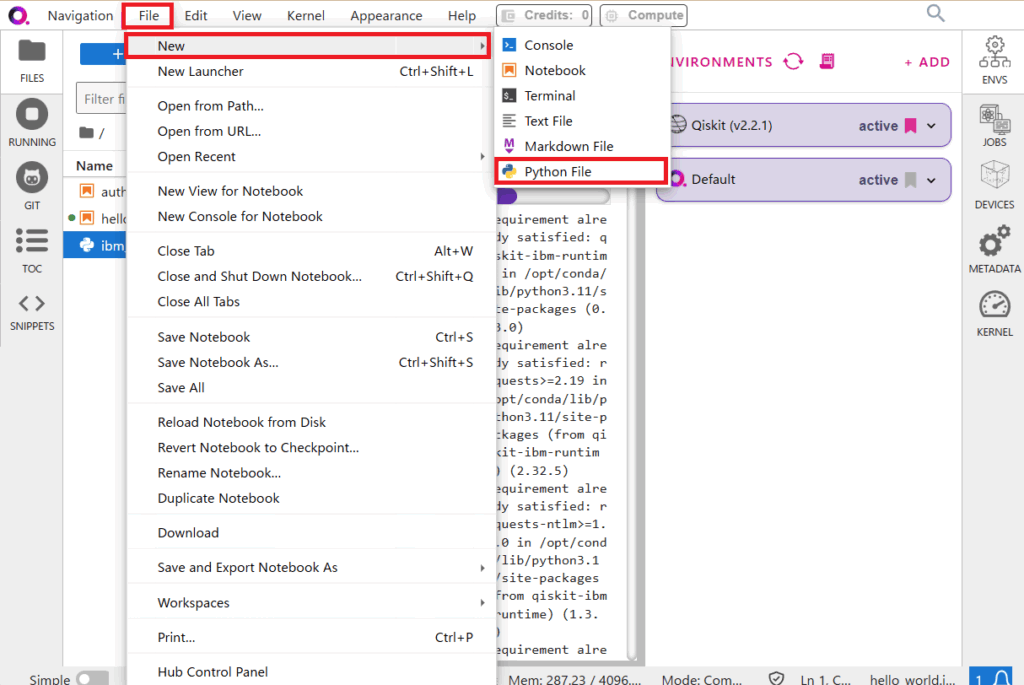
  1. ファイルを作成: 新規ファイルを作成し、ibm_auth.py と名前をつけます。
  2. APIキーの書き換え: 以下のコードを作成した ibm_auth.py に入力し、YOUR_API_KEY_HERE の部分を、ご自身の実際のIBM APIキー（文字列）に置き換えてください。
ibm_auth.py
from qiskit_ibm_runtime import QiskitRuntimeService

class IBM_CREDENTIALS:
    # ⚠️ 注意: YOUR_API_KEY_HEREをご自身のAPIキーに置き換えてください。
    API_KEY = "YOUR_API_KEY_HERE" 

def authenticate_and_get_service():
    """
    APIキーを使用して認証を行い、QiskitRuntimeServiceオブジェクトを取得する。
    """
    api_key = IBM_CREDENTIALS.API_KEY

    if not api_key or api_key == "YOUR_API_KEY_HERE":
        raise ValueError("APIキーが設定されていません。ibm_auth.py内のAPI_KEYを置き換えてください。")

    try:
        # Runtime Serviceを取得（ジョブ実行・実機選定用）
        service = QiskitRuntimeService(token=api_key)
        print("✅ IBM Quantum サービスへの認証が完了しました。")
        
        return service
    except Exception as e:
        print(f"❌ 接続エラーが発生しました: {e}")
        return None

ステップ3：認証テストの実行

ibm_auth.py ファイルを保存したら、作成済ノートブック「bell_state_experiment.ipynb」の二番目のセル（セル2）でモジュールをインポートして関数を実行し、認証が成功するかどうかを確認します。

この実行により、Serviceオブジェクトの取得も完了します。

bell_state_experiment.ipynb (セル2)
# 作成した認証モジュールのインポート
from ibm_auth import authenticate_and_get_service

# 認証オブジェクトを取得
service = authenticate_and_get_service()

# 接続成功の最終確認
if service:
    print("\n💡 認証に必要なServiceオブジェクトが取得できました！次のステップに進めます。")
else:
    print("\n❌ 接続に失敗しました。APIキーまたは設定を確認してください。")
実行結果

以下のとおり、設定した成功メッセージが表示されていればOKです。

② 利用可能なバックエンド（実機）の選定と確認

認証に成功した service オブジェクトを使って、ジョブを投げる最適な実機 (backend) を選定します。このコードは、実験ごとに毎回実行すべき内容です。

以下のコードを、メインノートブック「bell_state_experiment.ipynb」のセル3に記述し、実行して実機を選定します。

bell_state_experiment.ipynb (セル3)
# ----------------------------------------------------
# 後に別のセルで使用するためグローバルスコープで初期化
# ----------------------------------------------------
least_busy_backend = None

if service:
    # least_busy()を使って、最も空いている実機を直接選定（Qubit数2以上）
    least_busy_backend = service.least_busy(
        filters=lambda x: x.configuration().n_qubits >= 2 and not x.configuration().simulator
    )
    
    if least_busy_backend:
        print(f"[選定された実機] {least_busy_backend.name}")
        print(f"- Qubit数: {least_busy_backend.configuration().n_qubits}")
        print(f"- ジョブ待機数: {least_busy_backend.status().pending_jobs}")
        
        # 次のステップのためにbackendオブジェクトを保存
        backend = least_busy_backend
    else:
        print("利用可能な2Qubit以上の実機が見つかりませんでした。")
else:
    print("認証が完了していないため、実機選定をスキップします。")
実行結果

以下のようなメッセージが表示されれば成功です。
（※ [選定された実機]、Qubit数、ジョブ待機数の値はタイミング、ユーザーごとに変わります）

[選定された実機] ibm_brisbane
- Qubit数: 127
- ジョブ待機数: 3716

モジュール変更時の注意点：

プログラムを作成していると、タイプミスなどで内容を修正しなければならなくなる場合もあります。
特に外部ファイル（ibm_auth.py）を編集された際には、ノートブックでその変更を反映させるために、カーネルの再起動が必要になる場合があります。

もし ImportError などが出て解消されない場合は、「Restart Kernel」（カーネルの再起動）をお試しください。

なお、「Restart Kernel」は以下の手順でも可能です。

  1. qBraid Labのメニューバーから「Kernel（カーネル）」を選択する。
  2. メニュー内の「Restart Kernel」を実行する。
  3. ノートブックの最初のセル（セル1）から順番に再実行する。

第3章：HゲートとCNOTゲートを使用したベル状態回路の設計

第2章で、IBM実機への接続と、ジョブを送信する最適なバックエンド（量子コンピュータ）の選定が完了しました。
この第3章では、いよいよ今回のテーマであるベル状態（\(\vert\Phi^+\rangle\)）を生成するための量子回路を設計します。

ベル状態は、量子コンピュータの動作原理を理解する上で最も重要な概念である重ね合わせと量子もつれの二つが組み合わさって生まれる、基本的な量子現象です。

本章では、以下の手順で回路の設計を行います。

  1. ベル状態（\(\vert\Phi^+\rangle\)）の定義：ベル状態がどのような状態であるかを確認します。
  2. 必要なゲートの解説：状態の生成に必要なH（アダマール）ゲートとCNOT（制御NOT）ゲートの役割を理解します。
  3. 回路の論理設計の確認：HゲートとCNOTゲートの組み合わせがベル状態を生成する様子を数式と図で示し、Qiskitで使用する回路の論理構造を確定します。

① ベル状態（\(\vert\Phi^+\rangle\)）の定義

ベル状態は、2つの量子ビット（\(q_0, q_1\)）が完全に量子もつれの状態にあることを示す基本的な量子状態です。
特に今回作成する\(\vert\Phi^+\rangle\)（ファイ・プラス）状態は、最も基本的なベル状態です。

ベル状態 (\(\vert\Phi^+\rangle\)) の数式表現

ベル状態 \(\vert\Phi^+\rangle\) は、数学的には以下の重ね合わせとして定義されます。

\(\vert\Phi^+\rangle = \frac{1}{\sqrt{2}} (\vert 00\rangle + \vert 11\rangle)\)

この数式が意味するのは、以下の2点です。

  1. 重ね合わせ（Superposition）：この状態は、\(\vert 00\rangle\) と \(\vert 11\rangle\) という2つの基底状態が50%ずつ混合した状態にあることを示しています。\(\frac{1}{\sqrt{2}}\) は、確率振幅しんぷくの二乗（\(1/2\)）が確率になるための正規化係数です。
  2. 量子もつれ（Entanglement）：最も重要な点です。測定結果が必ず \(\vert 00\rangle\) か \(\vert 11\rangle\) のどちらかになるという相関関係が成立します。2つの量子ビットの状態は分離不可能であり、これが量子もつれの本質です。

ベル状態の生成に必要な初期状態

今回の回路は、2つの量子ビットが \(\vert 00\rangle\) という状態からスタートします。

数学的には以下のとおり定義されます。

\(\vert\psi_{\text{initial}}\rangle = \vert 00\rangle\)

② 必要なゲートの解説

ベル状態 \(\vert\Phi^+\rangle\) を初期状態 \(\vert 00\rangle\) から生成するために必要なゲートは、H（アダマール）ゲートとCNOT（制御NOT）ゲートの2つです。

②-1. H（アダマール）ゲート：重ね合わせの生成

アダマールゲートは、量子ビットを重ね合わせ状態にするための最も基本的なゲートで、記号は「H」す。

初期状態 \(\vert 0\rangle\) の量子ビットに作用させると、状態は \(\frac{1}{\sqrt{2}}(\vert 0\rangle + \vert 1\rangle)\) となり、0と1が50%ずつの確率で存在する状態になります。

この操作をケット記法で表すと以下の通りです。

\(\mathbf{H \vert 0\rangle \rightarrow \frac{1}{\sqrt{2}} (\vert 0\rangle + \vert 1\rangle)}\)

回路図では、Hゲートは単一の量子ビットの線上に四角形で描かれます。

\(\vert 00\rangle\) の状態に対し、\(q_0\) に Hゲートを適用すると、状態は \(q_0\) が重ね合わせになり、\(\frac{1}{\sqrt{2}}(\vert 00\rangle + \vert 10\rangle)\) となります。これが量子もつれの最初のステップとなります。

②-2. CNOT（制御NOT）ゲート：量子もつれの生成

CNOT（Controlled-NOT）ゲートは、ベル状態 \(\vert\Phi^+\rangle\) を生成するための決定的な役割を果たします。
このゲートによって、2つの量子ビット間に相関、すなわち量子もつれ（Entanglement）が作り出されます。

CNOTゲートは、以下の要素で構成される2量子ビットゲートです。

  • 制御量子ビット (Control Qubit): ゲートの動作を決定する量子ビットです。
  • ターゲット量子ビット (Target Qubit): 制御ビットの状態に基づいて反転操作を受ける量子ビットです。

CNOTゲートは、古典的な「IF-THEN」ロジックと似ています。

制御ビットの状態ターゲットビットへの作用結果
\(\vert 0\rangle\)ターゲットビットは変化しないターゲットの状態 \(\vert x\rangle\) は \(\vert x\rangle\) のまま
\(\vert 1\rangle\)ターゲットビットは反転（NOT操作）するターゲットの状態 \(\vert x\rangle\) は \(\vert 1-x\rangle\) になる

前のセクション（②-1）で、回路の状態は \(q_0\) にHゲートが適用された後の、重ね合わせ状態である \(\frac{1}{\sqrt{2}}(\vert 00\rangle + \vert 10\rangle)\) でした。

この状態に対し、\(q_0\) を制御ビット、\(q_1\) をターゲットビットとして CNOTゲートを適用することで、最終的なベル状態 \(\vert\Phi^+\rangle\) が完成します。

この操作をケット記法で表すと以下の通りです。

\(\text{CNOT} \left( \frac{1}{\sqrt{2}}(\vert 00\rangle + \vert 10\rangle) \right)\)

\(\rightarrow \frac{1}{\sqrt{2}} (\vert 00\rangle + \vert 11\rangle) = \vert\Phi^+\rangle\)

  1. \(\vert 00\rangle\) の項: 制御ビット \(q_0\) は \(\vert 0\rangle\) なので、ターゲット \(q_1\) は変化せず、\(\vert 00\rangle\) のまま。
  2. \(\vert 10\rangle\) の項: 制御ビット \(q_0\) は \(\vert 1\rangle\) なので、ターゲット \(q_1\) は反転し、\(\vert 11\rangle\) に変化。

これにより、2つの量子ビットの状態は分離不可能な \(\vert 00\rangle\) と \(\vert 11\rangle\) のもつれた重ね合わせとなり、ベル状態 \(\vert\Phi^+\rangle\) の設計が完了します。

③ 回路の論理設計の確認

③-1. ベル状態回路の完成図

ベル状態 \(\vert\Phi^+\rangle\) を初期状態 \(\vert 00\rangle\) から生成するために必要な操作は、以下の2ステップに集約されます。

  1. \(q_0\) への Hゲートの適用: 最初の量子ビット (\(q_0\)) を重ね合わせ状態にする。
  2. \(q_0\) 制御、 \(q_1\) ターゲットの CNOTゲートの適用: 重ね合わせ状態を \(q_1\) に伝播し、量子もつれを生成する。

③-2. Qiskitによる回路オブジェクトの準備

③-1の論理設計した回路を次章（第4章）で実装するため、Qiskitで回路の設計図となる量子回路オブジェクトを準備します。

量子回路（QuantumCircuit）のオブジェクトは、数行のプログラムコードを記述しますが、回路の論理的な枠組みを定義するものであり、この段階ではまだゲートの操作は記述しません。

以下の手順で回路オブジェクトを準備します。

  1. 必要なライブラリのインポート: qiskit.circuit モジュールから QuantumCircuit をインポートします。
  2. 回路オブジェクトの初期化: 2つの量子ビット（num_qubits=2）と、2つの古典ビット（num_clbits=2）を持つ回路を作成します。

ノートブック「bell_state_experiment.ipynb」のセル4に次のプログラムを入力してください。

bell_state_experiment.ipynb (セル4)
from qiskit.circuit import QuantumCircuit

# 2量子ビット、2古典ビットの回路を準備
# 古典ビットは最終的な測定結果を格納するために必要
qc = QuantumCircuit(2, 2)

print("量子回路オブジェクトを準備しました。")
print(f"量子ビット数: {qc.num_qubits}")
print(f"古典ビット数: {qc.num_clbits}")
実行結果
量子回路オブジェクトを準備しました。
量子ビット数: 2
古典ビット数: 2

以上で、回路の設計図と、それを実装するための Qiskit の枠組みが整いました！

第4章：ベル状態回路の実装と実機での実行

前章（第3章）では、ベル状態 (\(\vert\Phi^+\rangle\)) を生成するために必要なHゲートとCNOTゲートの作用を学び、回路の論理設計を確定しました。

その設計に基づき、本章では Qiskit コードを記述して回路を実装し、第2章で選定したIBMの量子コンピュータ実機にジョブを送信・実行します。

具体的には、以下の手順で作業を進めます。

  1. 量子回路の実装と描画: 第3章で準備した回路オブジェクトにゲートを適用し、最終的な回路図を確認します。
  2. 測定操作の追加と実行: 回路に測定操作を追加し、QiskitのSamplerプリミティブを使用して実機でジョブを実行し、結果を取得します。

① 量子回路の実装と描画

第3章で設計した論理構造（Hゲート \(\rightarrow\) CNOTゲート）を、Qiskitコードで実装します。

①-1. HゲートとCNOTゲートの適用

ベル状態 \(\vert\Phi^+\rangle\) の生成に必要な操作は以下の通りです。

  1. \(q_0\) にHゲートを適用 (qc.h(0))
  2. \(q_0\) 制御、 \(q_1\) ターゲットのCNOTゲートを適用 (qc.cx(0, 1))

ノートブック「bell_state_experiment.ipynb」のセル5に次のプログラムを入力してください。

bell_state_experiment.ipynb (セル5)
# ----------------------------------------------------
# 第3章の設計に基づき、ゲートを適用する
# ----------------------------------------------------

# 1. 最初の量子ビット (q0) にHゲートを適用 (重ね合わせ状態の作成)
qc.h(0)

# 2. q0を制御、q1をターゲットとしてCNOTゲートを適用 (量子もつれの作成)
qc.cx(0, 1)

print("✅ HゲートとCNOTゲートを回路に適用しました。")
実行結果

①-2. 回路図の描画による確認

ゲート操作を適用した後、回路図（設計図）を描画し、意図した通りの構造になっているかを確認します。

この図は、左から右に時間が進むことを示しており、Hゲートの後にCNOTゲートが続く構造になっているはずです。

ノートブック「bell_state_experiment.ipynb」のセル6に次のプログラムを入力してください。

bell_state_experiment.ipynb (セル6)
# 回路図を描画
# style="mpl"で視覚的に見やすいMatplotlib形式を使用
qc.draw(output='mpl', style='bw')

# 注：qBraid Lab環境では、このセル単独で実行すると図が表示されます。
# ノートブックをPDF等にエクスポートする際にも利用できます。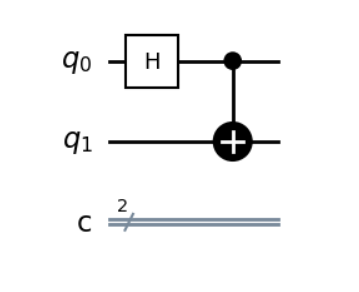
実行結果

このように視覚的な回路図が表示されれば成功です！

この回路図は、設計したベル状態回路（第3章を参照）が正しくコード化されたことを示しています。

② 測定操作の追加と実行

前のセクションで、ベル状態を生成するコアな量子ロジックの実装が完了しました。
しかし、量子コンピュータで結果を観測するには、量子ビットの状態を古典ビットに転送する測定操作を必ず回路に追加する必要があります。

このセクションでは、測定操作を追加し、Qiskitの最新の実行方法である SamplerV2プリミティブ を用いて、IBM量子コンピュータ実機での実行を行います。

②-1. 測定操作の追加

作成した量子回路オブジェクト qc に対し、各量子ビットの状態を対応する古典ビットに測定し、記録します。

ノートブック「bell_state_experiment.ipynb」のセル7に次のプログラムを入力してください。

bell_state_experiment.ipynb (セル7)
# 量子ビットの結果を古典ビットに測定・記録
qc.measure([0, 1], [0, 1])

# 測定後の回路を最終バージョンとして保存
qc_final = qc

print("✅ 量子回路に測定操作を追加し、実行準備完了です。")
実行結果
✅ 量子回路に測定操作を追加し、実行準備完了です。

これにより、回路は実機に送信できる最終的な状態になりました。

②-2. Samplerプリミティブを使用した実機での実行

測定操作が追加された qc_final を使用して、実機にジョブを送信します。
SamplerV2は、実機やシミュレーターでの実行結果（測定のカウント数）を効率的に取得するために推奨される手法です。

ノートブック「bell_state_experiment.ipynb」のセル8に次のプログラムを入力してください。

実行結果の提示と分析は次章（第5章）で行います。

bell_state_experiment.ipynb (セル8)
from qiskit_ibm_runtime import SamplerV2
from qiskit.visualization import plot_histogram
from qiskit import transpile

print(f"--- 🚀 実機 {least_busy_backend.name} へのジョブ送信を開始します ---")

# トランスパイルを実行
transpiled_circuit = transpile(
    qc_final, 
    backend=least_busy_backend, 
    optimization_level=3 # 最適化レベルは3を推奨
)

# 実行用回路をqc_finalに上書き保存
qc_final = transpiled_circuit

# SamplerV2プリミティブの初期化
sampler = SamplerV2(mode=least_busy_backend) 

# SamplerV2を使用してジョブを送信
job = sampler.run(
    pubs=[qc_final], # セル6で定義したqc_finalを使用
    shots=1024
)

print(f"✅ ジョブを送信しました。ジョブID: {job.job_id}")

# ジョブの完了を待機し、結果を取得
print("ジョブ完了を待機中です...")
result = job.result()

# 結果の取得とヒストグラム描画
counts = result[0].data["c"].get_counts() 

print(f"✅ 実機ジョブが成功しました！最終カウント:")
print(counts)

# 結果の棒グラフ表示（ヒストグラム）
plot_histogram(counts)

上記、セル8のプログラムは、前回記事の「量子版Hello World」の内容に加え、「ベル状態のジョブを実機に送信する」という処理が追加されています。
たったそれだけの違いですが、このプログラムの実行には、解決までに時間を要した重大な技術的課題が潜んでいました。

【課題】：実機が理解できない命令の存在

結論として、ベル状態回路のジョブを実機に送信するためには、トランスパイル（Transpile）処理が必須となりました。

今回は回路でHゲート（アダマールゲート）とCNOTゲート（CX）を使用しましたが、エラーメッセージはHゲートが実機のネイティブな命令セット（ISA）に含まれていないことを指摘しました。
しかし、それはHゲートが先にコーディングされていたため、エラー原因として表面化したに過ぎず、トランスパイルはHゲートのみならず、回路全体に対して必要と考えられます。

  1. Hゲート：実機はHゲートを直接実行できないため、トランスパイラがこれを複数の回転ゲートの組み合わせなどに分解・変換する必要があります。
  2. CNOTゲート（CX）：CXゲートはネイティブ命令に含まれることが多いですが、トランスパイルは実機の物理配線（カップリングマップ）に合わせて回路を最適化・再配置するために必要です。設計した\(q_0\)と\(q_1\)が実機で直接繋がっていなければ、トランスパイラがSWAPゲートの挿入などを行います。

【解決】：トランスパイルによる回路の最適化

この問題を解決するために、Qiskitのトランスパイラ機能を利用しました。

トランスパイルとは、人間が設計した理想的な量子回路を、選定された特定の実機（least_busy_backend）のネイティブゲートセットだけで構成される回路に自動的に変換し、最適化するプロセスです。

今回のケースでは、トランスパイルによってHゲートが、実機が実行可能な複数の回転ゲートやその他のネイティブな命令の組み合わせに自動で分解・変換されました。

このトランスパイル処理（qiskit.transpile(...)）を追加することで、ようやく実機が回路を認識し、ジョブの実行に成功しました。

第5章：実機実行結果の分析と量子ノイズの影響

前章で、設計したベル状態回路をIBM量子コンピュータ実機（ibm_torino）で実行し、結果を観測しました。
本章では、この結果を詳細に分析し、量子ノイズが結果に与える影響について考察します。

まずは実行結果を提示します。（画像の黄色枠内が実行結果です）

実行結果（セル8）

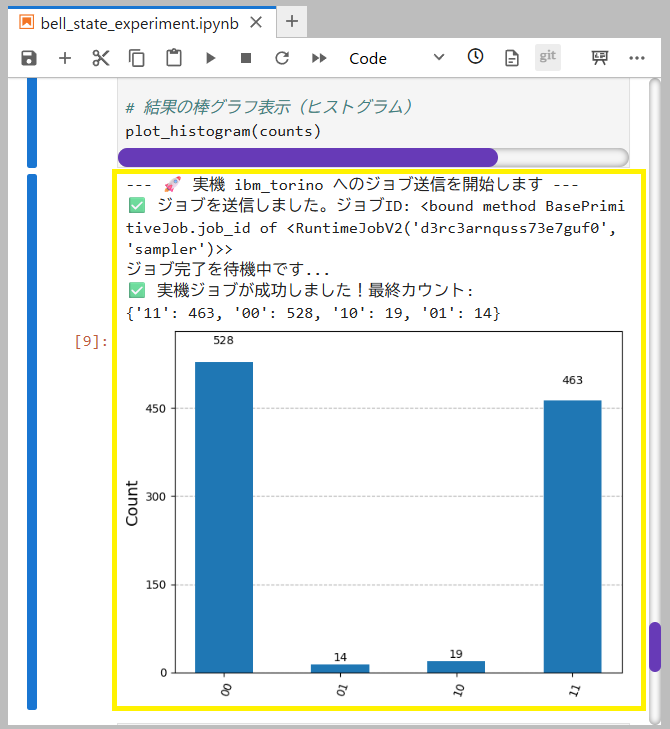
① 理論値と実測値の比較

ベル状態 \(|\Phi^+\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)\) の理想的な測定結果は、状態 \(\vert 00\rangle\) と \(\vert 11\rangle\) がそれぞれ50%ずつ観測されることです。

今回の実行結果（ショット数1024）を理論値と比較します。

状態観測回数
（理論上50%）		観測回数 (実測)偏差
\(\vert 00\rangle\)512回528回+16回
\(\vert 11\rangle\)512回463回-49回
エラー(\(\vert 01\rangle\)と\(\vert 10\rangle\))0回33回
(14 + 19)		+33回

実行結果の図として示されたヒストグラムの通り、結果のほとんどは期待された \(\vert 00\rangle\) と \(\vert 11\rangle\) に集中しており、量子もつれが正しく生成されたことが証明されました。

② 量子ノイズ（エラー）の分析

実機の結果では、理論的にはゼロであるはずの \(\vert 01\rangle\) (14回) と \(\vert 10\rangle\) (19回) の状態が合計で33回観測されました。
これは、量子ノイズ（量子ビットの誤り）によるものです。

ノイズの主な原因

これらのエラーは、主に以下の量子ノイズが原因で発生します。

  1. 量子ビットの誤り率（デコヒーレンス）：量子ゲートの実行中や、量子ビットが待機している間に、外部環境との相互作用によって状態が崩壊し、\(\vert 0\rangle\) が \(\vert 1\rangle\) に反転するなどのエラーが発生します。
  2. 測定エラー：最終的な測定時に、量子ビットの状態が正しく古典ビットに読み出されないことによるエラーです。特に \(\vert 00\rangle\) や \(\vert 11\rangle\) といった主要な結果の一部が測定エラーにより \(\vert 01\rangle\) や \(\vert 10\rangle\) として記録されたと考えられます。

この結果は、実機がノイズの影響下にある現実の量子コンピュータであることを示しており、このノイズの存在こそが、シミュレーターの結果と実機の結果を区別する最も重要な点です。

まとめ

本記事を通じて、読者の皆様は量子コンピューティングにおける最も重要かつ基本的な現象の一つである量子もつれ（ベル状態）を、理論から実機での実行まで一貫して経験しました。

今回得られた重要な教訓は次のとおりです。

  1. 理論の理解（ベル状態の構造）：量子もつれが「量子重ね合わせ」と「CNOTゲート」の組み合わせで生成されること、そしてその結果が\(\vert 00\rangle\)と\(\vert 11\rangle\)の重ね合わせとなることを、数式と回路図で確認しました。
  2. 実装の習得（Qiskitコード）：Qiskit SDKを使用し、回路の定義、実機の選定、測定操作の追加という一連のステップを学びました。
  3. 実機実行の現実（トランスパイルとノイズ）：
    • トランスパイルの必要性：汎用的なHゲートなどの命令を実機のネイティブゲートセットに変換するトランスパイル処理が、実機実行には不可欠であることを、エラーを通じて痛感し、習得しました。
    • 量子ノイズの影響：実機実行の結果、理論値にはなかった\(\vert 01\rangle\)や\(\vert 10\rangle\)のエラーが観測され、現実の量子コンピュータがノイズの影響下にあることをデータで確認しました。

次のステップとして、「量子もつれ」という基本をマスターした読者の皆さまは、この経験を土台として、量子アルゴリズム（例：グローバーのアルゴリズム、ショアのアルゴリズム）の実装と検証へとステップアップしていくことができます。

【シリーズ】量子コンピュータの世界メニューはこちら

スポンサーリンク

コメント

タイトルとURLをコピーしました