前回までで、「三角比」の基礎知識を完璧に習得しましたが、その内容は直角三角形の中でしか通用しません。
量子力学において、電子などの粒子は「波」として振る舞います。
波の動きを記述するためには、角度の制約を超え、さらにはマイナスの領域まで拡張しなければなりません。
この拡張された概念が、今回のテーマである「三角関数(Trigonometric Functions)」です。
三角関数とは、私たちが学んだ\(\sin, \cos, \tan\) の比率を、単位円(半径1の円)へと進化させたものです。
この円を使うことで、角度と \(\sin, \cos\) の値を座標として捉えられるようになり、無限の角度を自由に扱えるようになります。
本記事では、三角比を三角関数へ発展させる最重要ツール「単位円」を徹底的に解説し、最終的に、三角関数と複素数を結びつける量子力学の核心的ツール、「オイラーの公式」を理解するための土台を完成させます。
目次
- 1 第1章:三角比から三角関数への拡張
- 2 第2章:ラジアンと三角関数のグラフ
- 3 第3章:量子力学で必須の数学「オイラーの公式」と「複素数」
- 4 まとめ
第1章:三角比から三角関数への拡張
① 最重要ツール「単位円」の定義
前回までの三角比の定義では、\(\sin \theta = \frac{\text{対辺}}{\text{斜辺}}\) のように、比率でしか値を扱えませんでした。
ここで、三角比を三角関数へと進化させるための、最重要ツール「単位円」を導入します。
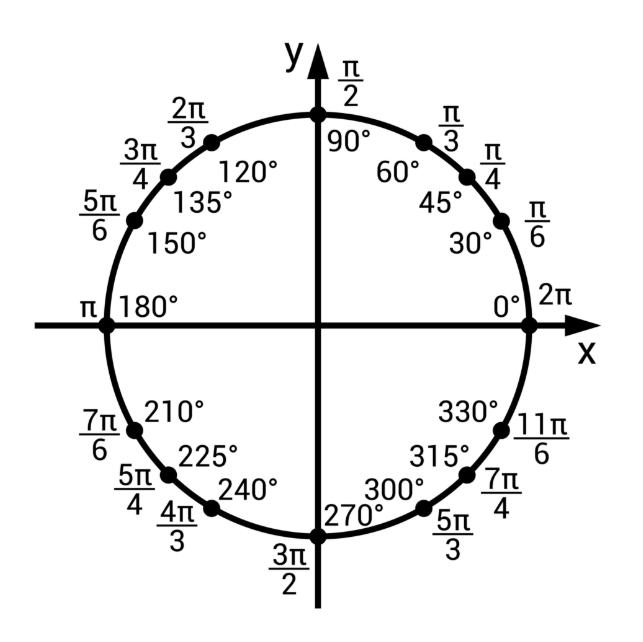
①-1. 単位円と座標への進化
単位円とは、原点 \(\mathbf{(0, 0)}\) を中心とする、半径 \(\mathbf{r=1}\) の円のことです。
この単位円を使うことで、斜辺を常に \(1\) に固定できます。これにより、三角比の値が、座標平面上の点(動径の先端)の座標そのものに進化します。
- 直角三角形の形成: 単位円上の任意の点 \(\text{P}(x, y)\) と原点 \(\text{O}\) を結ぶ線(動径)と \(x\) 軸の正の部分(始線)が作る角を \(\theta\) とします。
- 比率から座標へ: このとき、点 \(\text{P}\) が直角三角形の頂点となり、斜辺の長さは \(1\) です。
| 三角比の定義 | 単位円上の \(\mathbf{r=1}\) の適用 | 結論(座標との一致) |
|---|---|---|
| \(\sin \theta = \displaystyle\frac{\text{対辺}}{\text{斜辺}}\) | \(\sin \theta = \displaystyle\frac{y}{1}\) | \(\mathbf{\sin \theta = y}\) 座標 |
| \(\cos \theta = \displaystyle\frac{\text{隣辺}}{\text{斜辺}}\) | \(\cos \theta = \displaystyle\frac{x}{1}\) | \(\mathbf{\cos \theta = x}\) 座標 |
これにより、サインは縦の長さを、コサインは横の長さを、比率ではなく座標(実際の長さ)として直接表せるようになりました。
\(\tan \theta\) は \(\displaystyle\frac{\text{対辺}}{\text{隣辺}}\) で定義されるため、単位円上では \(\mathbf{\tan \theta = \displaystyle\frac{y}{x}}\) となります。
\(\tan \theta\) は \(\sin \theta\) や \(\cos \theta\) のように座標そのものではないため、上記の表に含めていませんが、この \(\mathbf{\displaystyle\frac{y}{x}}\) の関係は、今後の符号決定や関係式で非常に重要になります。
①-2. 角度の概念の拡張(動径と始線)
単位円を導入することで、角度 \(\theta\) の定義も拡張されます。
- 始線(しせん): 角度を測り始める基準線。\(x\) 軸の正の部分を常に始線とします。
- 動径(どうけい): 角度 \(\theta\) を作る、原点から単位円上の点 \(\text{P}\) へ伸びる線分、つまり単位円の半径 (r) であり、常に \(1\) です。この動径の回転によって角度 \(\theta\) が決まります。
- 正の向きと負の向き: \(\theta\) が反時計回りに測られるときを正の角、時計回りに測られるときを負の角と定義します。
グラフで表現すると、下図の通りです。
※ グラフの作成に GeoGebra を使用しているため、角度が \(\theta\) ではなく \(a\) で表記されています。
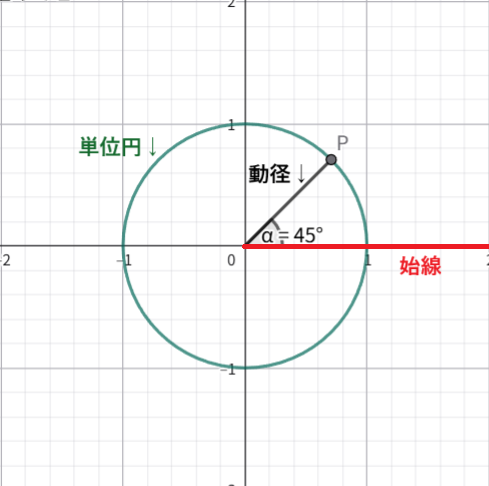
この仕組みにより、\(\mathbf{90^\circ}\) を超える角度(鈍角、負の角など)であっても、動径が止まった位置の座標 \((x, y)\) を読み取るだけで、三角関数を定義できます。
② 角度の符号(象限)と三角関数の値
単位円を導入したことで、角度は \(360^\circ\) や負の角度まで拡張されました。
しかし、動径がどのエリア(象限)にあるかによって、\(\sin, \cos, \tan\) の値の符号(プラスかマイナスか)が変わります。
三角関数の値を決定するには、この符号ルールの理解が不可欠です。
②-1. 象限(しょうげん)と角度の範囲
象限とは、座標平面が \(x\) 軸と \(y\) 軸によって分けられる4つのエリアのことです。
象限は、反時計回り(角度の正の方向)に、第I象限から第IV象限まで番号が付けられています。
- 第I象限: \(x\) 軸、 \(y\) 軸ともに正のエリア。
- 第II象限: \(x\) 軸が負、 \(y\) 軸が正のエリア。
- 第III象限: \(x\) 軸、 \(y\) 軸ともに負のエリア。
- 第IV象限: \(x\) 軸が正、 \(y\) 軸が負のエリア。

角度 \(\theta\) の動径がどの象限に位置するかによって、点 \(\mathbf{P}(x, y)\) の \(x\) 座標と \(y\) 座標の符号が決まります。
②-2. 各象限での三角関数の符号
前のセクション①で確認した通り、
- \(\cos \theta = x\) 座標
- \(\sin \theta = y\) 座標
- \(\tan \theta = \displaystyle\frac{y}{x}\)
であるため、各象限の座標の符号をそのまま当てはめるだけで、三角関数の符号が決まります。
| 象限 | \(\cos \theta = x\) | \(\sin \theta = y\) | \(\tan \theta = y/x\) | 符号がプラスになるのは |
|---|---|---|---|---|
| 第I | + | + | + | 全て |
| 第II | – | + | – | \(\sin\) |
| 第III | – | – | + | \(\tan\) |
| 第IV | + | – | – | \(\cos\) |
③ \(90^\circ\) 以上の特殊角の確認
単位円と象限の概念により、\(\sin 120^\circ\) や \(\cos 150^\circ\) のような鈍角の三角関数の値を求めることができるようになりました。
値そのものは、第1章で学んだ鋭角 (\(\mathbf{30^\circ, 45^\circ, 60^\circ}\)) の知識を使いますが、セクション②で確認した「符号」を適切に付ける必要があります。
③-1. \(180^\circ – \theta\) の関係式(補角)
\(90^\circ\) を超える角度の値を求めるための基本戦略となるのは、動径が作る角 \(\theta\) を、\(x\) 軸から見てどれぐらい離れているか(基準角 \(180^\circ – \theta\))で考えることです。
\(\mathbf{180^\circ}\) から \(\mathbf{\theta}\) を引いた角を基準として、以下の関係が成り立ちます。
\(\mathbf{\sin (180^\circ – \theta) = \sin \theta}\)
\(\mathbf{\cos (180^\circ – \theta) = – \cos \theta}\)
\(\mathbf{\tan (180^\circ – \theta) = – \tan \theta}\)
💡 なぜ \(\sin\) だけ符号が変わらないのか
- \(\sin \theta\) は\(y\) 座標でしたね。角度が \(180^\circ\) までなら、動径は第I象限または第II象限にあります。
- 第I象限でも第II象限でも、\(y\)座標 (= \(\sin \theta\)) は常にプラスです。
したがって、\(\sin\) の値だけは符号が変わらず、常にプラスになります。
一方、\(\cos \theta\)(\(x\) 座標)や \(\tan \theta\) は、第II象限ではマイナスになるため、関係式にマイナスが付きます。
③-2. 鈍角の値を求めてみる
この関係式と、第1章で学んだ特殊角(\(30^\circ, 60^\circ\))を使って、実際に値を求めてみましょう。
【例1: \(\sin 120^\circ\) の値】
- 基準角の特定:
- \(180^\circ – 120^\circ = \mathbf{60^\circ}\)
- 符号の確認:
- \(120^\circ\) は第II象限です。第II象限では \(\sin\) は\(+\)です。
- 値の決定
- \(\sin 120^\circ = \sin 60^\circ = \mathbf{\displaystyle\frac{\sqrt{3}}{2}}\)
【例2: \(\cos 150^\circ\) の値】
- 基準角の特定:
- \(180^\circ – 150^\circ = \mathbf{30^\circ}\)
- 符号の確認:
- \(150^\circ\) は第III象限です。第III象限では \(\cos\) は\(-\)です。
- 値の決定
- \(\cos 150^\circ = -\cos 30^\circ = \mathbf{-\displaystyle\frac{\sqrt{3}}{2}}\)
④ \(180^\circ\) 以上の角度と負の角
前セクションで、\(\mathbf{180^\circ}\) までの角度(鈍角)を扱えるようになりました。
しかし、波の動きを記述するためには、角度を\(180^\circ\) や \(360^\circ\) を超える領域、そして負の領域まで完全に拡張する必要があります。
単位円を使えば、角度は無限に拡張できます。
④-1. \(360^\circ + \theta\) の関係(回転の周期性)
動径が \(360^\circ\)(円を一周)回転すると、動径は元の位置に戻ります。
そのため、\(\sin, \cos, \tan\) の値は、一周回るごとに同じ値を繰り返します。
これを周期性と呼びます。
\(\mathbf{\sin (360^\circ + \theta) = \sin \theta}\)
\(\mathbf{\cos (360^\circ + \theta) = \cos \theta}\)
\(\mathbf{\tan (360^\circ + \theta) = \tan \theta}\)
これは、\(360^\circ\) の倍数(\(720^\circ, -360^\circ\) など)を角度から引いても、三角関数の値は変わらないことを意味します。
【例: \(\cos 420^\circ\) の】
- \(360^\circ\) を引く: \(420^\circ – 360^\circ = \mathbf{60^\circ}\)
- 値の決定: \(\cos 420^\circ = \cos 60^\circ = \mathbf{\displaystyle\frac{1}{2}}\)
④-2. 負の角(\(-\theta\))の関係
角度を時計回りに測った角を、負の角(マイナスの角度)と定義しました。
負の角の三角関数の値は、第IV象限の符号のルール(セクション②)と、動径が \(x\) 軸に対して対称になることから導かれます。
\(\mathbf{\sin (-\theta) = – \sin \theta}\)
\(\mathbf{\cos (-\theta) = \cos \theta}\)
\(\mathbf{\tan (-\theta) = – \tan \theta}\)
なぜ \(\cos\) だけ符号が変わらないのでしょうか。
\(\theta\) と \(-\theta\) は \(x\) 軸に対して対称の位置に動径があります。
動径が上側(\(\theta\))にあっても下側(\(-\theta\))にあっても、\(x\) 座標は同じ値になります。よって、\(\cos\) だけは符号が変わりません。
第1章の練習問題
【問題 1-1】 単位円上の座標の確認(基本)
角度 \(\mathbf{135^\circ}\) の動径が単位円と交わる点 \(\mathbf{P}(x, y)\) の座標を求めなさい。
解答と解説を見る
解答: \(\mathbf{P \left( -\displaystyle\frac{1}{\sqrt{2}}, \displaystyle\frac{1}{\sqrt{2}} \right)}\)
解説:
- 基準角の特定: \(135^\circ\) は \(180^\circ – 135^\circ = \mathbf{45^\circ}\) を基準角とします。
- 符号の確認: \(135^\circ\) は \(\mathbf{90^\circ}\) と \(\mathbf{180^\circ}\) の間にあるため、第II象限です。
- 第II象限では、\(x\) 座標(\(\cos \theta\))はマイナス(-)
- \(y\) 座標(\(\sin \theta\))はプラス(+)
- 値の決定:
- \(\cos 135^\circ = -\cos 45^\circ = -\displaystyle\frac{1}{\sqrt{2}} \quad (\text{x座標})\)
- \(\sin 135^\circ = \sin 45^\circ = \displaystyle\frac{1}{\sqrt{2}} \quad (\text{y座標})\)
【問題 1-2】 象限と符号の確認
以下の問いに答えなさい。
- 角 \(\mathbf{240^\circ}\) の動径は、第何象限に位置しますか?
- \(\mathbf{\tan 240^\circ}\) の符号は、プラス(+)ですか、マイナス(-)ですか?
解答と解説を見る
解答:
- 第III象限
- プラス(+)
解説:
- 象限の特定: \(240^\circ\) は \(\mathbf{180^\circ}\) と \(\mathbf{270^\circ}\) の間に位置するため、第III象限です。
- 符号の決定:
- 第III象限では、\(x\) 座標は、\(y\) 座標ともにマイナス(-)です。
- \(\tan \theta\) の符号は \(\displaystyle\frac{y}{x}\) で決まるため、\(\frac{-}{-} = \mathbf{+}\) となり、プラスです。
【問題 1-3】 角度の拡張の確認
以下の三角関数の値を求めなさい。
- \(\mathbf{\sin (-45^\circ)}\)
- \(\mathbf{\cos 330^\circ}\)
解答と解説を見る
解答:
- \(\mathbf{-\displaystyle\frac{1}{\sqrt{2}}}\)
- \(\mathbf{\displaystyle\frac{\sqrt{3}}{2}}\)
解説:
- \(\mathbf{\sin (-45^\circ)}\) の計算:
- 負の角の公式 \(\mathbf{\sin (-\theta) = -\sin \theta}\) を適用します。
- \(\sin (-45^\circ) = -\sin 45^\circ = \mathbf{-\displaystyle\frac{1}{\sqrt{2}}}\)
- \(\mathbf{\cos 330^\circ}\) の計算:
- \(\mathbf{330^\circ}\) は \(360^\circ\) に \(\mathbf{30^\circ}\) 足りません。\(360^\circ – 330^\circ = 30^\circ\) を基準角とします。
- \(330^\circ\) は第IV象限です。第IV象限では \(\cos\) はプラス(+)です。
- \(\cos 330^\circ = \cos (360^\circ – 30^\circ) = \cos 30^\circ = \mathbf{\displaystyle\frac{\sqrt{3}}{2}}\)
第2章:ラジアンと三角関数のグラフ
第1章で、角度を \(360^\circ\) や負の方向まで拡張し、三角関数(\(\sin, \cos, \tan\))の値を単位円で求める方法を確立しました。
しかし、このままでは角度をグラフで扱うときや、微分・積分といった解析学に進むときに不都合が生じます。
その不都合を解消するのが、本記事の最重要テーマとも言える新たな角度の単位「ラジアン」です。
① ラジアン(弧度法)の定義と必要性
これまで使ってきた「度(\(\mathbf{^\circ}\))」という単位は、円を \(360\) 等分するという人為的に決められた単位(度数法)です。
これに対し、ラジアンは円の性質そのものに基づいた、自然な単位です。
①-1. ラジアンの定義
ラジアン(弧度法)は、「円の半径に対する、弧の長さの比」で角度を定義します。
\(\mathbf{\text{ラジアン (rad)} = \displaystyle\frac{\text{弧の長さ}}{\text{半径}}}\)
特に、半径と弧の長さが等しいときの角度を \(1\) ラジアン (1 rad) と定義します。
\(\mathbf{1 \text{ rad} = \displaystyle\frac{\text{半径(=弧の長さ)}}{\text{半径}} = 1}\)
①-2. ラジアンが不可欠な理由
物理学や解析学においてラジアンが不可欠な理由は、それが純粋な「比率」であり、無次元量(単位を持たない量)として扱えるからです。
- 度数法(\(^\circ\))を使うと、三角関数の導関数(微分)の公式に\(\displaystyle\frac{\pi}{180}\)のような余計な係数が付き、計算が複雑になります。
- ラジアンを使うことで、微分・積分の公式が非常にシンプルになり、自然科学の現象を記述するのに最適です。
\(\mathbf{\displaystyle\frac{d}{dx} (\sin x) = \cos x} \quad \text{(ラジアン使用時)}\)
② ラジアンと度数法の変換
ラジアンの定義 \(\mathbf{\displaystyle\frac{\text{弧の長さ}}{\text{半径}}}\) を、円一周に適用することで、ラジアンと度数法の関係が導かれます。
ラジアンの定義 \(\mathbf{\displaystyle\frac{\text{弧の長さ}}{\text{半径}}}\) を、円一周に適用することで、ラジアンと度数法の関係が導かれます。
②-1. 円一周のラジアン
円一周の弧の長さは円周 \(2\pi r\)、半径は \(r\) です。
\(\mathbf{\text{円一周 (ラジアン)} = \frac{2\pi r}{r} = 2\pi}\)
これにより、次の基本的な関係が確立します。
\(\mathbf{360^\circ = 2\pi \text{ rad}}\)
この両辺を \(\mathbf{2}\) で割った、以下の公式を暗記することが、変換の基本となります。
\(\mathbf{180^\circ = \pi \text{ rad}}\)
②-2. 変換の公式と主要な角度
前述の基本公式 \(\mathbf{180^\circ = \pi \text{ rad}}\) から、ラジアンから度数、度数からラジアンへの変換公式と、主要な角度を導出します。
| 目的 | 公式 |
|---|---|
| 度数 \(\to\) ラジアン | \((度数) \times \displaystyle\frac{\pi}{180^\circ}\) |
| ラジアン \(\to\) 度数 | \((ラジアン) \times \displaystyle\frac{180^\circ}{\pi}\) |
特に、特殊角のラジアン表記は、今後の学習で常に使いますので、ここで確認しておきましょう。
| 度数法 | ラジアン(rad) |
|---|---|
| \(\mathbf{30^\circ}\) | \(\mathbf{\displaystyle\frac{\pi}{6}}\) |
| \(\mathbf{45^\circ}\) | \(\mathbf{\displaystyle\frac{\pi}{4}}\) |
| \(\mathbf{60^\circ}\) | \(\mathbf{\displaystyle\frac{\pi}{3}}\) |
| \(\mathbf{90^\circ}\) | \(\mathbf{\displaystyle\frac{\pi}{2}}\) |
| \(\mathbf{180^\circ}\) | \(\mathbf{\pi}\) |
| \(\mathbf{360^\circ}\) | \(\mathbf{2\pi}\) |
③ 扇形の弧の長さと面積
これまでの数学で扇形の弧の長さや面積を求めるときは、\(displaystyle\frac{\theta}{360^\circ}\) という分数を掛けていました。
中心角 \(\theta\) をラジアンで表すことで、この計算が驚くほど簡単になります。
③-1. ラジアンによる公式の導出
従来の公式をラジアンを使って変形し、シンプルな公式を導出します。
扇形の中心角を \(\theta\) とし、これをラジアン (rad) で表すことで、従来の公式(\(\frac{\theta}{360^\circ}\) を掛ける形式)を以下のように変形できます。
👉 弧の長さ \(L\) は、円周 \(2\pi r\) に \(\displaystyle\frac{\theta}{2\pi}\) を掛けたものです。
\(L = 2\pi r \times \displaystyle\frac{\theta}{2\pi}\)
ここで、\(2\pi\) が打ち消し合い、\(\mathbf{L = r\theta}\) という非常にシンプルな公式が導かれます。
👉 面積 \(S\) は、円の面積 \(\pi r^2\) に \(\frac{\theta}{2\pi}\) を掛けたものです。
\(S = \pi r^2 \times \frac{\theta}{2\pi}\)
ここで、\(\pi\) が打ち消し合い、\(\mathbf{S = \displaystyle\frac{1}{2} r^2 \theta}\) に整理されます。
③-2. ラジアン専用の公式まとめ
中心角 \(\theta\) をラジアンで表す場合の、扇形の弧の長さ \(L\) と面積 \(S\) の公式をあらためて以下にまとめます。
- 弧の長さ \(L\):\(\mathbf{L = r\theta}\)
- 面積 \(S\):\(\mathbf{S = \frac{1}{2} r^2 \theta}\)
さらに、面積 \(S\) の公式は、\(r\theta = L\) の関係を使って、弧の長さ \(L\) を含む形に変形することもできます。
\(\mathbf{S = \displaystyle\frac{1}{2} r L}\)
③-3. 例題
半径 \(r=6\) で、中心角 \(\theta = \displaystyle\frac{\pi}{3} \text{ rad}\) の扇形について、弧の長さ \(L\) と面積 \(S\) を求めてみましょう。
ヒント: ラジアンを用いた扇形の公式 \(\mathbf{L = r\theta}\) と \(\mathbf{S = \displaystyle\frac{1}{2} r^2 \theta}\) をそのまま適用します。
【解答と解説】
ーー 解答 ーー
弧の長さ \(\mathbf{L=2\pi}\)、面積 \(\mathbf{S=6\pi}\)
ーー 解説 ーー
弧の長さ \(L\) の計算:公式 \(\mathbf{L = r\theta}\) に、\(\mathbf{r=6}\) と \(\mathbf{\theta = \displaystyle\frac{\pi}{3}}\) を代入します。
\(L = 6 \times \frac{\pi}{3} = \mathbf{2\pi}\)
面積 \(S\) の計算:公式 \(\mathbf{S = \displaystyle\frac{1}{2} r^2 \theta}\) に、\(\mathbf{r=6}\) と \(\mathbf{\theta = \displaystyle\frac{\pi}{3}}\) を代入します。
\(S = \displaystyle\frac{1}{2} \times 6^2 \times \displaystyle\frac{\pi}{3} = \displaystyle\frac{1}{2} \times 36 \times \frac{\pi}{3}\)
\( = 18 \times \displaystyle\frac{\pi}{3} = \mathbf{6\pi}\)
④ \(\sin\) 関数のグラフの描き方
三角関数のグラフ、特に \(y = \sin \theta\) のグラフは、単位円の \(y\) 座標の動きを、時間軸(\(\theta\) 軸)に沿って展開したものです。
このグラフは「正弦曲線(サインカーブ)」と呼ばれ、波や振動現象を記述する最も基本的な形です。
④-1. グラフの基本要素
\(y = \sin \theta\) のグラフを理解するために、単位円を\(90^\circ\) (\(\frac{\pi}{2}\) rad) ごとに区切り、\(\mathbf{\theta}\)(角度)と \(\mathbf{y}\)(\(\sin\) の値)の関係を追跡します。
| 角度 \(\theta\) (rad) | \(\sin \theta\) の値 (\(y\) 座標) | 単位円上の \(y\) 座標の動き |
|---|---|---|
| \(\mathbf{0}\) | \(\mathbf{0}\) | \(0\) からスタート |
| \(\mathbf{\displaystyle\frac{\pi}{2}}\) | \(\mathbf{1}\) | \(0 \to 1\) (最大値) |
| \(\mathbf{\pi}\) | \(\mathbf{0}\) | \(1 \to 0\) |
| \(\mathbf{\displaystyle\frac{3}{2}\pi}\) | \(\mathbf{-1}\) | \(0 \to -1\) (最小値) |
| \(\mathbf{2\pi}\) | \(\mathbf{0}\) | \(-1 \to 0\) (一周して元に戻る) |
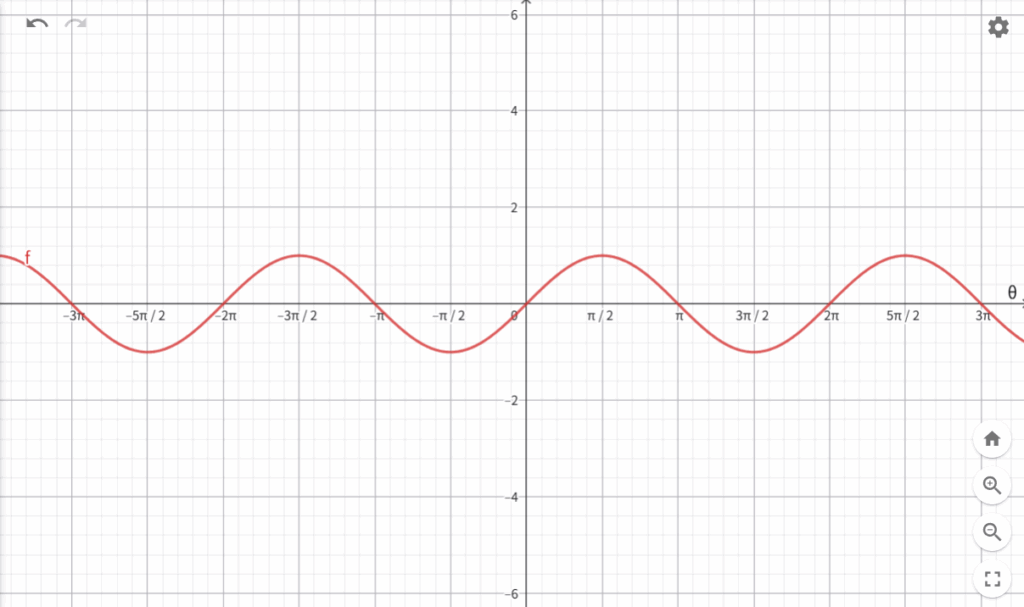
④-2. グラフの特性
このグラフを \(x\) 軸に \(\theta\)(ラジアン)、\(y\) 軸に \(\sin \theta\) の値を取って描くと、以下の特性を持つ波形となります。
| 特性 | 定義 | \(y = \sin \theta\) の値 |
|---|---|---|
| 周期 | グラフが同じ形を繰り返すための角度 | \(\mathbf{2\pi}\) |
| 値域 | \(y\) 座標(\(\sin \theta\) の値)が取りうる範囲 | \(\mathbf{-1 \le y \le 1}\) |
| 最大値 | \(\mathbf{1}\) (\(\theta = \frac{\pi}{2}, \frac{5}{2}\pi, \dots\) で取る) | |
| 最小値 | \(\mathbf{-1}\) (\(\theta = \frac{3}{2}\pi, \frac{7}{2}\pi, \dots\) で取る) |
④-3. 例題
\(y = \sin \theta\) のグラフにおいて、\(\theta\) が \(\mathbf{0}\) から \(\mathbf{4\pi}\) までの区間で、\(\mathbf{y = 0}\) となる \(\theta\) の値をすべて求めてみましょう。
ヒント: \(\mathbf{\sin \theta = y}\) 座標が \(\mathbf{0}\) になる点を、単位円上で特定します。周期 \(2\pi\) を考慮します。
【解答と解説】
ーー 解答 ーー
\(\mathbf{\theta = 0, \pi, 2\pi, 3\pi, 4\pi}\)
ーー 解説 ーー
- 単位円上での特定:\(\sin \theta\) は単位円上の \(y\) 座標なので、\(y=0\) となるのは、動径が \(x\) 軸上に来るときです。それは\(\theta = 0\) と \(\theta = \pi\) の2箇所です。
- 区間内の値:\(\mathbf{0 \le \theta \le 4\pi}\) の区間内で、上記の点を通る角度を \(2\pi\) の周期で探します。
- 1周目: \(\mathbf{0, \pi}\)
- 2周目: \(0+2\pi = \mathbf{2\pi}\), \(\pi+2\pi = \mathbf{3\pi}\)
- 周目: \(4\pi\) も区間に含まれます。
- すべての値:したがって、\(\mathbf{0, \pi, 2\pi, 3\pi, 4\pi}\) です。
⑤ \(\cos\) 関数のグラフ
\(y = \cos \theta\) のグラフ(余弦曲線、コサインカーブ)は、\(y = \sin \theta\) のグラフと非常に似ています。単位円では、\(\cos \theta\) は動径の\(x\) 座標で定義されていました。
⑤-1. \(\cos\) グラフの基本要素
\(\sin\) グラフと同様に、単位円の \(x\) 座標の動きを \(\theta\) 軸に展開することで、グラフが描けます。
| 角度 \(\theta\) (rad) | \(\cos \theta\) の値 (\(x\) 座標) | 単位円上の \(x\) 座標の動き |
|---|---|---|
| \(\mathbf{0}\) | \(\mathbf{1}\) | \(1\) からスタート (最大値) |
| \(\mathbf{\displaystyle\frac{\pi}{2}}\) | \(\mathbf{0}\) | \(1 \to 0\) |
| \(\mathbf{\pi}\) | \(\mathbf{-1}\) | \(0 \to -1\) (最小値) |
| \(\mathbf{\displaystyle\frac{3}{2}\pi}\) | \(\mathbf{0}\) | \(-1 \to 0\) |
| \(\mathbf{2\pi}\) | \(\mathbf{1}\) | \(0 \to 1\) (一周して元に戻る) |
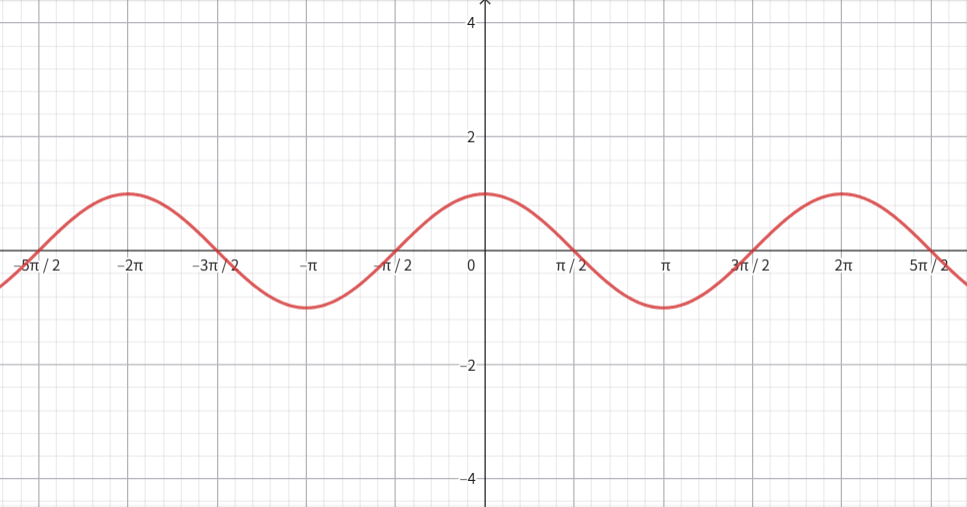
⑤-2. \(\sin\) グラフとの関係(平行移動)
\(\cos\) グラフは、\(\sin\) グラフを\(x\) 軸方向に \(\mathbf{-\frac{\pi}{2}}\) だけ平行移動(グラフ全体を左に \(\mathbf{\frac{\pi}{2}}\) ずらす)したものと完全に一致します。
これは、以下の関係式によって数学的に裏付けられます。
\(\mathbf{\cos \theta = \sin \left( \theta + \frac{\pi}{2} \right)}\)
したがって、\(\cos\) グラフも \(\sin\) グラフと同じ周期 (\(\mathbf{2\pi}\)) と同じ値域 (\(\mathbf{-1 \le y \le 1}\)) を持ちます。
⑤-3. 例題
\(y = \cos \theta\) のグラフにおいて、\(\theta\) が \(\mathbf{0}\) から \(\mathbf{2\pi}\) までの区間で、最大値を取る \(\theta\) の値をすべて求めてみましょう。
ヒント: \(\mathbf{\cos \theta = x}\) 座標が最大値 \(\mathbf{1}\) になる点を、単位円上で特定します。
【解答と解説】
ーー 解答 ーー
\(\mathbf{\theta = 0, 2\pi}\)
ーー 解説 ーー
- 単位円上での特定:\(\cos \theta\) は単位円上の \(x\) 座標なので、最大値 \(\mathbf{1}\) となるのは、動径が\(x\) 軸の正の部分に来るときです。
- 区間内の値:\(\mathbf{0 \le \theta \le 2\pi}\) の区間内で、最大値を取る角度は、\(\theta = 0\) と、一周回った\(\theta = 2\pi\) です。
⑥ \(\tan\) 関数のグラフと漸近線
\(y = \tan \theta\) のグラフは、\(\sin\) や \(\cos\) のような連続した波形ではなく、無限に伸びる直線(漸近線)で区切られた特異な形状をしています。
⑥-1. 定義されない角度と漸近線
\(\tan \theta\) は、セクション①で確認した通り、\(\mathbf{\tan \theta = \frac{y}{x} = \frac{\sin \theta}{\cos \theta}}\)で定義されます。
\(\cos \theta\)(\(x\) 座標)が \(0\) になる角度では、分母が \(0\) になるため、\(\tan \theta\) の値は定義されません。
この「定義されない角度」の前後で、\(\tan \theta\) の値は正・負の無限大へと急激に変化します。このとき、グラフが限りなく近づく垂直な直線が漸近線となります。
一般に、漸近線の方程式は、\(\mathbf{\theta = \frac{\pi}{2} + n\pi}\)(\(n\) は整数)となります。
⑥-2. \(\tan\) グラフの特性
\(\tan\) グラフは、漸近線によって区切られた区間で、無限に伸びる波形を繰り返します。
| 特性 | 定義 | \(y = \tan \theta\) の値 |
|---|---|---|
| 周期 | グラフが同じ形を繰り返すための角度 | \(\mathbf{\pi}\) |
| 値域 | \(y\) 座標が取りうる範囲 | すべての実数 (\(\mathbf{-\infty < y < \infty}\)) |
| 漸近線 | グラフが限りなく近づく直線 | \(\mathbf{\theta = \frac{\pi}{2} + n\pi}\) |
第3章:量子力学で必須の数学「オイラーの公式」と「複素数」
これまでの三角関数の学習は、すべてこのオイラーの公式(Euler’s formula)を理解するための準備(序章)だったと言えます。
量子力学では、波の運動を記述するために、実数の拡張である複素数を使います。
① 虚数と複素数の定義
①-1. 虚数単位 \(\mathbf{i}\) の導入
「虚数」とは、実数(\(0, 1, -2, \sqrt{3}\) など)の範囲には存在しない、仮想の数です。
虚数は、2乗すると \(\mathbf{-1}\) になる数として定義され、これを虚数単位 \(\mathbf{i}\) と呼びます。
\(\mathbf{i^2 = -1 \quad \text{または} \quad i = \sqrt{-1}}\)
①-2. 複素数の定義
複素数(complex number)とは、実数 \(a\) と \(b\) を使って、実数部と虚数部を組み合わせた、以下のような形式で表される数です。
\(\mathbf{z = a + bi}\)
- 実数部 (Real Part):\(\mathbf{a}\)
- 虚数部 (Imaginary Part):\(\mathbf{bi}\)
複素数は、数直線(一次元)ではなく、後述する複素平面(二次元)の上で点を表します。
この二次元的な表現が、波や回転を扱う量子力学で極めて重要になります。
①-3. 複素平面(ガウス平面)
複素平面(complex plane)はガウス平面(Gaussian plane)とも呼ばれ、複素数 \(\mathbf{z = a + bi}\) を幾何学的に扱うために、実数軸と虚数軸の2つの軸で構成される平面のことです。
複素平面では、横軸を実軸(実数 \(a\) を表す軸)、縦軸を虚軸(虚数 \(bi\) を表す軸)として、複素数 \(z = a + bi\) を座標 \(\mathbf{(a, b)}\) の点として表現します。
\(\mathbf{i}\) は「実在しない数」ですが、複素平面では \(\mathbf{i}\) は「実軸から \(90^\circ\) 回転しなさい」という方向の性質を示す記号として扱われます。
したがって、縦軸(虚軸)にプロットするのは、虚数 \(bi\) の「実数的な大きさ」である \(\mathbf{b}\) です。
複素数 \(\mathbf{z}\) は、「実数の部分 \((\mathbf{a})\)」と「虚数方向への実数的な長さ \((\mathbf{b})\)」という二つの実数の組 \((\mathbf{a}, \mathbf{b})\) によって、平面上の点として完全に表現されます。
これにより、複素数は「原点からの距離(大きさ)」と「実軸からの角度(偏角)」という、極座標の形で表すことができるようになります。
💡極座標とは
これまで慣れ親しんだ座標 \((\mathbf{x}, \mathbf{y})\) は直交座標(デカルト座標)と呼ばれます。
これに対し、極座標とは、点を「原点からの距離 \(\mathbf{r}\)」と「角度 \(\mathbf{\theta}\)」の組 \(\mathbf{(r, \theta)}\) で表す座標系のことです。
複素平面では、この極座標で表現することが、波の回転や位相を扱う上で圧倒的に有利になります。
② 複素数の極形式(三角関数形式)
複素数 \(\mathbf{z = a + bi}\) を、実軸と虚軸で表す直交座標 \(\mathbf{(a, b)}\) から、原点からの距離 \(r\) と 実軸からの角度 \(\theta\) で表す極座標 \(\mathbf{(r, \theta)}\) へと変換した表現を極形式と呼びます。
この形式は、複素数の掛け算が「回転」を意味することを示唆しており、波の位相変化を扱う量子力学で必須となります。
②-1. 極形式の導出
複素平面上の点 \(z = a + bi\) を考えます。
- 実数部 \(a\) と虚数部 \(b\) の三角関数による表現:
- 距離 \(r\) と偏角 \(\theta\) を使うと、定義より \(a = r \cos \theta\) と \(b = r \sin \theta\) が成り立ちます。
- 極形式への変形:元の式 \(z = a + bi\) に代入します。
- \(z = r \cos \theta + (r \sin \theta) i\)
- \(z = \mathbf{r (\cos \theta + i \sin \theta)}\)
この \(\mathbf{z = r (\cos \theta + i \sin \theta)}\) が複素数の極形式です。
極形式を構成する絶対値 \(\mathbf{r}\) と偏角 \(\mathbf{\theta}\) は、直交座標 \((\mathbf{a}, \mathbf{b})\) を用いて、以下のように定義・計算されます。
\(\mathbf{r}\):絶対値(原点からの距離)の導出は次の式👇
\(r = \sqrt{a^2 + b^2}\)
\(\mathbf{\theta}\):偏角(実軸からの角度)の導出は次の式👇
\(\tan \theta = \displaystyle\frac{b}{a}\)
💡 量子力学との対応
極形式は、量子力学の波動関数を理解する上で、以下のように重要な物理的概念と対応します。
- 絶対値 \(r\): 波動関数における振幅(波の大きさ)に対応します。
- 偏角 \(\theta\): 波動関数における位相(波の回転角)に対応します。
②-2. 例題
複素数 \(\mathbf{z = 1 + i}\) を極形式で表してみましょう。
ヒント: まず \(r\)(絶対値)を求め、次に \(\theta\)(偏角)を求めます。
【解答と解説】
ーー 解答 ーー
\(\mathbf{z = \sqrt{2} \left( \cos \displaystyle\frac{\pi}{4} + i \sin \displaystyle\frac{\pi}{4} \right)}\)
ーー 解説 ーー
- 絶対値 \(r\) の計算: \(a=1, b=1\) より、
- \(r = \sqrt{1^2 + 1^2} = \mathbf{\sqrt{2}}\)
- 偏角 \(\theta\) の計算: \(\tan \theta = \displaystyle\frac{b}{a} = \displaystyle\frac{1}{1} = 1\)
- \(1+i\) は第I象限にあるため、 \(\theta\) は \(\mathbf{45^\circ}\) または \(\mathbf{\displaystyle\frac{\pi}{4} \text{ rad}}\) です。
したがって、極形式は \(\mathbf{z = \sqrt{2} \left( \cos \frac{\pi}{4} + i \sin \displaystyle\frac{\pi}{4} \right)}\) となります。
③ オイラーの公式(Euler’s Formula)
セクション②で、複素数を極形式 \(\mathbf{z = r (\cos \theta + i \sin \theta)}\) で表すことを学びました。
オイラーの公式は、この \(\mathbf{\cos \theta + i \sin \theta}\) という部分を、\(\mathbf{e^{i\theta}}\)という指数関数の形でシンプルに書き換える公式です。
③-1. オイラーの公式の定義
オイラーの公式は、ネイピア数 \(\mathbf{e}\)(自然対数の底、約 2.718)と、虚数単位 \(\mathbf{i}\)、そして角度 \(\mathbf{\theta}\) を結びつける、以下の数式です。
\(\mathbf{e^{i\theta} = \cos \theta + i \sin \theta}\)
この公式は、極形式に適用すると、複素数 \(z\) を以下のように最も簡潔な指数形式で表現することを可能にします。
\(\mathbf{z = r e^{i\theta}}\)
💡 公式の持つ意味:回転と波動
オイラーの公式の最大の価値は、「指数関数」が「三角関数(波と振動)」と「虚数 \(\mathbf{i}\)(90°回転)」という、まったく異なる要素を完全に統合している点にあります。
- \(\mathbf{e^{i\theta}}\) の幾何学的意味:\(\mathbf{r=1}\) の場合、\(\mathbf{e^{i\theta}}\) は、単位円上を角度 \(\mathbf{\theta}\) に応じて反時計回りに回転する点を示します。
💡 指数法則と位相の変化
指数法則 \(\mathbf{(e^{i\alpha} \cdot e^{i\beta} = e^{i(\alpha+\beta)})}\) は、複素数の掛け算が回転(角度の足し算)を意味することを示しており、波動の位相の変化を扱うのに最適です。
③-2. 量子力学との関係:波動関数 \(\mathbf{\Psi}\)
量子力学では、粒子の状態を記述する波動関数 \(\mathbf{\Psi}\) は、ほとんどの場合、オイラーの公式を含む指数関数の形で表現されます。
例えば、時間に依存する自由粒子の波動関数は、しばしば以下の形を持ちます。
\(\mathbf{\Psi (x, t) \propto e^{i(kx – \omega t)}}\)
この関数は、オイラーの公式を使って展開すると、\(\cos\) と \(\sin\) を含む「波の形」になります。
\(\mathbf{e^{i(kx – \omega t)}} = \mathbf{\cos(kx – \omega t) + i \sin(kx – \omega t)}\)
このように、オイラーの公式を用いることで、量子力学の波の解析が極めて簡潔になり、微分・積分といった計算も容易になります。
③-2. 例題
オイラーの公式を用いて、複素数 \(\mathbf{z = 1 + i}\)(セクション②の例題)を指数形式で表してみましょう。
ヒント: セクション②で求めた絶対値 \(\mathbf{r}\) と偏角 \(\mathbf{\theta}\) の値を、指数形式の公式 \(\mathbf{z = r e^{i\theta}}\) に代入するだけです。
【解答と解説】
ーー 解答 ーー
\(\mathbf{z = \sqrt{2} e^{i \displaystyle\frac{\pi}{4}}}\)
ーー 解説 ーー
- 極形式の確認(セクション②より)、
- \(z = \sqrt{2} \left( \cos \displaystyle\frac{\pi}{4} + i \sin \displaystyle\frac{\pi}{4} \right)\)
- オイラーの公式の適用: オイラーの公式 \(\mathbf{e^{i\theta} = \cos \theta + i \sin \theta}\) において、\(\mathbf{\theta = \displaystyle\frac{\pi}{4}}\) であるため、
- \(\mathbf{\cos \displaystyle\frac{\pi}{4} + i \sin \displaystyle\frac{\pi}{4} = e^{i \displaystyle\frac{\pi}{4}}}\)
- 指数形式への変換: これを極形式に代入し、指数形式 \(\mathbf{z = r e^{i\theta}}\) とします。
- \(z = \mathbf{\sqrt{2} e^{i \frac{\pi}{4}}}\)
まとめ
本記事で学んだ「三角関数」、「ラジアン」、そして「オイラーの公式」は、量子力学の波動関数 \(\mathbf{\Psi}\) を理解し、計算するための必要不可欠な数学の土台です。
量子力学では、電子などの粒子の振る舞いを記述する際に、以下の3つのコアな概念が結びつきます。
- 角度の単位:ラジアンの絶対的必要性
- 知識:\(\mathbf{180^\circ = \pi \text{ rad}}\)
- 役割:物理学で波や回転を微分・積分する際、角度の単位は常にラジアンでなければなりません。度数法(\(360^\circ\))は計算が複雑になるため、量子力学の数式に登場することはありません。
- 波の実体:\(\mathbf{\sin}\) と \(\mathbf{\cos}\) の周期性
- 知識:\(\mathbf{\sin}\) と \(\mathbf{\cos}\) の周期 \(\mathbf{2\pi}\) と値域 \(\mathbf{-1 \le y \le 1}\)
- 役割:波動関数 \(\mathbf{\Psi}\) が空間や時間に対して振動する波であること、そしてその波の周期的な性質(振動)を理解するための、最も直感的なモデルとなります。
- 波動関数の心臓部:オイラーの公式 \(\mathbf{e^{i\theta}}\)
- 知識:\(\mathbf{e^{i\theta} = \cos \theta + i \sin \theta}\)
- 役割:波動関数は複素数の波であり、その複素数の波を最も扱いやすくする表現が、指数形式 \(\mathbf{e^{i\theta}}\) です。
\(\mathbf{e^{i\theta}}\) の幾何学的な意味は、単位円上の「回転(位相)」です。量子力学では、粒子の状態変化や時間の経過に伴う波の変化を、この「指数関数による回転」として解析します。
次なるステップへ
これまでの『大人の学び直し数学』シリーズを通じて、以下の数学的土台を完成させました。
- 代数計算の基礎(展開、平方完成)
- 三角関数とオイラーの公式(波・回転の捉え方)
これらの知識は、シュレーディンガー方程式(量子力学の根幹をなす方程式)を理解し、実際に解いていく上で非常に重要です。
量子力学では、波の「変化」や多次元空間を扱うため、「微分・積分」や「線形代数」の知識も欠かせないものです。
しかし、これらの知識は、量子力学の学習を進めながら、必要に応じて補完していくことが十分に可能です。
数学的な準備は整いました。
いよいよ量子力学の本編へと、歩みを進めていきましょう。



コメント