これまでの『量子プログラミングシリーズ【入門編】』を通じて、私たちはQiskitを使い、量子ビットの重ね合わせや量子もつれといった基礎的な現象をコードで体験してきました。
シミュレーターでのノイズ体験や、IBMの実機へのシンプルなジョブ送信にも挑戦し、量子コンピューティングが理論だけでなく、現実の物理現象に基づいていることを深く理解していただけたかと思います。
そして、今回からはいよいよ『実践編』として、本格的な量子アルゴリズムの実装に挑戦し始めます。
私たちが最終的に知りたいのは、「量子コンピューターは、従来の古典コンピューターと比べて具体的に何がすごいのか?」という核心ではないでしょうか。
その疑問に対し、優位性の存在をシンプルかつ劇的に証明した歴史的なアルゴリズムの一つが「ドイッチュ・ジョサのアルゴリズム」です。
本記事では、入力ビット数 n=4 という極小の回路を用いて量子優位性をQiskitで実装し、その決定的な差をコードと実行結果で証明します。
目次
第1章:ドイッチュ・ジョサが解決する古典的な難題
ドイッチュ・ジョサのアルゴリズムは、量子アルゴリズムであり、1992年にデイビッド・ドイッチュ(英語版)とリチャード・ジョサ(英語版)によって提案され、 Richard Cleve, アーター・エカート, Chiara Macchiavello, そして Michele Mosca によって 1998 年に改良された。
引用元Wikipedia:https://ja.wikipedia.org/wiki/%E3%83%89%E3%82%A4%E3%83%83%E3%83%81%E3%83%A5%E3%83%BB%E3%82%B8%E3%83%A7%E3%82%B5%E3%81%AE%E3%82%A2%E3%83%AB%E3%82%B4%E3%83%AA%E3%82%BA%E3%83%A0
① 古典的な「難問」:定数関数か、バランス関数か
ドイッチュ・ジョサのアルゴリズムが挑む課題は、ある未知の関数 \(f(x)\) が与えられたとき、その関数が以下のどちらのタイプであるかを判別することです。
- 定数関数(Constant Function): 全ての入力 \(x\) に対して、出力が常に同じ値(0または1)になる関数です。 \(f(x) = 0\) または \(f(x) = 1\)
- バランス関数(Balanced Function): 全ての入力 \(x\) のうち、ちょうど半数が 0 を出力し、残り半数が 1 を出力する関数です。
このシンプルな判定が、なぜ量子コンピューターにとって「優位性を示す課題」となるのでしょうか。
①-1. 古典コンピューターが抱える決定的な限界
本記事で作成するデモプログラムでは、入力ビット数を \(\boldsymbol{n=4}\) とします。
これにより、関数 \(f(x)\) には \(N=2^4 = 16\) 通りの入力パターンが存在します。
古典的なコンピューターがこの \(f(x)\) を確実に判定しようとすると、最悪のケースで \(\mathbf{9 \text{回}}\) もの関数への問い合わせ(クエリ)が必要になります。
この \(9 \text{回}\) という回数は、入力が増えるほど \(2^{n-1} + 1\) の指数関数的なペースで増大します。
ドイッチュ・ジョサのアルゴリズムは、この古典的な限界を、たった1回のクエリで打ち破ります。
② 量子的な突破口:重ね合わせとオラクル
ドイッチュ・ジョサのアルゴリズムが、古典コンピューターの壁(9回のクエリ)を、たった1回のクエリで打ち破る鍵は、量子コンピューティングの二つの基本原理にあります。
②-1. 「オラクル」とは何か?(ブラックボックスの力)
量子アルゴリズムでいうオラクル(Oracle)とは、古典的な関数 \(f(x)\) の計算ルールを量子回路(量子ゲートの組み合わせ)で実装したブラックボックスのことです。
アルゴリズムの論理(ドイッチュ・ジョサの本体)は、このオラクルの内部構造には一切関心を持ちません。
重要なのは、「このブラックボックスに何回問い合わせたか(クエリ回数)」という点だけです。
古典コンピューターが \(f(x)\) の計算に \(2^{n-1} + 1\) 回のクエリを必要とするのに対し、量子コンピューターはこのオラクルにたった1回だけクエリを投げかけます。
②-2. 量子並列性(重ね合わせの力)
まず、Hゲート(アダマールゲート)を使って、入力となる \(\boldsymbol{n=4}\) の量子ビット全てを重ね合わせ状態にします。
この操作により、量子ビットは \(\boldsymbol{0000}\) から \(\boldsymbol{1111}\) までの16通りの全ての入力パターンを同時に表現します。
\(|\psi_{in}\rangle = \displaystyle\frac{1}{\sqrt{16}}(|0000\rangle + |0001\rangle + \dots + |1111\rangle)\)
この状態を、古典的な関数 \(f\) を量子回路として実装したオラクルに投入することで、1回の操作で16通りの計算を並列に実行します。
これが量子並列性です。
②-3. 位相キックバック(オラクルと干渉の仕組み)
ただ計算を並列に行うだけでは、測定時に全ての計算結果が混ざってしまい、定数かバランスかの情報を取り出せません。
そこで、オラクルに投入する出力量子ビットを、事前に \(\boldsymbol{|-\rangle}\) 状態(\(|0\rangle\) と \(|1\rangle\) の特定の重ね合わせ)に準備します。
この \(\boldsymbol{|-\rangle}\) 状態は、計算結果 \(f(x)\) に応じて、入力量子ビットの位相(波のズレ)に変化をもたらします。
この現象を位相キックバックと呼びます。
- 定数関数の場合:全ての入力パターンで位相の変化量が同じになります。
- バランス関数の場合:入力の半分(8パターン)で位相の変化方向が逆になります。
この位相の変化が、関数 \(f\) の情報であり、後のステップで「定数」と「バランス」を判別するための決定的な痕跡となります。
③ 判定の仕組み:最終測定と干渉
重ね合わせ状態と位相キックバックによってオラクルを通過した量子状態は、既に「定数」か「バランス」かの情報を位相の中に保持しています。
しかし、この情報は直接測定しても取り出すことができないのです。
③-1. 最終アダマールゲートによる干渉
情報を引き出すために、最後の仕上げとして、入力量子ビット全てにHゲート(アダマールゲート)を再度適用します。
この最後のHゲートは、ドイッチュ・ジョサの鍵となる操作です。
位相の変化の情報を振幅(測定確率)に変換することで、「定数」か「バランス」かの二択を明確に分離します。
- 定数関数の場合:Hゲート適用後、位相の変化がなかった \(\boldsymbol{|0000\rangle}\) の振幅が増幅され、測定結果は \(\boldsymbol{0000}\) に集中します。
- バランス関数の場合:Hゲート適用後、位相が打ち消し合っていた \(\boldsymbol{|0000\rangle}\) の振幅が完全に相殺され、測定結果は \(\boldsymbol{0000}\) 以外の状態に集中します。
バランス関数と判定された場合、測定結果は \(\boldsymbol{0000}\) 以外の \(\boldsymbol{15}\) 通り、つまり下記のいずれか一つに集中します。
0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111
ただし、どの状態になるかは、オラクルとして使用した関数の性質(本記事のプログラムで使用するのはXOR演算)によって理論的に決まります。
本記事のプログラムではオラクルにXOR演算を使用しており、実装する \(f(x) = x_1 \oplus x_2 \oplus x_3 \oplus x_4\) の場合、測定結果は15通りのいずれかではなく、必ず \(\boldsymbol{1111}\) になることが確定しています。
③-2. 測定結果と判定基準
最終的に、入力量子ビットを測定することで、関数 \(f\) のタイプが100%の確率で確定します。
| 最終的な測定結果 | 判定される関数 \(f\) のタイプ |
|---|---|
0000 に集中 | 定数関数である |
0000 以外に集中 | バランス関数である |
この「測定結果が \(\boldsymbol{0000}\) であるかどうか」という二択で、古典では9回必要な判定を、量子はたった1回のクエリで達成します。
第2章:ドイッチュ・ジョサ回路の全貌
① 回路を構成する5つのステップ
ドイッチュ・ジョサのアルゴリズムは、量子並列性と干渉(位相キックバック)という強力な仕組みを駆使しながらも、その判定をわずか5つの主要なステップという極めて簡潔な構成で実現しています。
このアルゴリズムは、入力ビット数(\(n\))や、判定する定数/バランス関数の種類が変わっても、その論理的な構造は不変です。
| ステップ | 目的 | 実施するゲート | 役割 |
|---|---|---|---|
| 1 | 出力ビットの準備 | \(X\) ゲートと \(H\) ゲート | 位相キックバックを起こすための \(\boldsymbol{|-\rangle}\) 状態を準備する。 |
| 2 | 入力ビットの重ね合わせ | \(H\) ゲート(全入力に適用) | 全ての入力パターンを量子並列性で同時に処理できる状態にする。 |
| 3 | オラクル \(U_f\) の適用 | 関数 \(f\) の量子回路 | 1回のクエリで、関数の情報を位相に書き込む(量子優位性の核心)。 |
| 4 | 最終干渉 | \(H\) ゲート(全入力に再度適用) | 位相情報を測定可能な振幅(確率)へと変換する。 |
| 5 | 測定 | 測定ゲート | 最終結果(定数 \(0000\) か、バランス \(\neq 0000\) か)を確定させる。 |
上記5つのステップを、次のセクション②で構築する回路図と照らし合わせながら、順を追って詳しく解説していきます。
② 回路図の設計と実装の準備
ここからは、実際にQiskitで実装する \(\boldsymbol{n=4}\) のドイッチュ・ジョサ回路をイメージしながら、先ほどの5つのステップを量子ビットの操作に落とし込んでいきます。
②-1. 量子ビットと古典ビットの構成
今回構築する回路は、入力量子ビット \(n=4\) に、オラクル用の出力量子ビット \(1\) 個を加えた合計 \(5\) 量子ビットで構成されます。
測定結果を記録するために、入力量子ビットと同数の \(4\) 古典ビットを使用します。
- 入力量子ビット (q[0]~q[3]): 4ビット。測定の結果を受け取る。
- 出力量子ビット (q[4]): 1ビット。オラクル操作に使用される。
- 古典ビット (c[0]~c[3]): 4ビット。入力量子ビットの測定結果を記録する。
②-2. 回路図と各ステップのゲート操作
回路図は、5つのステップが直列につながったシンプルな形になります。
| ステップ | ゲート操作 | 対象ビット | 役割 |
|---|---|---|---|
| 1 | \(X\) ゲート, \(H\) ゲート | q[4] | 位相キックバックを起こすための \(\boldsymbol{|-\rangle}\) 状態を準備する。 |
| 2 | \(H\) ゲート | q[0]~q[3] | 入力ビットを重ね合わせ状態にし、量子並列性を確立。 |
| 3 | オラクル \(U_f\) | q[0]~q[4] | (※1)関数 \(f\) に応じたCNOTゲートなどを適用。 |
| 4 | \(H\) ゲート | q[0]~q[3] | 位相情報を測定確率に変換する最終干渉。 |
| 5 | 測定 | q[0]→c[0], \(\dots\), q[3]→c[3] | 最終的な結果を古典ビットに記録。 |
③ Qiskitコードで回路の共通構造を構築
いよいよ、これまでに解説した5つのステップをQiskitコードで実装します。
ドイッチュ・ジョサの構造は不変であるため、まずはオラクル(Step 3)を除く共通部分を関数として定義します。
以降の実装は、VS Codeでの開発環境がすでに構築されていることを前提に解説を進めます。
環境構築がお済みでない方は、先にシリーズの【入門編】第1回記事にて環境設定(第2章まで)を完了させてから、本記事に戻っていただくようお願いいたします。
③-1. Qiskitによる共通回路の構築
以下の関数 create_deutsch_jozsa_circuit は、オラクル関数を引数として受け取ります。
定数とバランスのオラクルを簡単に切り替えることを可能にするためです。
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit import transpile
# 他の必要なライブラリも適宜インポートが必要です
def create_deutsch_jozsa_circuit(num_qubits, oracle_func):
"""
ドイッチュ・ジョサ回路の共通構造を構築する関数。
n=4の場合、num_qubitsは4。合計5量子ビットを使用する。
"""
# 5量子ビット (q[0]~q[4]) と 4古典ビット (c[0]~c[3]) を定義
qr = QuantumRegister(num_qubits + 1, name='q')
cr = ClassicalRegister(num_qubits, name='c')
qc = QuantumCircuit(qr, cr)
input_qubits = qr[:num_qubits] # q[0]~q[3]
output_qubit = qr[num_qubits] # q[4]
# --- Step 1: 出力ビットの準備 (|-\rangle 状態への初期化) ---
qc.x(output_qubit) # |0\rangle -> |1\rangle
qc.h(output_qubit) # |1\rangle -> |-\rangle
# --- Step 2: 入力ビットの重ね合わせ ---
qc.h(input_qubits) # 全ての入力ビットを重ね合わせ状態にする
qc.barrier()
# --- Step 3: オラクル Uf の適用 (★ここは外部から受け取る) ---
oracle_func(qc, input_qubits, output_qubit)
qc.barrier()
# --- Step 4: 最終干渉 (再重ね合わせ) ---
qc.h(input_qubits)
qc.barrier()
# --- Step 5: 測定 ---
# q[0]~q[3] の測定結果を c[0]~c[3] に記録
qc.measure(input_qubits, cr)
return qc③-2. 構造の確認
このコードは、前のセクションで確認したStep 1, 2, 4, 5を忠実に再現しています。
特に、量子優位性の核心であるオラクルの適用(Step 3)を、引数 oracle_func として受け取り、内部で実行する仕様で実装しており、定数とバランスの両方の判定に使える汎用性を持たせています。
第3章:オラクルの核心部分を実装
① 定数オラクル(\(f(x)=0\))の実装
オラクル(Step 3)は、関数 \(f(x)\) の計算ルールを量子回路で実装したものです。
最も簡単な定数関数である \(f(x)=0\) の場合を考えます。
この関数は、入力 \(x\) が何であっても、出力は常に \(0\) です。
量子回路の操作に直すと、「入力量子ビット \(q[0] \sim q[3]\) の状態によらず、出力量子ビット \(q[4]\) の状態を変化させない」ということになります。
①-1. 何もしないのが最適解
量子回路において、何もしない操作は恒等操作(Identity Operation)と呼ばれ、最もシンプルなゲート操作です。
\(U_f (|x\rangle |q_4\rangle) = |x\rangle |q_4 \oplus 0\rangle = |x\rangle |q_4\rangle\)
したがって、定数オラクル \(f(x)=0\) の実装は、出力ビット \(q[4]\) に対して一切のゲート操作を加えないことが最適解となります。
①-2. Qiskitコードによる実装
# === 1. オラクル定義関数 A: 定数関数 f(x)=0 ===
def oracle_constant_zero(qc, input_qubits, output_qubit):
"""
定数関数 f(x)=0 を実装するオラクル。
入力量子ビットの状態に関わらず、出力量子ビットを変化させない(何もしない)。
"""
# f(x)=0 の場合、恒等操作となるためゲートは何も適用しない
pass② バランスオラクル(\(f(x)=x_1 \oplus x_2 \oplus x_3 \oplus x_4\))の実装
バランス関数は、入力の半分で出力が \(0\)、残りの半分で出力が \(1\) となる関数です。
今回は、最もシンプルなバランス関数の一つである「全ての入力ビットのXOR(排他的論理和)」を採用します。
\(f(x_1 x_2 x_3 x_4) = x_1 \oplus x_2 \oplus x_3 \oplus x_4\)
上記の関数は、入力 \(x_1 \sim x_4\) の中で \(1\) の数が奇数であれば出力 \(1\) を、偶数であれば出力 \(0\) を返します。
②-1. XOR論理とCNOTゲート
量子回路において、XOR操作はCNOT(制御NOT)ゲートで表現されましたよね。
忘れてしまった方は以前の記事で再確認しておきましょう。
今回の \(f(x)\) は、\(x_1 \oplus x_2 \oplus x_3 \oplus x_4\) の結果を \(q[4]\) に作用させる操作に相当します。
これは、それぞれの入力ビット \(x_i\) を制御ビットとする \(\mathbf{CNOT}\) ゲートを、出力量子ビット \(q[4]\) に順次適用することで、シンプルかつ確実に実現できます。
\(U_f (|x\rangle |q_4\rangle) = |x\rangle |q_4 \oplus (x_1 \oplus x_2 \oplus x_3 \oplus x_4)\rangle\)
②-2. Qiskitコードによる実装
この方針に基づき、入力 \(q[0] \sim q[3]\) のそれぞれを制御ビットとするCNOTを出力 \(q[4]\) に適用する、簡潔なループ構造を採用します。
# === 2. オラクル定義関数 B: バランス関数 (XOR) ===
def oracle_balance_xor(qc, input_qubits, output_qubit):
"""
バランス関数 f(x)=x1 ⊕ x2 ⊕ x3 ⊕ x4 を実装するオラクル。
各入力ビットを制御ビットとするCNOTを出力ビットに順次適用することで、XORを実現する。
"""
for q in input_qubits:
qc.cx(q, output_qubit)第4章:Qiskitプログラム全文と実行準備
これまでに構築した共通回路の骨子と、定数/バランスの2つのオラクルを結合し、完全な実行プログラムを作成します。
実行の前に、次のライブラリがインストールされていることを確認してください。
# 必要なライブラリ
# pip install qiskit qiskit-aer① Qiskitプログラム全文
以下に示すプログラムは、定数関数(\(f(x)=0\))の判定と、バランス関数(\(f(x)=x_1 \oplus \dots\))の判定を連続して実行できる構成になっています。
コード全体をコピー&ペーストし、VS Codeで実行することができます。
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit_aer import AerSimulator # シミュレーターを使用
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt
# --- 1. オラクル定義関数 A: 定数関数 f(x)=0 ---
def oracle_constant_zero(qc, input_qubits, output_qubit):
""" 定数関数 f(x)=0 を実装するオラクル。恒等操作(何もしない)。 """
pass
# --- 2. オラクル定義関数 B: バランス関数 (XOR) ---
def oracle_balance_xor(qc, input_qubits, output_qubit):
"""
バランス関数 f(x)=x1 ⊕ x2 ⊕ x3 ⊕ x4 を実装するオラクル。
各入力ビットを制御ビットとするCNOTを出力ビットに順次適用することで、XORを実現する。
"""
for q in input_qubits:
qc.cx(q, output_qubit)
# --- 3. ドイッチュ・ジョサ回路の共通構造を構築する関数 ---
def create_deutsch_jozsa_circuit(num_qubits, oracle_func):
"""
n=4の場合、num_qubitsは4。合計5量子ビットを使用する。
オラクル関数を引数として受け取り、回路を構築する。
"""
qr = QuantumRegister(num_qubits + 1, name='q')
cr = ClassicalRegister(num_qubits, name='c')
qc = QuantumCircuit(qr, cr)
input_qubits = qr[:num_qubits]
output_qubit = qr[num_qubits]
# Step 1: 出力ビットの準備 (|-\rangle 状態)
qc.x(output_qubit)
qc.h(output_qubit)
# Step 2: 入力ビットの重ね合わせ
qc.h(input_qubits)
qc.barrier()
# Step 3: オラクル Uf の適用 (★引数で受け取った関数を実行)
oracle_func(qc, input_qubits, output_qubit)
qc.barrier()
# Step 4: 最終干渉 (再重ね合わせ)
qc.h(input_qubits)
qc.barrier()
# Step 5: 測定
qc.measure(input_qubits, cr)
return qc
# --- 4. 実行と結果の表示 ---
if __name__ == '__main__':
NUM_QUBITS = 4 # n=4
NUM_SHOTS = 1024 # 実行回数
sim = AerSimulator() # Qiskit Aerの高性能シミュレーターを使用
# === [A] 定数関数 f(x)=0 の実行 ===
print("--- [A] 定数関数 f(x)=0 の判定開始 ---")
qc_constant = create_deutsch_jozsa_circuit(NUM_QUBITS, oracle_constant_zero)
# 回路の実行
job_constant = sim.run(qc_constant, shots=NUM_SHOTS)
result_constant = job_constant.result()
counts_constant = result_constant.get_counts()
print(f"結果: {counts_constant}")
# グラフ描画(記事には最終的なグラフを掲載)
plot_histogram(counts_constant, title='Constant Function Result')
# === [B] バランス関数 (XOR) の実行 ===
print("\n--- [B] バランス関数 (XOR) の判定開始 ---")
qc_balance = create_deutsch_jozsa_circuit(NUM_QUBITS, oracle_balance_xor)
# 回路の実行
job_balance = sim.run(qc_balance, shots=NUM_SHOTS)
result_balance = job_balance.result()
counts_balance = result_balance.get_counts()
print(f"結果: {counts_balance}")
# グラフ描画
plot_histogram(counts_balance, title='Balanced Function Result')
plt.show()第5章:実行結果の検証
前章のコードを実行すると、定数オラクルとバランスオラクルの二つの結果が統合された一つのヒストグラムとして表示されます。
この二つの結果を比較することが、ドイッチュ・ジョサの量子優位性を明確に示します。
① 統合ヒストグラムによる結果の検証
以下が、定数関数(\(f(x)=0\))とバランス関数(\(f(x)=x_1 \oplus \dots\))の実行結果を統合したヒストグラムです。
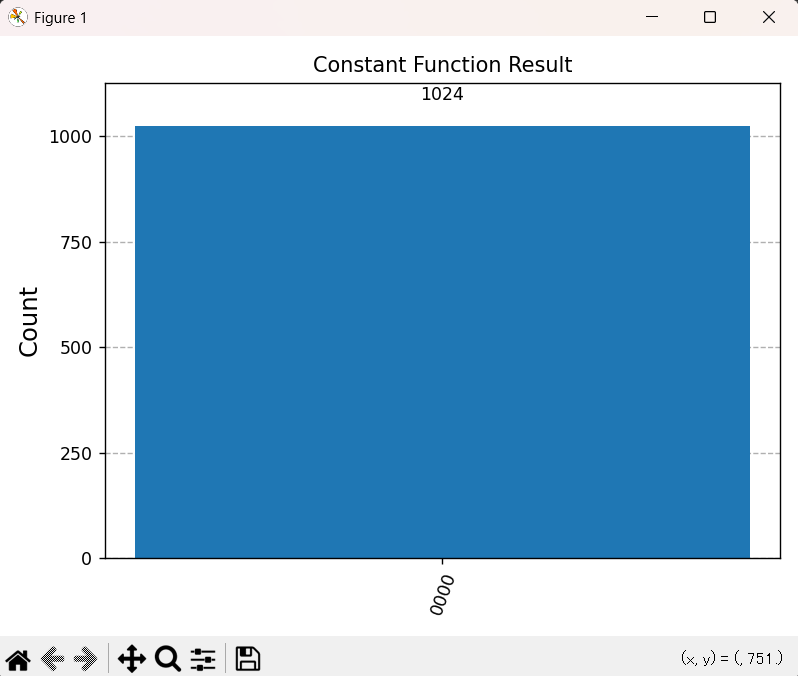
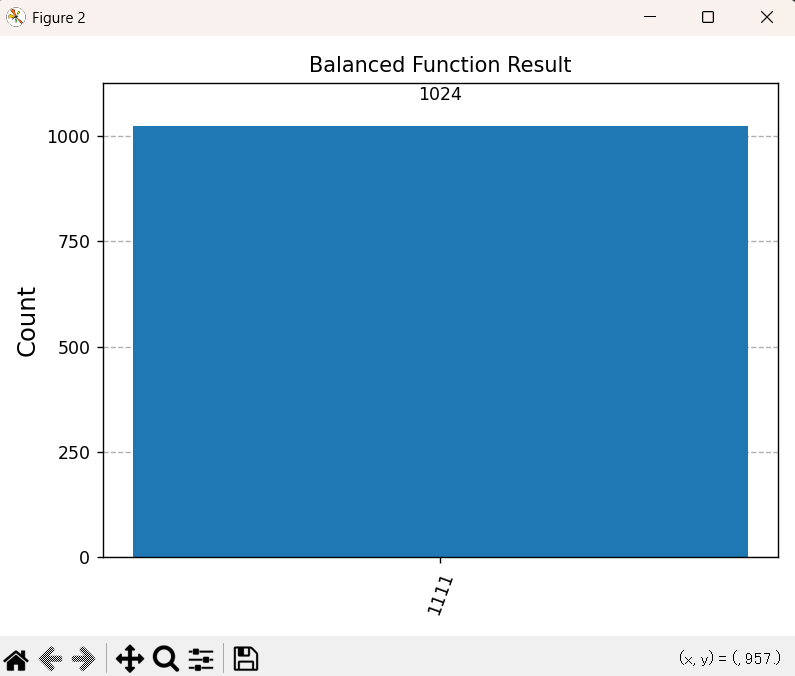
この図を分析することで、以下の決定的事実が導かれます。
| 実行された回路 | 観測結果 | 判定される関数タイプ |
|---|---|---|
| 定数オラクル | \(\boldsymbol{0000}\) に \(\boldsymbol{100\%}\) 集中 | 定数関数 |
| バランスオラクル | \(\boldsymbol{1111}\) に \(\boldsymbol{100\%}\) 集中 | バランス関数 |
② 量子判定の仕組み
この判定は、次の原則に基づいています。
- 定数関数の場合:入力ビット(\(q[0] \sim q[3]\))にHゲートとオラクルを適用した後、全ての量子ビットの位相情報が打ち消し合い、最終的な測定確率が \(\boldsymbol{|0000\rangle}\) の状態に集中します。
- バランス関数の場合:入力ビットの半数(\(2^{n-1}\) 個)の位相が反転します。この位相情報がHゲート(Step 4)によって測定確率に変換され、\(\boldsymbol{|0000\rangle}\) 以外の特定の状態(今回採用したXORオラクルでは \(\boldsymbol{|1111\rangle}\))に集中します。
【結果の解釈(最終判定基準)】
- \(\boldsymbol{0000}\) が観測された \(\Rightarrow\) 定数関数である。
- \(\boldsymbol{0000}\) 以外の状態が観測された \(\Rightarrow\) バランス関数である。
たった1回のオラクル操作で、定数関数とバランス関数の明確な判定に成功したことが、ドイッチュ・ジョサの最大の成果です。
③ 古典アルゴリズムとの比較(量子優位性の証明)
ここまでの結果は、第2章で設定した古典的な難題と対比することで、量子優位性(Quantum Advantage)を明確に証明します。
③-1. \(n=4\) の関数判定に必要なクエリ回数の比較
デモで設定した \(n=4\) のケースでは、\(2^4=16\) 通りの入力パターンがありました。
この場合、古典コンピューターと量子コンピューターが、関数タイプを確定させるために必要な最悪ケースのクエリ回数は以下の通りです。
| 判定方法 | 判定に必要なオラクルクエリ回数 |
|---|---|
| 古典的アプローチ | \(2^{n-1} + 1 = 2^3 + 1 = \mathbf{9 \text{ 回}}\) |
| ドイッチュ・ジョサ | \(\mathbf{1 \text{ 回}}\) |
③-2. 指数関数的な優位性(スケールメリット)
この優位性は、\(n\) が大きくなるにつれて劇的に拡大します。
- 古典コンピューター: \(O(2^n)\) に比例する回数が必要(指数関数的)。
- 量子コンピューター: 常に \(\boldsymbol{O(1)}\) で一定。
\(n=30\) の関数を判定する場合、古典コンピューターは \(2^{29}\) 回、すなわち約5億回の問い合わせが必要になる計算ですが、ドイッチュ・ジョサはわずか1回で判定を完了します。
ドイッチュ・ジョサのアルゴリズムは、特定の情報処理タスクにおいて、量子コンピューターが古典コンピューターに対して指数関数的な高速化を実現できるという、量子計算の可能性を世界で初めて明確に示したのです。
まとめ
本記事では、ドイッチュ・ジョサのアルゴリズムを「量子重ね合わせ」と「量子干渉」という二つの主要な武器を使って構築し、その圧倒的な効率性を確認しました。
- 重ね合わせ(Step 2): 全ての入力パターン(\(2^n\) 通り)を同時にオラクルに投げ込むことで、古典コンピューターの試行回数の課題を回避しました。
- 量子干渉(Step 4): 最終的なHゲートが、オラクルを通じて得られた位相情報を\(\boldsymbol{0000}\)または\(\boldsymbol{1111}\)のどちらかに集約させることで、たった1回で判定を完了させました。
ドイッチュ・ジョサのアルゴリズムは、特定の情報処理タスクにおいて、量子コンピューターが古典コンピューターに対して指数関数的な高速化を実現できるという、量子計算の可能性を世界で初めて明確に示したのです。
今日のショアのアルゴリズムやグローバーのアルゴリズムといった、より実用的な量子アルゴリズムの誕生に繋がる、量子計算史における金字塔と言って過言ではないでしょう。



コメント