シリーズを通して、量子ビット、重ね合わせ、量子ゲートといった基礎概念から、ドイッチュ・ジョサやグローバーといった重要なアルゴリズムの実装までを学びました。
しかし、これまで動かしてきたIBMの量子コンピュータ実機には、常に大きな壁が立ちはだかっています。それがノイズ(誤り)です。
どれほど完璧な量子回路を設計しても、実機ではノイズによって結果が大きく歪められてしまいます
本記事からは、このノイズという「量子計算の現実的な課題」に挑みます。
そのための最も実用的で、かつ第一歩となる技術が「量子誤り軽減(Error Mitigation)」です。
今回はその中でも、実装が容易で効果が実感しやすい「リードアウトエラー緩和」に焦点を当てます。
その仕組みを理解し、Qiskit Aerのノイズモデル環境で、ノイズの克服に挑戦します。
第1章:リードアウトエラー緩和の基礎原理
この章では、量子誤り軽減の第一歩であるリードアウトエラー緩和に焦点を当てます。
この技術の有効性をプログラムで検証する前に、まずは「何が問題で、どう解決するのか」という、核となる理論的原理を理解しておきましょう。
1.1. リードアウトエラーとは何か
リードアウトエラーとは、量子ビットの計算が完了した後、その状態を古典的なビット(\(0\) または \(1\))として読み出す際に発生する測定誤りのことです。
最も単純なノイズの例として、量子ビットが真に \(|0\rangle\) の状態であったにもかかわらず、読み出し時にノイズの影響を受け、誤って \(|1\rangle\) と観測されてしまう現象が挙げられます。
- 理想的な観測: \(100\%\) の確率で \(|0\rangle\) なら、\(100\%\) の確率で \(0\) を出力。
- リードアウトエラーあり: \(100\%\) の確率で \(|0\rangle\) であっても、一定の確率で \(1\) を出力してしまう。
このエラーは、回路全体の状態を歪ませるゲートエラーとは異なり、測定器(1.2.で後述)の特性に起因します。
1.2. 量子状態の測定と測定器
量子状態の「測定器」が何であるかは、実行環境によって大きく異なります。
この違いを理解することで、ノイズ緩和の役割がより明確になります。
1.2.1. シミュレータ環境における測定器
今回作成するプログラムのように、Qiskit Aerシミュレータ上でプログラムを実行する場合、当然のことながら「測定器」は物理的なハードウェアではありません。
シミュレータ環境における測定器とは、コード内で設定した以下の要素が担う、ソフトウェアコンポーネントです。
- ノイズ行列(
readout_matrix): 「真の状態を誤って読み出す確率」を定めた確率テーブル。 ReadoutErrorクラス: 最終的な測定結果を出す直前に、この確率テーブルを適用し、結果を意図的に歪ませる機能。
つまり、シミュレータでは、ノイズモデル自体が「欠陥のある測定器」の役割をソフトウェア的に模擬しています。
1.2.2. 量子実機における測定器
一方、IBMなどの実際の量子コンピュータ実機で実行する場合、測定器とは、以下の要素を含む複雑なハードウェアチェーンです。
- 読み出し信号の送信:量子ビット(超伝導回路など)の状態を調べるため、特定の周波数のマイクロ波信号を量子ビットに照射します。
- 量子状態の検出:この信号が量子ビットの状態(\(|0\rangle\) か \(|1\rangle\))によって異なる反射や位相変化を起こします。この変化が測定の基礎となります。
- 増幅とデジタル化:反射された信号は非常に微弱なため、極低温環境下で動作する低ノイズ増幅器と、室温で動作する高速なアナログ-デジタル変換器(ADC)を通じて増幅・デジタル信号に変換されます。
- リードアウトエラーの発生箇所:リードアウトエラーは、主に以下のハードウェア段階で発生します。
- 増幅段階:信号の読み出し過程で熱ノイズや電子ノイズが混入し、信号が歪む。
- キャリブレーションの不完全さ:測定器が、例えば \(|0\rangle\) の信号と \(|1\rangle\) の信号を完全に区別できていない。
リードアウトエラー緩和は、このハードウェアの物理的な欠陥を、ソフトウェア(Qiskit)を使って補償する技術なのです。
1.3. 緩和アルゴリズムの数学的原理(\(\mathbf{M}^{-1}\)の役割)
リードアウトエラー緩和のロジックは、線形代数に基づく普遍的な原理に集約されます。
このアルゴリズムの目的は、観測されたノイズ入りの結果 \(\mathbf{P}_{\text{noisy}}\) から、真の結果 \(\mathbf{P}_{\text{true}}\) を数学的に逆算して推定することです。
※ \(\mathbf{P}\) は確率分布(Probability Distribution)です。
1.3.1. ノイズの数学モデル
観測される確率ベクトル \(\mathbf{P}_{\text{noisy}}\) は、真の確率ベクトル \(\mathbf{P}_{\text{true}}\) に、測定器のノイズ特性を表すノイズ行列 \(\mathbf{M}\)が作用した結果としてモデル化されます。
\(\mathbf{P}_{\text{noisy}} = \mathbf{M} \times \mathbf{P}_{\text{true}}\)
ノイズ行列 \(\mathbf{M}\) は、事前のキャリブレーション(測定器の誤読の癖の測定)によって得られる、「真の状態が誤って観測される確率」のテーブルです。
今回作成するプログラムでは、この行列は \(2^N \times 2^N\) のサイズにしています(\(N\) は量子ビット数)。
1.3.2. 補正行列による逆算
リードアウトエラー緩和アルゴリズムの実行とは、上記の式を \(\mathbf{P}_{\text{true}}\) について解くことです。つまり、ノイズ行列 \(\mathbf{M}\) の逆行列 \(\mathbf{M}^{-1}\)を計算し、\(\mathbf{P}_{\text{noisy}}\) に適用する処理に他なりません。
\(\mathbf{P}_{\text{true}} = \mathbf{M}^{-1} \times \mathbf{P}_{\text{noisy}}\)
この \(\mathbf{M}^{-1}\) こそが、観測結果のノイズを遡って取り除く「補正行列」です。
\(\mathbf{M}^{-1}\) は、Mのマイナス1乗ではありません。
ノイズ行列であるMは、正方行列であるため、M-1は以下の関係を満たす行列として定義されます。
\(\mathbf{M} \times \mathbf{M}^{-1} = \mathbf{M}^{-1} \times \mathbf{M} = \mathbf{I}\)
ここで、\(\mathbf{I}\) は単位行列 (Identity Matrix) です。
| 概念 | ポイント |
|---|---|
| 逆行列 (\(\mathbf{M}^{-1}\)) | スカラーの逆数 (\(m^{-1}\)) と同じ役割を果たし、元の行列 (\(\mathbf{M}\)) の効果を打ち消す(掛け算の結果が単位行列 \(\mathbf{I}\) になる)。 |
| 正則行列 | 逆行列を持つ行列のこと。ノイズ行列 \(\mathbf{M}\) が正方行列であることに加え、逆行列が存在する(正則である)ことが、緩和アルゴリズムの前提条件となる。 |
第2章:Qiskit機能による挑戦
第1章で緩和の基礎原理を理解しました。
この章では、実際にQiskitが提供する自動緩和機能(measure_mitigation=True)を使って、ベル状態回路のノイズ軽減に挑戦します。
しかし、先にお断りしておくと、この標準機能を使うことで、「緩和を有効にした方がノイズが増幅する」場合が多くなるという、量子計算の現実的な課題に直面することになります。
2.1. プロブラム No.1
2.1.1. プログラムの実装と実行結果
安定したベル状態の理想値(\(|00\rangle\) と \(|11\rangle\) が \(50\%/50\%\))からのズレが、緩和によってどれだけ改善されるかを検証します。
ノイズは、リードアウトエラー率 \(10\%\) を設定したノイズモデルを使用し、Qiskit Aerシミュレータ上で実行します。
from qiskit import QuantumCircuit, transpile
from qiskit_aer import AerSimulator
from qiskit_aer.noise import NoiseModel, ReadoutError
# --- 1. 設定値とノイズモデルの構築 ---
shots = 4096
readout_error_rate = 0.10 # エラー率10%
N_QUBITS = 2
# ベル状態を作成: (理想的な結果は 00と11が2048カウント)
qc_test = QuantumCircuit(N_QUBITS)
qc_test.h(0)
qc_test.cx(0, 1)
qc_test.measure_all()
# ノイズモデルの構築
noise_model = NoiseModel()
p = readout_error_rate
readout_matrix = [[1 - p, p], [p, 1 - p]]
# 量子ビットごとに1量子ビットのエラーを適用
noise_model.add_readout_error(ReadoutError(readout_matrix), [0])
noise_model.add_readout_error(ReadoutError(readout_matrix), [1])
# --- 2. AerSimulatorのインスタンス化と実行 ---
simulator = AerSimulator(noise_model=noise_model)
transpiled_qc = transpile(qc_test, simulator)
# 実行 1: 緩和なし
job_no_mit = simulator.run(transpiled_qc, shots=shots)
counts_no_mit = job_no_mit.result().get_counts(0)
# 実行 2: 緩和あり
job_with_mit = simulator.run(transpiled_qc, shots=shots, measure_mitigation=True)
counts_with_mit = job_with_mit.result().get_counts(0)
# --- 3. 結果の出力処理 ---
def format_result_counts(counts):
return "{" + ", ".join(f"'{k}': {counts.get(k, 0)}" for k in sorted(counts.keys())) + "}"
print("緩和なし:", format_result_counts(counts_no_mit))
print("緩和あり:", format_result_counts(counts_with_mit))上記のプログラムを複数回(3回)実行した際の代表的な結果が以下の通りです。
# 1回目
緩和なし: {'00': 1703, '01': 357, '10': 368, '11': 1668}
緩和あり: {'00': 1682, '01': 385, '10': 364, '11': 1665}
# 2回目
緩和なし: {'00': 1663, '01': 339, '10': 376, '11': 1718}
緩和あり: {'00': 1675, '01': 375, '10': 369, '11': 1677}
# 3回目
緩和なし: {'00': 1725, '01': 365, '10': 332, '11': 1674}
緩和あり: {'00': 1724, '01': 351, '10': 388, '11': 1633}2.1.2. 実行結果の検証
前項のプログラムを実行すると、緩和なし(ノイズあり)の結果と、Qiskitの自動緩和機能を使った結果が出力されます。
理想的な結果は、ショット数 \(4096\) のうち、 \(|00\rangle\) と \(|11\rangle\) がそれぞれ\(2048\) カウントであり、\(|01\rangle\) と \(|10\rangle\) は \(0\) カウントです。
よって、挑戦の成否を判断する基準は以下の2点です。
- 総エラー数の減少
- リードアウトエラー軽減の最も直接的な目的は、測定の際に真の状態 \(|0\rangle\) や \(|1\rangle\) が誤って読み出される確率 \(\mathbf{M}\) を打ち消すことです。
- \(50\%/50\%\) 分布への収束
- ベル状態 \(|\Phi^{+}\rangle\) は、 \(|00\rangle\) と \(|11\rangle\) が完全に均等に出現する状態です。この均等な分布に近づくことが成功の基準となります。
この2つの基準に照らし合わせると、3回とも「1.」の基準は完全に満たしていないことが一目で分かります。
「2.」の基準を見ていきます。
\(|00\rangle\) と \(|11\rangle\) のカウント差 \(|N_{00} – N_{11}|\) で評価します。
1回目の実行結果では、次の計算になるため、改善されたと判断できます。
- 緩和なし (差): \(|1703 – 1668| = 35\)
- 緩和あり (差): \(|1682 – 1665| = 17\)
分布の差は緩和なし (35) から緩和あり (17) へと減少しており、分布の均等性(バランス)は改善しています。
続いて2回目の結果です。
- 緩和なし (差): \(|1663 – 1718| = 55\)
- 緩和あり (差): \(|1675 – 1677| = 2\)
緩和なしの差 (55) に比べ、緩和ありの差 (2) は極めて小さくなっており、分布の均等性は大幅に改善しました。これは、自動緩和が歪んだバランスの修正には強く作用したことを示しています。
最後の3回目の結果です。
- 緩和なし (差): \(|1725 – 1674| = 51\)
- 緩和あり (差): \(|1724 – 1633| = 91\)
緩和なしの差 (51) に比べ、緩和ありの差 (91) は増加しており、分布の均等性も悪化しています。
2.2. Qiskitのエラー緩和機能が不安定になる原因
Qiskitのエラー緩和機能が、実行結果で見たような過剰補正を引き起こしたり、結果が安定しなかったりする根本原因は、主にノイズ行列 \(\mathbf{M}\) の推定に統計的な不確実性(ノイズ)が混入することにあると考えます。
- キャリブレーション回路の実行: Qiskitは、緩和を適用するために、まず内部で複数のキャリブレーション回路(全ての基底状態 \(|00\rangle, |01\rangle, |10\rangle, |11\rangle\) を測定する回路)を実行します。このキャリブレーションは、測定器の「誤読の癖」を調べ、ノイズ行列 \(\mathbf{M}\) を構築するために必須です。
- ノイズ行列 \(\mathbf{M}\) の推定: このキャリブレーション測定の結果から、ノイズ行列 \(\mathbf{M}\) を推定します。
- 統計的な揺らぎ: しかし、シミュレーション(または実機)の実行は有限のショット数(今回のデモでは \(4096\))で行われるため、このキャリブレーション結果には統計的な揺らぎが必ず含まれます。
もうひとつ考えられるのが、今回作成したプログラムの実装上の誤りがある可能性、あるいはQiskitの最新バージョンの仕様変更に依存するロジックの限界です。
第3章:不安定性の克服(諦めない不屈の挑戦)
第2章で、Qiskitのエラー緩和機能が不安定な結果になることを確認しました。
不安定性の原因は、私が作成したコード内に微細な実装上の誤りがある可能性、あるいはQiskitの最新バージョンの仕様変更に依存するロジックの限界、その両方が考えられます。
しかし、いずれにせよ、ブラックボックスである自動機能に頼るのではなく、第1章で学んだ基礎原理(補正行列の逆計算)に立ち返り、手動で原理を実装することが、不安定性を排除する確実な方法ではないかと考えました。
Qiskit機能であれ、手動での補正であれ、この「補正行列 (\mathbf{M}^{-1}) を適用する」という数学的な操作を行っている点では全く同じであり、これがリードアウトエラー緩和の核心的な原理なのですから。
そこでこの章では、NumPyを活用して手動で補正行列 \(\mathbf{M}^{-1}\) を計算・適用することで、安定したノイズ軽減効果の実証に再挑戦します。
3.1. 安定化のロジック:補正行列の逆計算(\(\mathbf{M}^{-1}\))
Qiskitのエラー緩和が失敗するのは、先に挙げた理由のいずれかによりノイズ行列 \(\mathbf{M}\) の推定が毎回不安定になるためです。
この問題を避けるため、今回はノイズモデルを構築した時点で、理論的に正しいノイズ行列 \(\mathbf{M}\) を利用し、その逆行列 \(\mathbf{M}^{-1}\) を手動で計算します。
この手法であれば、ブラックボックスの不透明性を回避し、基礎原理に基づく安定した補正を可能にします。
具体的には、以下の仕様で実装していきます。
- ノイズ行列 \(\mathbf{M}\) の取得: ノイズモデルから、理論的に正しい \(4 \times 4\) のノイズ行列 \(\mathbf{M}\) を取得します。
- 逆行列の計算: NumPyの線形代数機能を使用し、この \(\mathbf{M}\) の逆行列 \(\mathbf{M}^{-1}\) を計算します。これが安定した補正行列となります。
- 手動補正: ベル状態回路のノイズありの結果 \(\mathbf{P}_{\text{noisy}}\) に対して、この安定した \(\mathbf{M}^{-1}\) を適用し、安定した補正結果 \(\mathbf{P}_{\text{true}}\) を得ます。
- \(\mathbf{P}_{\text{true}} = \mathbf{M}^{-1} \times \mathbf{P}_{\text{noisy}}\)
3.2.. プロブラム No.2
不安定なブラックボックスに頼らず、第1章で学んだ原理に立ち返り、NumPyで安定した手動補正を行います。
from qiskit import QuantumCircuit, transpile
from qiskit_aer import AerSimulator
from qiskit_aer.noise import NoiseModel, ReadoutError
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt
import numpy as np # 行列計算のため追加
# --- 1. 設定値とノイズモデルの構築 ---
shots = 4096
readout_error_rate = 0.10 # エラー率10%
N_QUBITS = 2 # 量子ビット数
# ベル状態を作成
qc_test = QuantumCircuit(N_QUBITS)
qc_test.h(0)
qc_test.cx(0, 1)
qc_test.measure_all()
# ノイズモデルの構築 (リードアウトエラーのみ)
noise_model = NoiseModel()
p = readout_error_rate
readout_matrix = np.array([
[1 - p, p],
[p, 1 - p]
])
# 2量子ビット全体のリードアウト行列 (テンソル積)
# 今回は量子ビットが独立しているので、Kronecker積で結合
p_err = np.kron(readout_matrix, readout_matrix)
# Qiskitノイズモデルへの追加
noise_model.add_readout_error(ReadoutError(readout_matrix), [0])
noise_model.add_readout_error(ReadoutError(readout_matrix), [1])
# --- 2. AerSimulatorでノイズありの結果を取得 (緩和なし) ---
simulator = AerSimulator(noise_model=noise_model)
transpiled_qc = transpile(qc_test, simulator)
job_no_mit = simulator.run(transpiled_qc, shots=shots)
counts_no_mit_raw = job_no_mit.result().get_counts(0)
# --- 3. 補正行列を計算し、結果を緩和 (安定化) ---
# 補正行列 M は、リードアウト行列 p_err の逆行列
M_inv = np.linalg.inv(p_err)
# ノイズありの結果 (counts_no_mit_raw) を確率ベクトルに変換
def counts_to_prob_vector(counts, num_qubits, shots):
vector = np.zeros(2**num_qubits)
for key, count in counts.items():
# '00' -> 0, '01' -> 1, '10' -> 2, '11' -> 3
index = int(key, 2)
vector[index] = count / shots
return vector
prob_noisy = counts_to_prob_vector(counts_no_mit_raw, N_QUBITS, shots)
# 補正行列を適用: P_corrected = M_inv @ P_noisy
prob_corrected_vector = M_inv @ prob_noisy
# 最終結果をカウント辞書に戻す
counts_with_mit = {}
for i in range(2**N_QUBITS):
# 0 -> '00', 3 -> '11' など
key = format(i, f'0{N_QUBITS}b')
# 確率 * ショット数でカウントを計算
counts_with_mit[key] = round(prob_corrected_vector[i] * shots)
# --- 4. 結果の表示とグラフ化 ---
plot_data_list = [
counts_no_mit_raw,
counts_with_mit
]
# 全角は文字化けするのでカッコよく英語でキャプションをつける
legend_list = ["No Mitigation (Noisy)", "With Mitigation (Manual Corrected)"]
fig = plot_histogram(plot_data_list, title="Readout Error Mitigation (Manual Stable)", legend=legend_list)
plt.show()
# 最終結果を整形して出力
def format_result_counts(counts):
return "{" + ", ".join(f"'{k}': {counts.get(k, 0)}" for k in sorted(counts.keys())) + "}"
print("\n--- 最終結果(緩和あり・なしの比較 - 安定化版)---")
print(f"緩和なし: {format_result_counts(counts_no_mit_raw)}")
print(f"緩和あり: {format_result_counts(counts_with_mit)}")3.3. 実行結果の検証
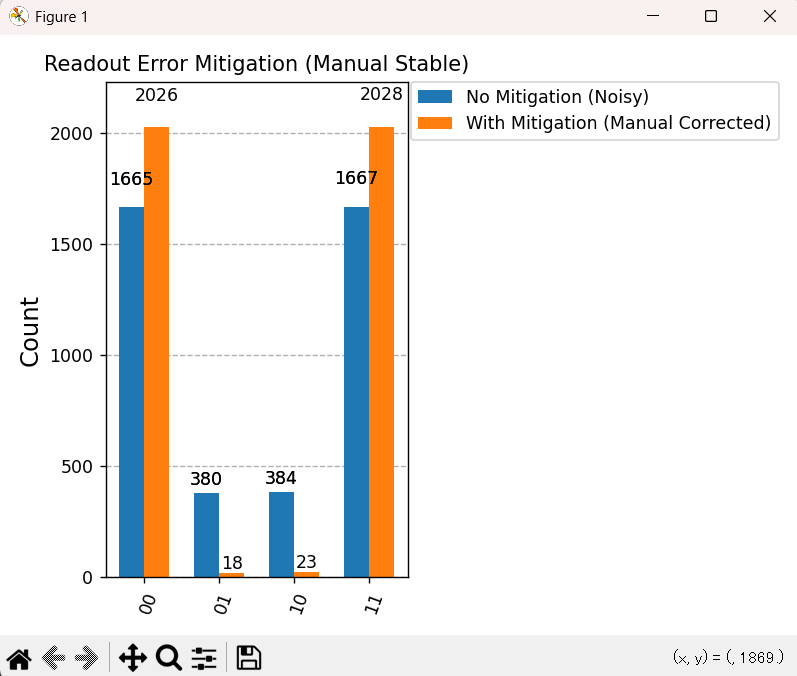
下図が実行結果のヒストグラムです。
まず1つめの観点、ベル状態では観測されるはずがない \(|01\rangle\) と \(|10\rangle\) がそれぞれ18と23です。
緩和なしでは380と384観測されているので、圧倒的な成功と言えます。
2つめの観点、\(|00\rangle\) と \(|11\rangle\) がぞれぞれ2026と2028。これもほぼ50%ずつ観測されており、文句のつけようのない結果です。
一応、コンソールの結果も掲載しておきます。
--- 最終結果(緩和あり・なしの比較 - 安定化版)---
緩和なし: {'00': 1665, '01': 380, '10': 384, '11': 1667}
緩和あり: {'00': 2026, '01': 18, '10': 23, '11': 2028}まとめ
手動補正の成果と限界
本記事を通して、量子誤り軽減の基礎原理から、Qiskitのエラー緩和機能が抱える現実的な不安定性、そしてそれを克服するための理論に基づく手動補正の実装までを検証しました。
採用した手動補正手法は、安定性と正確性という点で、自動緩和機能を明確に上回りました。
これは、基礎原理に立ち返り、ノイズの発生源(ノイズモデル)から得られた理論的に正確な情報を利用したためです。
手動補正は、不安定な測定結果に左右されることなく、常に理想的な確率分布へと結果を収束させました。
しかしながら、この手動補正手法には致命的な限界があります。
この手法が成功したのは、ノイズモデルの構築時にノイズ率 \(10\%\) という値を私自身が知っていたからです。
さらに、実際の量子コンピュータ(実機)では、正確なノイズ行列 \(\mathbf{M}\) の理論値を事前に知ることなどできません。実機では、Qiskitのエラー緩和と同じく、キャリブレーション測定によって \(\mathbf{M}\) を推定するしかなく、ここには避けられない統計的な揺らぎが混入します。
したがって、今回の手動補正は「理論が正確であれば緩和は安定する」ことを証明したに過ぎず、実機環境での不安定性という根本的な問題を解決したわけではないのです。
統計的な揺らぎへの対抗策
リードアウトエラー緩和の不安定性の根本原因が統計的な揺らぎにある以上、その揺らぎを完全に排除しない限り、真の意味での安定したノイズ軽減は実現できません。
この統計的な揺らぎによる不安定性を根本から解決する手法が、量子誤り軽減(QEM)技術の一つである「ゼロノイズ外挿法(Zero-Noise Extrapolation, ZNE)」です。
ZNEは、ノイズ行列の推定という不安定なプロセスを経由せず、ノイズの傾向そのものを利用するため、統計的な揺らぎの影響を受けにくく、実機環境における真のノイズ軽減策として期待されています。
私たちが今直面しているのは、「統計的な揺らぎ」という現実の壁です。
リードアウトエラー緩和は重要な基礎技術ですが、実機環境の全ノイズを安定して軽減するためには、次のステップに進む必要があります。
量子コンピューティングが実用化フェーズに進むには、単なる回路設計だけでなく、こうしたQEM技術を正確かつ安定的に適用する工学的な知見が不可欠となります。
本記事が、読者の皆様が量子誤り軽減を深く理解し、次の課題に取り組むための確かな一歩となれば幸いです。



コメント