量子回転ゲートを使いこなす② Ryによる状態準備とY軸回転

「量子回転ゲート三部作」の第2部へようこそ。
第1部では、\(\text{R}_Z\)ゲートが量子状態の位相（角度）をアナログに操作し、干渉制御の鍵となることを学びました。

本記事では、もう一つの主役である\(\text{R}_Y\)ゲートに焦点を当てます。
\(\text{R}_Y\)ゲートは、量子ビットの振幅（確率）を直接操作し、量子計算の出発点となる「状態準備」に不可欠なゲートです。

\(\text{R}_Z\)が「位相のズレ」を作るのに対し、\(\text{R}_Y\)は状態ベクトルを物理的に傾けることで、量子プログラミングの自由度を格段に広げます。

1 第1章：量子回転ゲート \(\text{R}_Y\) とは
2 第2章：\(\text{R}_Y\) ゲートの応用と状態準備
- 2.1 2.1. 確率を指定した状態準備の実現
- 2.2 2.2. 回転角 \(\theta\) に2を掛ける意味
3 第3章：まとめと次のステップ
- 3.1 3.1. 学習したポイントの整理
- 3.2 3.2. 量子ゲートの役割分担と次のステップ

第1章：量子回転ゲート \(\text{R}_Y\) とは

前述の通り、\(\text{R}_Y\) ゲートは、量子状態の振幅を制御する上で最も重要なゲートであり、その役割は「状態を物理的に傾ける」ことです。
この章では、\(\text{R}_Y\) ゲートの基本概念と、それが状態準備に不可欠である理由を解説します。

1.1. \(\text{R}_Y\) ゲートの役割：状態を「傾ける」

単一量子ビットの状態は、ブロッホ球 上の一点として表現されます。
第1部で扱った \(\text{R}_Z\) ゲートが\(Z\)軸（極）の周りを水平に回転させたのに対し、\(\text{R}_Y\) ゲートは\(Y\)軸（赤道上）を中心に回転させます。

1.1.1. 状態ベクトルをZ軸から傾ける

\(\text{R}_Y\) ゲートが初期状態 \(|0\rangle\)（ブロッホ球の北極）に作用すると、その状態ベクトルは\(Z\)軸から\(X\)軸や\(Y\)軸の方向へ物理的に傾けられます。

この傾きが起こると、状態は \(|0\rangle\) だけでなく\(|1\rangle\) の成分も持つようになり、結果として、状態は任意の確率を持つ重ね合わせ状態へと変化します。

\(\text{R}_Z\)：位相を変える（振幅は変えない）
\(\text{R}_Y\)：振幅を変える（状態を傾ける）

1.1.2. 状態準備への応用

量子アルゴリズムを実行する際、初期状態 \(|0\rangle\) のままでは意味がありません。
多くの場合、計算を開始する前に、すべての量子ビットを特定の確率分布を持つ初期状態に設定する必要があります。
これを状態準備（State Preparation）と呼びます。

\(\text{R}_Y\) ゲートは、その回転角度 \(\theta\) を調整することで、以下のように \(|0\rangle\) と \(|1\rangle\) の振幅比（確率比）を自在に制御できるため、状態準備のための最も基本的なツールとなります。

\(\text{R}_Y\) ゲートを初期状態 \(|0\rangle\) に作用させた場合の、代表的な角度における結果を以下に示します。

\(\theta\)	状態	測定確率
\(\theta = 0\)	\(\|0\rangle\)	\(P(0) : P(1) = 100\% : 0\%\)
\(\theta = \pi/2\)	\(\frac{1}{\sqrt{2}}(\|0\rangle + \|1\rangle)\)	\(P(0) : P(1) = 50\% : 50\%\)
\(\theta = \pi\)	\(-\|1\rangle\)	\(P(0) : P(1) = 0\% : 100\%\)

\(\theta = 0\)の場合、ブロッホ球上の位置、および測定によって得られる確率分布が、初期状態から変化なし
\(\theta = \pi/2\)の場合、\(\text{H}\)ゲートと同じ重ね合わせ状態を生成
\(\theta = \pi\)の場合、\(\text{NOT}\)（\(\text{X}\)）ゲートと同じ反転（フリップ）

1.2. \(\text{R}_Y\)ゲートのユニタリ行列と作用

1.2.1. 行列の作用

\(\text{R}_Y\) ゲートは、以下の \(2 \times 2\) ユニタリ行列で数学的に定義されます。

\(U_{\text{Ry}}(\theta) =\)

\(\begin{pmatrix} \cos(\theta/2) & -\sin(\theta/2) \\ \sin(\theta/2) & \cos(\theta/2) \end{pmatrix}\)

この行列を初期状態 \(|0\rangle\) に作用させると、状態は\(\text{Z}\)軸から\(\text{X}\)軸方向に傾き、\(\cos\)と\(\sin\)の項を持つ重ね合わせ状態が生成されます。

\(U_{\text{Ry}}(\theta) |0\rangle =\)

\(\cos(\theta/2) |0\rangle + \sin(\theta/2) |1\rangle\)

ここで、状態ベクトルにおける \(|0\rangle\) の振幅は \(\cos(\theta/2)\)、 \(|1\rangle\) の振幅は \(\sin(\theta/2)\) となり、回転角 \(\theta\) の調整によってこれらの振幅（確率）が直接制御されることが分かります。

1.2.2. \(\text{R}_Z\)との決定的な違い：実数 vs 複素数

\(\text{R}_Y\) ゲートと \(\text{R}_Z\) ゲートは、どちらも回転ゲートですが、行列を構成する成分に決定的な違いがあります。

\(\text{R}_Y\) の行列を構成する要素が実数 (\(\cos, \sin\)) のみであるのに対し、\(\text{R}_Z\) 行列の構成要素には複素数 (\(e^{\pm i\theta/2}\)) が含まれます。

それにより、生成される重ね合わせ状態にも違いが生じます。
\(\text{R}_Y\)が実数の振幅を持つ重ね合わせを生成するのに対し、\(\text{R}_Z\)は位相を持つ重ね合わせ (\(\frac{1}{\sqrt{2}}(|0\rangle \pm i|1\rangle)\) など)を生成します。

この実数成分のみで構成されるという点が、\(\text{R}_Y\) ゲートがブロッホ球の\(\text{X}\)-\(\text{Z}\)平面上で状態の方向を物理的に変化させ、振幅を直接操作する上で非常に重要になります。

1.3. Qiskitによる\(\text{R}_Y\)の実装と実行

\(\text{R}_Y\) ゲートの作用を実際に確認するため、Qiskitを使って量子回路を構築し、状態ベクトルシミュレーションを行います。

今回のプログラムでは、量子状態を数学的に表現するためのベクトルオブジェクトである Statevector を使用します。

1.3.1. ライブラリのインポートと回路の準備

まず、必要なライブラリをインポートし、1量子ビットからなる量子回路を構築します。

from qiskit import QuantumCircuit
from qiskit.quantum_info import Statevector
from qiskit.visualization import plot_bloch_multivector
import numpy as np
import matplotlib.pyplot as plt

# 1量子ビット、1古典ビットの回路を作成
qc = QuantumCircuit(1, 1)

# 初期状態は |0⟩
print(Statevector(qc).draw('text'))
# 期待される出力: [1.+0.j,0.+0.j]

実行結果

[1.+0.j,0.+0.j]

【参考】上記の実行結果 [1.+0.j,0.+0.j] は、線形代数での縦ベクトル \(\begin{pmatrix} 1 \\ 0 \end{pmatrix}\) になり、量子コンピューティングにおいては \(|0\rangle\)（基底状態）を表す標準的な形式です。

ちなみに \(j\) は、虚数 \(i\) の代わりに使われるアルファベットです。

1.3.2. \(\text{R}_Y\) ゲートの適用（\(\theta = \pi/2\)）

次に、\(\text{R}_Y(\theta)\) ゲートを量子ビット0に適用します。

ここでは、\(\theta = \pi/2\) を用います。これは、状態を \(\displaystyle\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\) へと傾ける操作です。

「1.3.1.」のコードに続けて、以下の実装を追加してください。

# R_Y(pi/2) を適用
theta = np.pi / 2
qc.ry(theta, 0)

# 適用後の状態ベクトルを確認
state = Statevector(qc)
print(state.draw('text'))

# 期待される出力: [0.70710678+0.j,0.70710678+0.j] に近い値

実行結果

[0.70710678+0.j,0.70710678+0.j]

【参考】上記の実行結果 [0.70710678+0.j,0.70710678+0.j] は、50%と50%の重ね合わせ状態を表しています。
線形代数での縦ベクトルでは \(\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 1 \end{pmatrix}\) になり、量子コンピューティングにおいては \(|+\rangle\) (プラス状態) と呼ばれる状態、または \(\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\) となります。

1.3.3. ブロッホ球での可視化

この状態をブロッホ球で確認すると、状態ベクトルが\(\text{Z}\)軸から\(\text{X}\)軸へと45度 (\(\theta/2\) ラジアン) 傾いていることが視覚的に理解できます。

作成中のプログラムの最後に、以下のコードを追加してください。

# ブロッホ球で状態を確認
plot_bloch_multivector(state)
plt.show()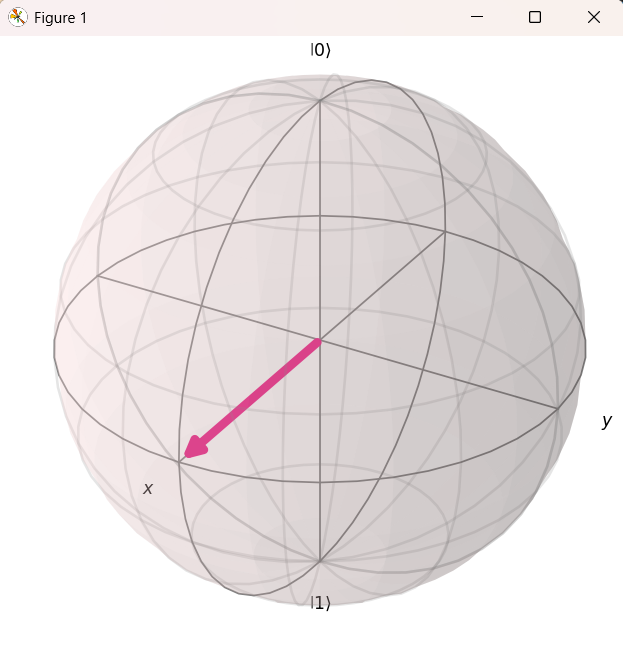

実行結果のブロッホ球

1.4. \(\text{H}\)ゲートは\(\text{R}_Y\)の特殊ケース

アダマール (\(\text{H}\)) ゲートが、\(\text{R}_Y\) ゲートをある特定の角度に設定したときと同じ働きをすることを解説します。
その角度とは、\(\pi/2\) ラジアン (\(90^\circ\)) です。

アダマール (\(\text{H}\)) ゲートは、状態 \(|0\rangle\)（てっぺん）を、真横の \(\text{X}\) 軸の位置に移動させます。これにより、50%:50%の重ね合わせ状態が作られます。

セクション1.3.で実行した\(\text{R}_Y(\pi/2)\)（90度回転）の操作も、 \(|0\rangle\) の状態を真横の \(\text{X}\) 軸に移動させました。
そうです。こちらも50%:50%の重ね合わせ状態を生成するのです。

よって、\(\text{H}\)ゲートは、\(\text{R}_Y\)ゲートの角度を「\(90\)度 (\(\pi/2\) ラジアン)」にしたときと、全く同じ働きをする特殊なケースであると理解できます。

第2章：\(\text{R}_Y\) ゲートの応用と状態準備

前章で \(\text{R}_Y\) ゲートの基本的な回転操作と、\(\text{H}\) ゲートとの特殊な関係を理解しました。
この章では、\(\text{R}_Y\) ゲートが本領を発揮する状態準備（State Preparation）の実践的な側面に焦点を当てます。
\(\text{R}_Y\) の角度 \(\theta\) を精密に制御することで、量子探索や最適化アルゴリズムで使用する特定の確率分布を持つ初期状態を、Qiskitで自在に構築できます。

2.1. 確率を指定した状態準備の実現

このセクションでは、\(\text{R}_Y\) ゲートを使って「\(\text{P}(0) = 80\%\)、\(\text{P}(1) = 20\%\)」といった、特定の確率を持つ重ね合わせ状態をどのように作成するかを解説します。

2.1.1. 必要な回転角 \(\theta\) の求め方

\(\text{R}_Y\) ゲートが初期状態 \(|0\rangle\) に作用した後の、測定確率（振幅の二乗）は、第1部記事でも紹介した以下の三角関数で与えられることを利用します。

以下は、繰り返し使用して覚えておきたい重要な数式です。

測定結果 \(|0\rangle\) となる確率 \(P(0)\): \(\cos^2(\theta/2)\)
測定結果 \(|1\rangle\) となる確率 \(P(1)\): \(\sin^2(\theta/2)\)

目標とする確率 \(\text{P}(1)\) から、必要な回転角 \(\theta\) を求める式は以下の通りです。

\(\theta = 2 \cdot \arcsin\left(\sqrt{\text{P}(1)}\right)\)

2.1.2. 実践例：\(P(1) = 20\%\) の状態準備

目標確率 \(\text{P}(1) = 0.2\) を上記公式に代入し、必要な回転角 \(\theta\) を算出します。

三角関数を逆算する必要がありますが、実際のプログラミングでは、読者が手計算する必要はありません。
Pythonの標準的な数値計算ライブラリである NumPy というツールを使えば、この複雑な計算を一発で実行できます。

この「確率から角度を逆算する機能」を、NumPy の arcsin 関数に担当させます。

目標確率の準備: \(\text{P}(1) = 0.2\)
NumPyによる計算: \(\text{theta} = 2 \times \text{np.arcsin}(\sqrt{0.2})\)
結果: \(\theta \approx 0.9273\) ラジアン

【参考】として、数学的な計算手順も記載しておきます。

\(\sqrt{0.2} \approx 0.44721\)
\(\arcsin(0.44721) \approx 0.46365\) ラジアン
\(\theta = 2 \cdot 0.46365 \approx **0.9273**\) ラジアン

2.1.3. Qiskitによる \(P(1)=20\%\) の状態準備の実装

前項で求めた角度 \(\theta \approx 0.9273\) ラジアンを実際にQiskitのコードに組み込み、シミュレーション結果（確率）が目標の \(\text{P}(1)=20\%\) になることを検証します。

2.1.3.1. 実装コードと実行

from qiskit import QuantumCircuit
from qiskit.quantum_info import Statevector
from qiskit.visualization import plot_bloch_multivector
import matplotlib.pyplot as plt
import numpy as np

# --- 1. 定数の設定 ---
# 目標とする |1> の確率 P(1) = 0.2
P1 = 0.2

# 必要な回転角度 theta の計算: theta = 2 * arcsin(sqrt(P1))
theta = 2 * np.arcsin(np.sqrt(P1))

# --- 2. 回路の構築と実行 (R_Y(theta)) ---
qc = QuantumCircuit(1)
qc.ry(theta, 0)

# 適用後の状態ベクトルを確認
state = Statevector(qc)
print(state.draw('text'))

実行結果

[0.89442719+0.j,0.4472136 +0.j]

2.1.3.2. 実行結果の状態ベクトルの確認

実行結果 [0.89442719+0.j, 0.4472136+0.j] 読み取り方と確率の検証は以下の通りです。

適用後の状態ベクトルからは、以下の振幅（確率の元となる値）が得られました。

\(|0\rangle\) の振幅 (\(\alpha\)): \(\approx 0.8944\)
\(|1\rangle\) の振幅 (\(\beta\)): \(\approx 0.4472\)

それぞれの振幅を二乗することで、測定確率が目標通りになるかどうか計算します。

\(\text{P}(0)\) の確率: \(|\alpha|^2 \approx 0.89442719^2 = 0.8000\) (80%)
\(\text{P}(1)\) の確率: \(|\beta|^2 \approx 0.44721360^2 = 0.2000\) (20%)

目標とした \(\text{P}(1)=20\%\) の確率を持つ重ね合わせ状態が、\(\text{R}_Y(\theta)\) ゲートによって生成されたことを確認できました。

2.1.3.3. ブロッホ球での可視化

前項で状態ベクトルが目標の \(80\% : 20\%\) になったことを確認しました。
この項では、この状態がブロッホ球のどこに位置しているかを可視化することで、\(\text{R}_Y\) ゲートが状態をどのように「傾けた」かを視覚的に理解します。

期待される可視化の結果は次の通りです。

\(\text{R}_Y\) ゲートは \(\text{Y}\) 軸を中心に回転するため、状態は \(\text{X}-\text{Z}\) 平面内（球の側面）に留まります。
状態ベクトルが、北極 (\(\text{P}(0)=100\%\)) から赤道方向へ緩やかに (20%分) 傾いている様子を確認します。

前項のコードに続けて、以下の可視化コードを追加してください。

# ブロッホ球で状態を確認
plot_bloch_multivector(state)
plt.show()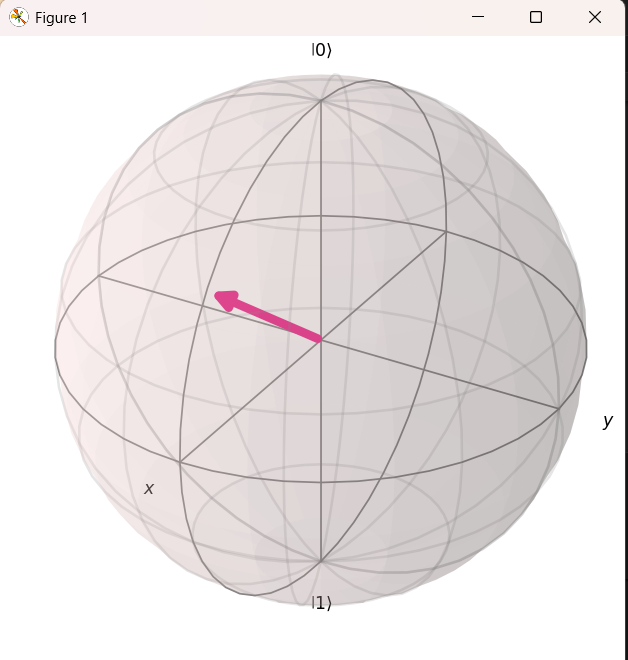

実行結果のブロッホ球

2.2. 回転角 \(\theta\) に2を掛ける意味

セクション2.1.では、目標の確率 \(\text{P}(1)\) から \(\text{R}_Y\) ゲートの回転角 \(\theta\) を算出する際に、2倍の係数（\(\times 2\)）が必要となることを確認しました。

\(\theta = 2 \cdot \arcsin\left(\sqrt{\text{P}(1)}\right)\)

実際にQiskitでプログラムする際は、以下のコードで必要な角度を算出しました。

P1 = 0.2 # 20% の場合
theta = 2 * np.arcsin(np.sqrt(P1))

これは、\(\text{R}_Y\) ゲートの引数が、ブロッホ球上で状態ベクトルが実際に動く角度とは異なり、その2倍の角度を要求するという特殊な仕様になっているためです。

結論として、\(\text{R}_Y\) ゲートを使って目標確率を設定する場合、この \(\times 2\) の操作がなければ、プログラムは意図した確率とは異なる結果を返すことになります。
状態準備を正確に行うための注意点として、この \(\times 2\) の計算を必ず行ってください。

第3章：まとめと次のステップ

3.1. 学習したポイントの整理

本記事「量子回転ゲート三部作・第2部」では、\(\text{R}_Y\) ゲートに焦点を当て、以下の重要なスキルを習得しました。

\(\text{R}_Y\) ゲートの役割: 状態の振幅（確率）を制御すること。
状態準備の実践: 任意の測定確率 \(\text{P}(1)\) から、\(\text{R}_Y\) ゲートの引数 \(\theta\) を計算する方法。
- \(\theta = 2 \cdot \arcsin\left(\sqrt{\text{P}(1)}\right)\)
\(\text{R}_Y\) の引数に関する注意点: ブロッホ球上の回転角の2倍を引数に与える必要があること。