量子コンピューティングにおいて基本的かつ重要な操作、量子回転ゲート。
前回までの回転ゲート三部作では、第1部で「位相の制御」(\(\text{R}_Z\)) を、第2部で「振幅の制御」(\(\text{R}_Y\)) を、そして前回の記事で「X軸周りの回転」(\(\text{R}_X\)) を学習しました。
これら三つの回転ゲートは、ブロッホ球上の三次元の回転軸として単一量子ビットを意図通りに操作することを可能にします。
本記事では、これまでの知識を統合し、単一量子ビット操作の究極の汎用ゲートである\(\mathbf{U}3\) ゲートを解説します。
\(\text{U}3(\theta, \phi, \lambda)\) ゲートは、三つのパラメータを持つことで、\(\text{R}_X, \text{R}_Y, \text{R}_Z\) のすべての操作を一つに集約し、ブロッホ球上の任意の点へ量子状態を到達させることを可能にします。
本記事を通して、\(\text{U}3\) ゲートの操作方法、その抽象的な意味、そして実際の実装と検証を習得し、単一量子ビット操作の理論的および実践的な最終理解を確立しましょう。
目次
第1章:\(\mathbf{U}3\) ゲートの導入と汎用性の証明
本章では、\(\mathbf{U}3\) ゲートの持つ三つのパラメータ (\(\theta, \phi, \lambda\)) が、どのようにブロッホ球上の三次元的な操作の自由度を完全に表現しているのかを定義します。
その上で、\(\mathbf{U}3\) ゲートが、これまでの基本的な回転ゲートをいかに簡単に置き換えられるかを理解し、単一量子ビット操作の完全性(Completeness)を確立します。
1.1. \(\mathbf{U}3\) ゲートの役割と定義
1.1.1. \(\mathbf{U}3\) ゲートの役割:単一量子ビット操作の究極形
\(\mathbf{U}3\) ゲートは、Qiskitで提供される最も包括的な単一量子ビットゲートです。
これまでに学んだ全ての基本的な回転ゲート(\(\text{R}_X, \text{R}_Y, \text{R}_Z\))は、ブロッホ球上の特定の軸周りの回転しか行えませんでしたが、\(\mathbf{U}3\) ゲートは一つの命令で、ブロッホ球上の任意の点に量子状態を移動させる能力を持っています。
- 役割: \(\mathbf{U}3\) ゲートは、単一量子ビットに適用可能な全ての操作を一つに統合したものです。
- 汎用性: 量子回路において、\(\mathbf{U}3\) ゲートは全ての単一量子ビットゲートを置き換えることが可能な汎用ゲートとしての機能を持っています。
1.1.2. \(\mathbf{U}3\) ゲートの定義とパラメータ
\(\mathbf{U}3\) ゲートは、三つの独立したパラメータ(角度)を使って、「\(\mathbf{U}3(\theta, \phi, \lambda)\)」という形式で定義されます。
Qiskitでは、量子回路オブジェクトに対して.u()メソッドとして提供されます。
| パラメータ | 役割 |
|---|---|
| シータ \(\theta\) | 主な緯度(赤道からの角度)の制御。 ブロッホ球上の\(\text{Z}\)軸からの角度(\(\text{X}\)軸や\(\text{Y}\)軸周りの回転に相当) |
| ファイ \(\phi\) | 経度(ブロッホ球のXY平面上の角度)の制御。 位相の移動、主に\(\text{Z}\)軸周りの回転(\(\text{R}_Z\))に相当 |
| ラムダ \(\lambda\) |
1.2. パラメータが決定する物理的作用
前項の表「R3ゲートのパラメータとそれぞれの役割」の内容をもう少し詳しく解説します。
1.2.1. \(\theta\) (シータ) の作用
パラメータ \(\theta\) は、量子状態を \(\text{Z}\) 軸(極)からどれだけ離すかを制御する主要な回転角度です。
- 役割: \(\text{R}_Y\) ゲートが\(\text{Y}\)軸周りの回転で状態を\(\text{Z}\)軸から遠ざけたのと同様に、\(\theta\) は状態の純粋な振幅の制御に関与します。
- 初期状態への作用: 初期状態 \(|0\rangle\) に対して、\(\theta\) を動かすことは、北極(\(|0\rangle\))から赤道、そして南極(\(|1\rangle\))への緯度の移動を可能にします。
1.2.2. \(\phi\) と \(\lambda\) (ファイとラムダ) の作用
\(\phi\) と \(\lambda\) の二つのパラメータは、\(\theta\) によって決定された緯度(\(\text{Z}\)軸からの距離)を維持したまま、\(\text{XY}\) 平面上の位相的な位置を制御します。
- 役割: この二つのパラメータは、ブロッホ球の赤道上を回転させる役割を果たします。これは\(\text{R}_Z\) ゲートの位相操作に相当します。
- 違い: 厳密には、\(\phi\) は最初の回転の経度を、\(\lambda\) は最後の回転の経度を決定します。量子計算において、これら二つの位相は干渉効果を生み出すために不可欠な要素となります。
- プログラム上の作用: ほとんどの単一量子ビット操作は、これら三つの回転操作(\(\text{Z}\)軸回転、\(\text{Y}\)軸回転、\(\text{Z}\)軸回転)の組み合わせとして実行されます。\(\text{U}3\) ゲートは、この複雑な回転順序を隠蔽し、ユーザーが最終的な目標状態をシンプルに定義することを可能にします。
1.3. \(\mathbf{U}3\) ゲートによる \(\text{R}_X, \text{R}_Y, \text{R}_Z\) ゲートの置き換え
基本的な回転ゲート(\(\text{R}_X, \text{R}_Y, \text{R}_Z\))の操作は全て、\(\mathbf{U}3(\theta, \phi, \lambda)\) の特殊なケースとして表現できます。
\(\mathbf{U}3\) ゲートを使用すれば、単純なパラメータ操作を行うだけで、従来の回転ゲートと全く同じ効果が得られます。
この知識は、より複雑な回路を簡潔に記述する際に役立ちます。
1.3.1. \(\mathbf{U}3\) ゲートによる \(\text{R}_X\) ゲートの置き換え
\(\mathbf{U}3\) ゲートを使用して、\(\text{R}_X(\theta)\) ゲートと全く同じ回転を実現することができます。
\(\text{R}_X\) ゲートは、ブロッホ球の\(\text{X}\)軸周りの回転であり、\(\mathbf{U}3\) ゲートのパラメータを適切に設定することで、この操作を再現できます。
\(\text{R}_X(\alpha)\) の回転を\(\mathbf{U}3(\theta, \phi, \lambda)\) で置き換えると、次のとおりです。
\(\text{R}_X(\alpha) = \mathbf{U}3(\alpha, -\pi/2, \pi/2)\)
- \(\theta = \alpha\): \(\text{R}_X\) ゲートの回転角度 (\(\alpha\)) を、\(\mathbf{U}3\) の主要な回転角度 (\(\theta\)) に対応させます。
- \(\phi = -\pi/2\) と \(\lambda = \pi/2\): これら二つの位相パラメータの特別な設定により、\(\mathbf{U}3\) ゲートが\(\text{X}\)軸周りの回転軸を選択するように軸を調整します。この設定は、\(\text{R}_X\) ゲートの持つ行列表現と数学的に等価であることを意味します。
1.3.2. \(\mathbf{U}3\) ゲートによる \(\text{R}_Y\) ゲートの置き換え
\(\text{R}_Y\) ゲートは、ブロッホ球の\(\text{Y}\)軸周りの回転を行います。
これは、状態の緯度、すなわち\(\text{Z}\)軸からの角度を直接制御する上で非常に重要な操作です。
\(\mathbf{U}3\) ゲートを使用することで、この\(\text{R}_Y(\alpha)\) ゲートの操作も、二つの位相パラメータをゼロに設定するだけで置き換えられます。
\(\text{R}_Y(\alpha)\) の回転を \(\mathbf{U}3(\theta, \phi, \lambda)\) で置き換えると、次のとおりです。
\(\text{R}_Y(\alpha) = \mathbf{U}3(\alpha, 0, 0)\)
- \(\theta = \alpha\): \(\text{R}_Y\) ゲートの回転角度 (\(\alpha\)) を、\(\mathbf{U}3\) の主要な回転角度 (\(\theta\)) に直接対応させます。これは、\(\mathbf{U}3\) ゲートの持つ回転分解の仕組み上、\(\text{R}_Y\) ゲートの核心的な操作が\(\theta\)パラメータに集約されているためです。
- \(\phi = 0\) と \(\lambda = 0\): これら二つの位相パラメータをゼロに設定することで、\(\mathbf{U}3\) ゲートが\(\text{Y}\)軸周りの回転以外の余分な位相操作を行わないように固定します。この設定により、\(\text{R}_Y\) ゲートと数学的に完全に等価な操作が実現します。
1.3.3. \(\mathbf{U}3\) ゲートによる \(\text{R}_Z\) ゲートの置き換え
\(\text{R}_Z\) ゲートは、ブロッホ球の\(\text{Z}\)軸周りの回転を行います。
これは、量子状態の相対位相を制御する上で不可欠な操作であり、量子アルゴリズムにおける干渉効果を生み出す鍵となります。
この操作は、\(\mathbf{U}3\) ゲートの二つの位相パラメータ (\(\theta\) と \(\phi\)) をゼロに設定し、\(\lambda\) に回転角を割り当てることで置き換えられます。
これは、前項の \(\text{R}_Y\) ゲートが \(\phi\) と \(\lambda\) をゼロに設定したのとは、異なるパラメータを固定する点に注意が必要です。
\(\text{R}_Z(\alpha)\) の回転を \(\mathbf{U}3(\theta, \phi, \lambda)\) で置き換えると、次のとおりです。
\(\text{R}_Z(\alpha) = \mathbf{U}3(0, 0, \alpha)\)
- \(\theta = 0\) と \(\phi = 0\): \(\text{R}_Y\) ゲートの置き換えとは異なり、\(\text{R}_Z\) ゲートは回転を\(\text{Z}\)軸周りの\(\text{XY}\)平面上のみに限定するため、\(\theta\) と \(\phi\) をゼロに固定します。
- \(\lambda = \alpha\): \(\text{R}_Z\) ゲートの回転角度 (\(\alpha\)) を、\(\mathbf{U}3\) の三番目の位相パラメータ (\(\lambda\)) に直接対応させます。これにより、\(\text{Z}\)軸周りの指定された角度の回転(位相シフト)を実現します。
第2章:\(\mathbf{U}3\) ゲートの実装と三次元回転の検証
本章では、\(\mathbf{U}3\) ゲートをQiskitで自走し、三つのパラメータ (\(\theta, \phi, \lambda\)) を使ってブロッホ球上の任意のターゲット座標へ量子状態を移動させる方法を習得します。
検証は以下のスタイルで行います。
- 状態ベクトルシミュレータ(測定前の回路)を通じたブロッホ球の描画
- 確率シミュレータ(測定後の回路)を通じたヒストグラムの描画
2.1. ターゲット座標の決定
\(\mathbf{U}3\) ゲートを回路に適用する際、\(\theta, \phi, \lambda\) の三つのパラメータにどのような値を与えれば、ブロッホ球上の特定のターゲット座標に到達できるかを決定する必要があります。
三つのパラメータは、目標とする量子状態を極座標系で表したときの角度と対応します。
- \(\theta\): \(\text{Z}\)軸からの角度(緯度)。\(\mathbf{U}3\) の主要な回転角度です。
- \(\phi\): \(\text{XY}\)平面上の角度(経度)。状態の位相を制御します。
- \(\lambda\): \(\text{XY}\)平面上の角度(経度)。状態の位相を制御します。
\(\mathbf{U}3\) ゲートを使うプログラミングの核心は、「ブロッホ球のどこに行きたいか」を決めたら、それに合わせて\(\theta\) と \(\phi\) の値を決定し、コードに入力することであると言えます。
2.1.1. ターゲット座標の設定(検証用プログラムの仕様)
\(\mathbf{U}3\) ゲートの汎用性を検証するため、\(\text{X}, \text{Y}, \text{Z}\) 軸上にない、三次元空間の任意の中間点をターゲットとします。
これにより、\(\text{R}_X, \text{R}_Y, \text{R}_Z\) ゲートでは一発で到達できなかった状態を \(\mathbf{U}3\) ゲート単独で達成できることを確認します。
| 項目 | 値 | 物理的作用 |
|---|---|---|
| \(\text{Z}\)軸からの角度 (\(\theta\)) | \(\pi/4\) | 北極 (\(\text{Z}\)軸) から赤道へ\(\pi/4\) (45°) 傾ける。振幅の制御に影響する。 |
| \(\text{XY}\)平面上の角度 (\(\phi\)) | \(\pi/4\) | 赤道上の\(\text{X}\)軸から\(\text{Y}\)軸へ \(\pi/4\) (45°) ずらす。位相の制御に影響する。 |
| グローバル位相 (\(\lambda\)) | \(0\) | \(0\) に固定する。\(\lambda\) は量子状態そのもの(確率)には影響しない。 |
この設定により、ターゲットとなる量子状態 \(|\psi\rangle\) は、次の二つの条件を満たす座標に位置します。
- \(\text{XY}\)平面上の\(\text{X}\)軸と\(\text{Y}\)軸の中間点(\(\phi = \pi/4\))
- \(\text{Z}\)軸から45度(\(\theta = \pi/4\))傾いた点
2.2. 測定前の回路構築とブロッホ球の描画(プログラム1)
このプログラムは、測定前の量子状態をそのまま取得し、ブロッホ球上にプロットすることで、\(U3\) ゲートによる操作が、前セクションで設定した目標座標に正確に到達していることを検証します。
2.2.1. ライブラリのインポートとパラメータの適用
測定前の状態ベクトルを取得するために、以下のライブラリを使用します。
QuantumCircuit: 量子回路の構築Aer: Qiskitのシミュレータ(statevector)のバックエンドnumpy: 円周率 \(\pi\) (np.pi) を使った正確な角度計算plot_bloch_multivector: 検証のためのブロッホ球描画ツール
# 必要なライブラリのインポート
from qiskit import QuantumCircuit
from qiskit_aer import Aer
from qiskit.visualization import plot_bloch_multivector
import matplotlib.pyplot as plt
import numpy as np
# --- 1. 目標パラメータの設定 ---
# U3(theta, phi, lambda) = U3(π/4, π/4, 0)
theta = np.pi / 4
phi = np.pi / 4
lamda = 0.0
# --- 2. 回路の初期化 ---
qc = QuantumCircuit(1) # 量子ビットを1つ用意
# --- 3. U3ゲートの適用 ---
# qc.uの第4引数は量子ビットのインデックス
qc.u(theta, phi, lamda, 0)
# 回路の表示
print(qc) ┌──────────────┐
q: ┤ U(π/4,π/4,0) ├
└──────────────┘プログラムを実行すると、回路図がテキスト出力で得られ、想定通り\(\mathbf{U}3\) ゲートが適用されたことを確認できます。
2.2.2. ブロッホ球の描画と実行結果分析
前項 2.2.1. で作成したプログラムに以下のコードを追加してください。
定義した回路を、statevector_simulator を使って実行し、結果をブロッホ球に描画します。
# シミュレータの定義
backend = Aer.get_backend('statevector_simulator')
# 回路の実行(runを使用)
# run()は非同期ジョブを返し、result()で結果を取得
job = backend.run(qc)
result = job.result()
# 状態ベクトルを取得
# decimals=3 で出力を丸め、見やすくする
outputstate = result.get_statevector(qc, decimals=3)
# ブロッホ球を描画
plot_bloch_multivector(outputstate)
plt.show()実行結果のブロッホ球を回転させながら見ると、状態ベクトルは二つの独立した条件を満たす座標に位置していることが視覚的に確認できます。
- 条件1:状態ベクトルは、\(\text{X}\)軸と\(\text{Y}\)軸の中間点(経度 45°)を指している。(\(\phi = \pi/4\) を反映している)
- 条件2:状態ベクトルは、\(\text{Z}\)軸から 45° 傾いた位置(緯度)を指している。(\(\theta = \pi/4\) を反映している)
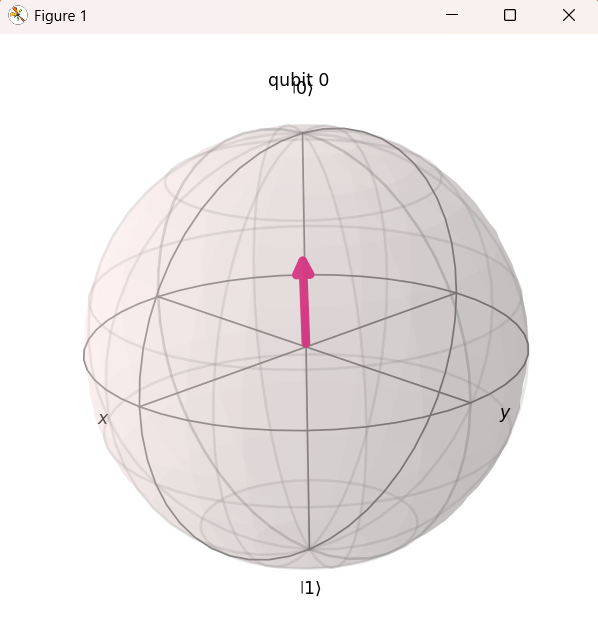
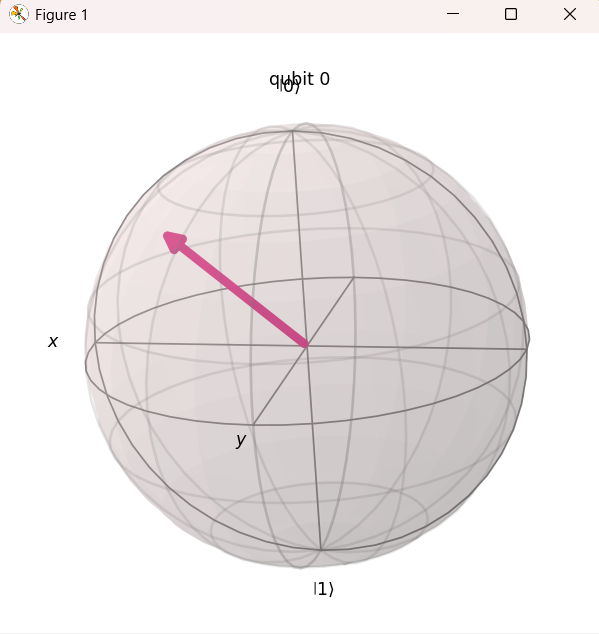
この結果から、\(\mathbf{U}3\) ゲートは、\(\text{R}_X\) や \(\text{R}_Y\) のように軸上の回転に限定されず、\(\theta\) と \(\phi\) の組み合わせによって、ブロッホ球上の任意の中間座標へ量子状態を単独操作で移動できることが確認できました。
2.3. 測定を含む回路構築とヒストグラムの描画(プログラム2)
2.3.1. 期待される確率の計算方法
プログラム2の実行により、\(\mathbf{U}3(\pi/4, \pi/4, 0)\) を適用した量子状態 \(|\psi\rangle\) を測定した際に、結果が \(|0\rangle\) または \(|1\rangle\) になる確率を予測しておきましょう。
この確率の分布(ヒストグラム)は、量子状態 \(|\psi\rangle\) の振幅(\(\theta\))から予測できます。
状態ベクトルの \(|0\rangle\) と \(|1\rangle\) の振幅は、項 2.1.1. の設定 (仕様として決めた \(\theta = \pi/4\)) により、以下の通りとなります。
- \(|0\rangle\) 状態の確率 \(P(0)\): \(\cos^2(\theta/2) = \cos^2((\pi/4)/2) = \cos^2(\pi/8)\)
- \(|1\rangle\) 状態の確率 \(P(1)\): \(\sin^2(\theta/2) = \sin^2((\pi/4)/2) = \sin^2(\pi/8)\)
\(\pi/8\) は \(22.5^\circ\) であり、\(\cos(22.5^\circ) \approx 0.9239\)、\(\sin(22.5^\circ) \approx 0.3827\) です。
したがって、期待される確率は、それぞれ以下の通りとなります。
- \(P(0) \approx 0.9239^2 \approx \mathbf{0.8535}\)
- \(P(1) \approx 0.3827^2 \approx \mathbf{0.1465}\)
この期待値の計算は、複数の公式を知っている必要がありますし、計算過程もなかなかに煩雑です。
そこで、「期待値算出プログラム」を記事最終章に巻末付録として掲載します。
角度(度数法)を入力すると、U3ゲートの測定確率P(0)とP(1)の期待値を計算する機能を持ちます。
2.3.2. Qiskitによる回路構築
以下のプログラムを、新規ファイルとして作成します。
from qiskit import QuantumCircuit
from qiskit_aer import Aer
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt
import numpy as np
# --- 1. 目標パラメータの設定 (再掲) ---
# U3(theta, phi, lambda) = U3(π/4, π/4, 0)
theta = np.pi / 4
phi = np.pi / 4
lamda = 0.0
# --- 2. 測定のための回路再構築 ---
# 量子ビット1つ (q) と古典ビット1つ (c) を用意
qc_measured = QuantumCircuit(1, 1)
# U3ゲートの適用
qc_measured.u(theta, phi, lamda, 0)
# 3. 測定操作の追加
# 量子ビット0の結果を古典ビット0に書き込む
qc_measured.measure(0, 0)
# 回路の表示
print(qc_measured) ┌──────────────┐┌─┐
q: ┤ U(π/4,π/4,0) ├┤M├
└──────────────┘└╥┘
c: 1/═════════════════╩═
0この出力結果は、\(\mathbf{U}3\) ゲート操作の後に、量子ビットが古典ビットに接続され、測定が行われていることを示しています。
2.3.3. ヒストグラムの描画と \(U3\) ゲートの検証
前項 2.3.2. で作成したプログラムに以下のコードを追加してください。
構築した測定回路(qc_measured)を、qasm_simulator で 1024 ショット実行し、結果をヒストグラムで描画する処理です。
# シミュレータの定義
backend = Aer.get_backend('qasm_simulator')
# 回路の実行(1024ショット)
job = backend.run(qc_measured, shots=1024)
result = job.result()
# 結果(カウント)を取得
counts = result.get_counts(qc_measured)
# ヒストグラムを描画
plot_histogram(counts)
plt.show()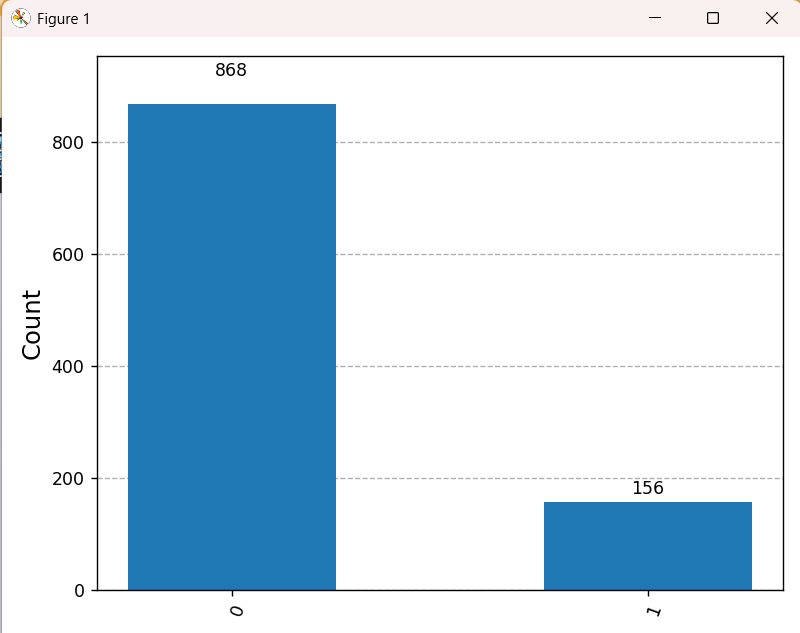
ヒストグラムの描画結果は、項 2.3.1. で予測した理論的な期待値と一致します。
第3章:まとめ
本記事では、Qiskitにおける\(\mathbf{U}3\) ゲートが、単なる複数の基本ゲートの組み合わせではなく、単一量子ビット操作の究極形であることを確認しました。
\(\mathbf{U}3\) ゲートは、\(\text{R}_X, \text{R}_Y, \text{R}_Z\) といった基本的な回転ゲートを包括・代替し、量子回路の最適化とゲート集積度の向上に不可欠な存在です。
特に、ゲートの集積度が課題となる実機での量子計算において、\(\mathbf{U}3\) ゲートを効果的に活用する知識は、高品質な量子プログラムを記述するための確かな基礎となるでしょう。
巻末付録
本編(2.3.)で \(U3\) ゲートが生成する測定確率の期待値を計算しました。
この付録では、任意の \(\boldsymbol{\theta}\)(シータ)の角度に基づいて、その理論値を自動で計算するための対話型Pythonプログラムを提供します。
以下のプログラムを実行することで、コンソール(コマンドライン)から角度を入力し、期待される確率を得ることができます。
import numpy as np
# --- 巻末付録の関数 ---
def calculate_u3_probability_interactive():
"""
ユーザーのコンソール入力(度数法)に基づき、U3ゲートの測定確率P(0)とP(1)を計算する。
"""
try:
# 1. コンソールからの入力を待機し、floatに変換
theta_degree = float(input("U3ゲートのターゲット角度 θ を入力してください (度数): "))
# 2. 度数をラジアンに変換
theta_rad = np.deg2rad(theta_degree)
# 3. 確率の計算: P(0) = cos^2(theta/2), P(1) = sin^2(theta/2)
p0 = np.cos(theta_rad / 2)**2
p1 = np.sin(theta_rad / 2)**2
# 4. 結果の出力
print(f"\n--- U3ゲート 測定確率の理論値計算結果 ---")
print(f"設定角度 θ: {theta_degree}°")
print(f"期待される確率 P(0) (理論値): {round(p0, 4)}")
print(f"期待される確率 P(1) (理論値): {round(p1, 4)}")
print(f"合計: {round(p0 + p1, 4)}")
except ValueError:
print("エラー: 有効な数値を入力してください。")
# --- メイン処理: 関数を呼び出し、コンソール入力を開始 ---
if __name__ == "__main__":
calculate_u3_probability_interactive()


コメント