前回記事では、現代数学の共通言語である「集合」の概念と、その厳密な表記法を学びました。
集合を箱(コンテナ)、要素を中身としてイメージしつつ、帰属関係 (\(\in\)) を用いて要素が集合に属することを論理的に表現する方法を確立しました。
しかし、多くの初学者が立ち止まるのは、集合を定義する段階ではありません。
それは、集合と集合の関係性を表す二つの記号が登場した瞬間です。
その二つの記号とは、「属する (\(\in\))」と「部分集合 (\(\subset\))」です。
これらは見た目も似ており、日常会話では「含む」という言葉で曖昧にされてしまいがちですが、集合論においては、これらが指し示す論理的な役割は全く異なります。
本記事の目標は、「属する (\(\in\))」と「部分集合 (\(\subset\))」の違いを完全に理解し、要素(中身)と集合(箱)という二つの役割を自在に使いこなせるようになることです。
今回の徹底比較を通じて、集合論における厳密な思考の基礎を完成させましょう。
目次
1. 記号 \(\in\) の再確認:要素と集合の関係
記号 \(\in\)(イプシロン)は前回記事で紹介済ですが、新たに登場する部分集合 (\(\subset\)) と比較するため、\(\in\) が持つ性質を改めて確認しておきましょう。
1.1. 帰属関係 (\(\in\)) の役割
記号 \(\in\)(イプシロン)が表す帰属関係(Membership)は、要素と集合の関係を定義します。
これは、「中身」と「箱」の関係と理解できます。
- \(\in\)の定義: 左辺には必ず要素(中身)が、右辺には必ず集合(箱)が来ます。
\(\text{要素} \in \text{集合}\)
例: \(A = \{5, 10, 15\}\) という集合があるとき、
- \(5 \in A\) (5 は 集合 \(A\) の要素である)
- \(12 \notin A\) (12 は 集合 \(A\) の要素ではない)
1.2. 要素は「箱」の中身である
ここで注意が必要なのは、\(\in\) の左辺にある限り、どのような対象であっても「要素」としての役割を果たすという点です。
例えば、集合 \(B\) が別の集合を要素として含む場合を考えてみましょう。
\(B = \{1, \{2, 3\}, 4\}\)
上記の集合 \(B\) の要素(中身)は3つです。
- \(1\) (数)
- \(\{2, 3\}\) (集合。これも一つのまとまりとして要素となる)
- \(4\) (数)
したがって、以下のような表記が成り立ちます。
- \(1 \in B\)
- \(\{2, 3\} \in B\)
- \(\{2\} \notin B\) 👈(\(\{2\}\) という集合は \(B\) の中には入っていない)
- \(2 \notin B\) 👈(\(2\) という単独の要素は \(B\) の中には入っていない)
\(\in\) の左辺に現れる \(\{2, 3\}\) は集合の表記ですが、\(B\) という箱にとっては一個の「要素」として扱われていることに注目してください。
2. 部分集合 (\(\subset\)) の定義:集合と集合の関係
まず、部分集合とは、ある集合のすべての要素(元)が、別の集合の要素でもある関係のことです。
なお、「空集合」も部分集合であることに注意が必要です。
2.1. 包含関係 (\(\subset\)) の役割
記号 \(\subset\)(サブセット)が表す包含関係(Inclusion)は、集合と集合の関係(集合同士の関係)を定義します。
これは、「箱」と「より大きな箱」の関係と理解できます。
- \(\subset\)の定義: 集合 \(A\) のすべての要素が、集合 \(B\) の要素でもあるとき、\(A\) は \(B\) の部分集合であるといい、以下の記号で表します。
\(\mathbf{A \subset B}\)
- チェックの視点(重要): \(\mathbf{A \subset B}\) のチェックでは、集合 \(A\) の要素を個別に取り出して(要素レベルで)、そのひとつひとつを \(B\) の要素リストと比較します。
- 論理的な定義: この関係は、厳密に以下の条件を満たすことを意味します。
任意の要素 \(x\) について、
\(x\) が \(A\) の要素ならば、必ず \(x\) は \(B\) の要素である
\(\in\) の左辺が個々の要素を指すのに対し、\(\subset\) は集合 \(A\) 全体を指します。
\(\in\) では「左辺は要素、右辺は集合」という制限があり、\(\subset\) は左辺も右辺も必ず集合でなければなりません。
2.2. 真部分集合 (\(\subset\)) と部分集合 (\(\subseteq\)) の区別
部分集合は、通常、二種類の表記法 「真部分集合」(\(\subset\)) と 「部分集合」 (\(\subseteq\)) に分けて考えられます。
「通常」という言い方をしているのには理由があり、文脈によっては、\(\subset\) の記号で \(\subseteq\) と同じ意味(等しい場合も含む)を表すこともあります。
しかし、厳密な議論では下線付きの \(\subseteq\) を用いて、等しい可能性を含めることを明確にするのが一般的です。
- 真部分集合 (\(\subset\)): \(A\) が \(B\) の部分集合であり、かつ \(A\) と \(B\) が等しくない場合に使われます。
- 例: \(\{1, 2\} \subset \{1, 2, 3\}\)
- 部分集合 (\(\subseteq\)): \(A\) が \(B\) の部分集合であり、\(A\) と \(B\) が等しい場合も含む最も一般的な関係です。
2.3. 空集合と全体集合の特殊な包含関係
空集合 (\(\emptyset\)) と全体集合 (\(U\)) は、\(\subset\) の定義から以下の特殊な関係を持ちます。
2.3.1. 空集合の包含
空集合 \(\emptyset\) は、任意の集合 \(A\) の部分集合となります。
\(\mathbf{\emptyset \subseteq A}\)
包含関係の定義は、「\(\emptyset\) の要素があれば、それは \(A\) の要素でもある」というものです。
しかし、\(\emptyset\) は要素を一つも持ちません。
要素がないという事実によって、論理的な条件は自動的に満たされ(真となり)、\(\emptyset \subseteq A\) は成立すると結論づけられます。
これは、数学的論理の「空虚な真 (Vacuous Truth)」というルールに基づいた考え方です。
逆の表現をすれば、包含関係が成立しないためには、「\(\emptyset\) の要素 \(x\) の中で、 \(A\) に含まれていないもの」が最低一つ存在する必要があります。
しかし、\(\emptyset\) には要素が一つも存在しないため、この「成立しないための条件」を満たすことができません。
よって、\(\emptyset \subseteq A\) は論理的に常に成立すると結論づけられます。
なお、補足として、集合 \(A\) が空集合でない場合(\(A \neq \emptyset\))、つまり\(\emptyset\) は \(A\) の真部分集合(\(\mathbf{\emptyset \subset A}\))の関係が成り立ちます。
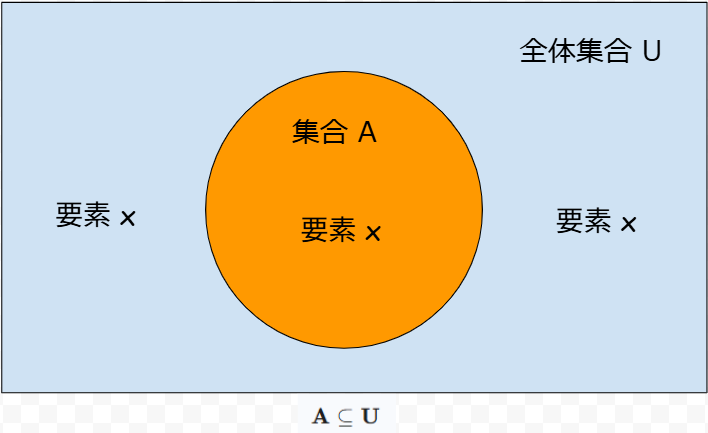
2.3.2. 全体集合の包含
任意の集合 \(A\) は、必ず全体集合 \(U\) の部分集合となります。
\(\mathbf{A \subseteq U}\)
まず、全体集合 \(U\) が議論の文脈でどのように定義されているかを復習すると、以下の通りです。
- 定義: 全体集合 \(U\) は、議論の対象となるすべての集合の要素を、漏れなくすべて含む集合として設定されます。
この全体集合 \(U\) の定義によって、現在対象としている集合 \(A\) の要素 \(x\) は、その議論の枠組み(Universe of Discourse)の中で考えられているため、要素 \(x\) は、最初から \(U\) の要素であると結論づけられます。
まとめ
本記事では、集合論における二つの基本的な関係記号、要素の所属を示す \(\mathbf{\in}\) と、集合の包含を示す \(\mathbf{\subset}\)(または \(\mathbf{\subseteq}\))の正しい使い分けを解説しました。
最も重要なポイントは、記号が両辺に要求する「対象」の違いを理解することです。
この二つの記号を混同せず使いこなすことが、集合論を学ぶ上で最初のハードルとなりますので、納得できるまで復習してみてください。


コメント