指数関数の世界 ～有理数から実数への拡張

前回までで、指数 \(x\) は整数から分数へと拡張され、すべての有理数 \(p\) に対して \(a^p\) を矛盾なく定義し、統一された指数法則のもとで計算できるようになりました。

これにより、\(a^2\) や \(a^{\frac{1}{2}}\) といった計算はマスターしましたが、まだ一つ、数直線上に「穴」が残っています。無理数です。

関数 \(y = a^x\) のグラフを考えるとき、このグラフは途切れることなく、滑らかで連続していなければなりません。
しかし、\(\sqrt{2}\) や \(\pi\) のような無理数を指数に持つ値が定義されていない状態では、グラフは連続しません。

今回の記事のテーマは、この「穴」を埋めることです。
有理数で囲まれた極限操作を利用して無理数指数（実数指数）を定義し、すべての実数 \(x\) に対して成立する指数関数 \(y=a^x\) の世界を完成させましょう。

第1章：無理数指数と実数指数：連続性のための拡張

1.1. 無理数指数 \(a^{\sqrt{2}}\) の定義方法

前回までで指数は有理数全体に拡張されましたが、指数関数 \(y=a^x\) を連続したグラフとして定義するためには、 \(\sqrt{2}\) や \(\pi\) のような無理数指数を定義する必要があります。

無理数とは循環しない無限小数であり、分数指数のように単純な代数的操作で定義することはできません。
そこで、極限（限りなく近づく操作）の考え方を利用して無理数指数を定義します。

具体的な例として、\(2^{\sqrt{2}}\) の定義を考えてみましょう。

\(\sqrt{2}\) はおよそ \(1.41421356…\) という無限小数です。
この \(\sqrt{2}\) に限りなく近づく有理数の列（近似値）を利用します。

\(\sqrt{2}\) より小さい有理数 \(p_n\) (下からの近似)	\(\sqrt{2}\) より大きい有理数 \(q_n\) (上からの近似)
\(p_1 = 1.4\)	\(q_1 = 1.5\)
\(p_2 = 1.41\)	\(q_2 = 1.42\)
\(p_3 = 1.414\)	\(q_3 = 1.415\)
\(p_4 = 1.4142\)	\(q_4 = 1.4143\)
\(\dots\)	\(\dots\)

上記の有理数の列を使って、底 \(a=2\) の指数 \(2^x\) を計算すると、次の表のようになります。

下からの有理数指数 \(2^{p_n}\)	上からの有理数指数 \(2^{q_n}\)
\(2^{1.4} \approx 2.639\)	\(2^{1.5} = 2.828\)
\(2^{1.41} \approx 2.657\)	\(2^{1.42} \approx 2.675\)
\(2^{1.414} \approx 2.664\)	\(2^{1.415} \approx 2.666\)
\(2^{1.4142} \approx 2.6651\)	\(2^{1.4143} \approx 2.6653\)
\(\dots\)	\(\dots\)

\(p_n\) が \(\sqrt{2}\) に近づくにつれて \(2^{p_n}\) の値は増加し、 \(q_n\) が \(\sqrt{2}\) に近づくにつれて \(2^{q_n}\) の値は減少します。
そして、この二つの値の列は、ある一つの決まった実数値に限りなく近づいていきます。

この挟み撃ちの操作によって、\(2^{\sqrt{2}}\) の値は次のように極限として定義されます。

• \(\lim\)：「Limit（極限）」の略です。数学では、「限りなく近づく」操作を表す重要な記号です。
• \(n \to \infty\)：「\(n\) を「無限大」（限りなく大きな数）にする」という意味です。ここでは、近似計算を無限に続けることを意味します。

つまり、有理数指数 \(2^{p_n}\) が限りなく近づく値を、無理数指数 \(2^{\sqrt{2}}\) の値として定義するということです。

1.2. 実数指数の定義の完成

極限による定義は、すべての底 \(a>0\) とすべての無理数 \(x\) に対して適用できます。

この定義によって指数 \(x\) は実数指数としても扱えるようになり、実数全体を定義域とする指数関数 \(y=a^x\) を本格的に考える土台が整いました。

第2章：指数関数 \(y = a^x\) のグラフと単調性

2.1. 指数関数とは

指数関数 (Exponential Function) とは、底 \(a\) が定数（\(a>0, a \neq 1\)）であり、指数 $x$ が変数である関数を指します。

ここで、底 \(a\) に「\(a>0\) かつ \(a \neq 1\)」という条件がつく理由を再確認しておきましょう。

• \(a>0\) である理由：
  • 底 \(a\) が負またはゼロとすると、指数 \(x\) が有理数（例えば \(\displaystyle \frac{1}{2}\) や \(\displaystyle \frac{1}{4}\)）のときに実数値が定義できない場合があるため、定義域を実数全体にするために \(a\) は正と定めます。
  • 例：\((-2)^{\frac{1}{2}} = \sqrt{-2}\) は実数ではない
• \(a \neq 1\) である理由：
  • \(a=1\) とすると、\(y=1^x = 1\) です。これは、常に一定値をとる定数関数（横一直線のグラフ）となり、指数関数の特徴的な性質を持たないため除外します。

2.2. グラフの形状を決定する「底 \(a\)」の役割

指数関数 \(y=a^x\) のグラフは、底 \(a\) の値によって2つのパターンに分かれます。
このグラフの形状が、後の指数不等式を解く鍵となります。

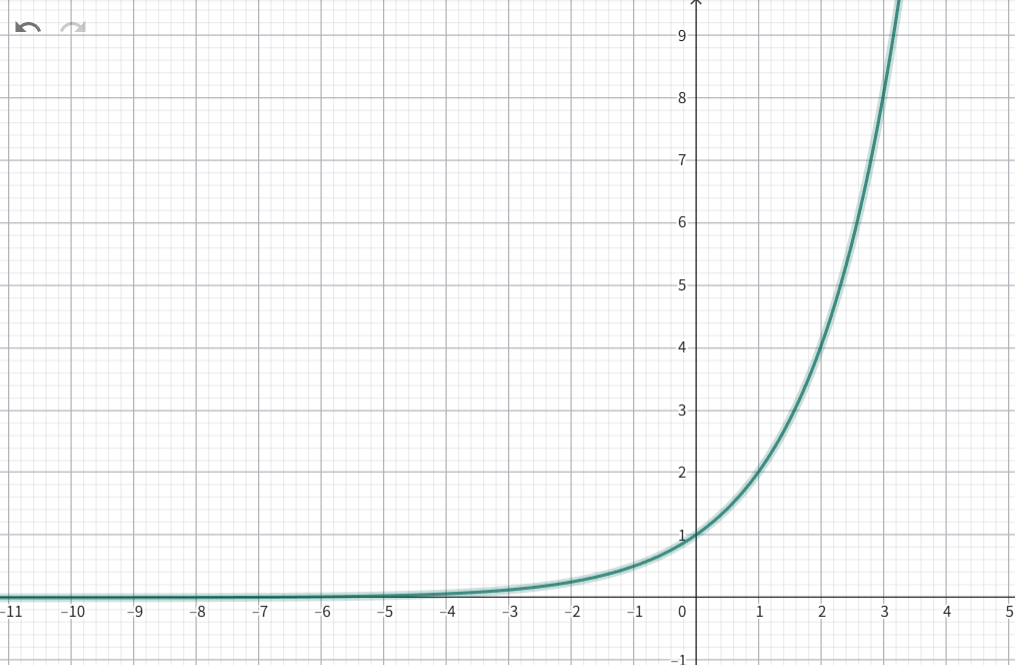
パターン1：底 \(a\) が 1 より大きい場合 (\(a > 1\))

例として、\(a=2\) の場合 (\(y = 2^x\)) を考えます。

\(x\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)
\(y=2^x\)	\(\displaystyle \frac{1}{4}\)	\(\displaystyle \frac{1}{2}\)	\(1\)	\(2\)	\(4\)	\(8\)

• \(x\) が増加するにつれて、\(y\) の値も急激に増加します。
• このとき、関数 \(y=a^x\) は増加関数（単調増加）であるといいます。

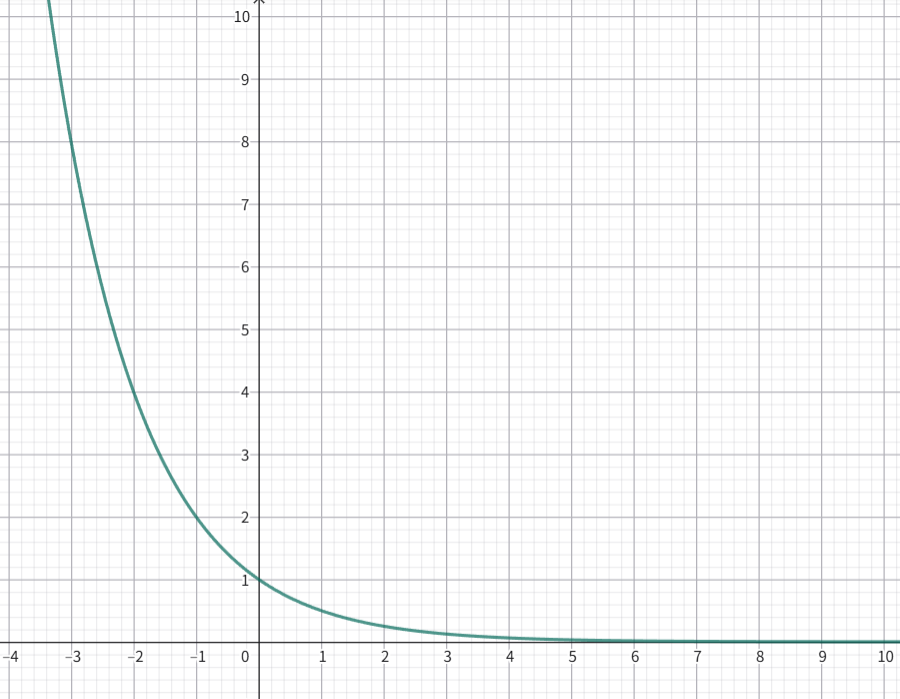
パターン2：底 \(a\) が 0 より大きく 1 より小さい場合 (\(0 < a < 1\))

続いて、\(\displaystyle a = \frac{1}{2}\) (\(a = 0.5\)) の場合を考えます。（例：\(\displaystyle y = \left(\frac{1}{2}\right)^x = 2^{-x}\)）

\(x\)	\(-3\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)
\(\displaystyle y = \left(\frac{1}{2}\right)^x\)	\(8\)	\(4\)	\(2\)	\(1\)	\(\displaystyle \frac{1}{2}\)	\(\displaystyle \frac{1}{4}\)

• \(x\) が増加するにつれて、\(y\) の値は減少します。
• このとき、関数 \(y=a^x\) は減少関数（単調減少）であるといいます。

2.3. 指数関数のグラフの比較

上のグラフが示すように、\(y=a^x\) のグラフは、底 \(a\) の値にかかわらず、次の共通した特徴を持っています。

• 定点 (Fixed Point) を通る： すべてのグラフは必ず点 \((0, 1)\) を通ります。なぜなら、任意の底 \(a\) に対して \(a^0 = 1\) だからです。
• 定義域 (Domain)： \(x\) はすべての実数をとります。（実数全体）
• 値域 (Range)： \(y\) は必ず正の値をとります。 \(y > 0\) （正の実数全体）
• 漸近線 (Asymptote)：グラフは \(x\) 軸（\(y=0\)）に限りなく近づきますが、交わることはありません。この \(x\) 軸が漸近線ぜんきんせんです。

このグラフの単調性（\(a>1\) なら増加、 \(0<a<1\) なら減少）は、後の指数不等式を解く上で極めて重要な知識となります。

第3章：指数関数の重要な性質のまとめ

3.1. 基本的な範囲と構造

2.2. のグラフが示すように、\(y=a^x\) のグラフは、底 \(a\) の値にかかわらず、次の共通した特徴を持っています。

• 定点 (Fixed Point) を通る： すべてのグラフは必ず点 \((0, 1)\) を通ります。なぜなら、任意の底 \(a\) に対して \(a^0 = 1\) だからです。
• 定義域 (Domain)： \(x\) はすべての実数をとります。（実数全体）
• 値域 (Range)： \(y\) は必ず正の値をとります。 \(y > 0\) （正の実数全体）
• 漸近線 (Asymptote)：グラフは \(x\) 軸（\(y=0\)）に限りなく近づきますが、交わることはありません。この \(x\) 軸が漸近線ぜんきんせんです。

3.2. 単調性と一対一対応の性質

次の2つの性質は、グラフの形状から導かれる「方程式」・「不等式」を解く上で重要です。

1. 単調性（増加・減少）
   • \(a > 1\) ： 単調増加関数（\(x_1 < x_2 \Rightarrow a^{x_1} < a^{x_2}\)）
     \(\Longrightarrow \) 不等号の向きは変わらない
   • \(0 < a < 1\) ： 単調減少関数（\(x_1 < x_2 \Rightarrow a^{x_1} > a^{x_2}\)）
     \(\Longrightarrow \) 不等号の向きが反転する
2. 一対一対応 (One-to-One Mapping)
   • 異なる \(x\) の値には、必ず異なる \(y\) の値が対応します（水平線とグラフの交点は一つ）。
   • この性質は、「\(a^{x_1} = a^{x_2}\) ならば、$x_1 = x_2$ である」という指数方程式の解法の根拠となります。

3.2. 指数法則の再確認

これまでの記事で学んだ指数法則は、指数が整数、有理数と拡張されてきましたが、第1章で無理数指数が定義されたことにより、すべての実数 \(x, y\) に対して成立することが保証されます。

1. \(a^x a^y = a^{x+y}\)
2. \(\displaystyle \frac{a^x}{a^y} = a^{x-y}\)
3. \((a^x)^y = a^{xy}\)
4. \((ab)^x = a^x b^x\)
5. \(\displaystyle \left(\frac{a}{b}\right)^x = \frac{a^x}{b^x}\)

第4章：指数方程式と指数不等式

指数関数 \(y = a^x\) の単調性（増加または減少）と一対一対応の性質を利用することで、指数部分に変数が含まれる方程式や不等式を解くことができます。

4.1. 指数方程式の解法

指数方程式とは、\(a^x = b\) のように、指数に変数が含まれる方程式です。
\(a^{f(x)} = a^{g(x)}\) や、置き換えによってこの形に帰着できる方程式のように、指数に変数が含まれるものもあります。

解法のステップは次の通りです。

1. 底の統一： 両辺の底 \(a\) を同じ値に統一します。
2. 指数の比較： 「\(a^{x_1} = a^{x_2}\) ならば、\(x_1 = x_2\) である」という一対一対応の性質を利用し、指数同士を比較して方程式を解きます。

4.1.1. 【例題】基本的な指数方程式

方程式 \(8^x = 4^{x+1}\) を解いてみましょう。

1. 底の統一： 両辺の底を \(2\) に統一します。
   • \(8 = 2^3\) なので、 \(8^x = (2^3)^x = 2^{3x}\)
   • \(4 = 2^2\) なので、 \(4^{x+1} = (2^2)^{x+1} = 2^{2(x+1)} = 2^{2x+2}\)
2. 指数の比較： \(2^{3x} = 2^{2x+2}\) となったので、指数同士を比較します。
   • \(3x = 2x + 2\)

したがって、答えは \(x = 2\) となります。

4.2. 指数不等式の解法

指数不等式とは、指数に変数が含まれる不等式です。
指数方程式とは異なり、底 \(a\) の単調性によって、不等号の向きが変わることに注意が必要です。

解法のステップは次の通りです。

1. 底の統一： 両辺の底 \(a\) を同じ値に統一します。
2. 底による単調性の確認： 底 \(a\) が \(1\) より大きいか小さいかを確認します。
3. 指数の比較： 指数同士を比較しますが、底の範囲に応じて不等号の向きを変えます。

4.2.1. 【例題1】底が \(a > 1\) の指数不等式

不等式 \(3^{x} < 81\) を解いてみましょう。

1. 底の統一： \(81 = 3^4\) なので、 \(3^x < 3^4\)
2. 単調性の確認： 底 \(a=3\) は \(3 > 1\) なので、増加関数です。
3. 指数の比較： 不等号の向きはそのまま。

したがって、答えは \(x < 4\) となります。

4.2.2. 【例題2】底が \(0 < a < 1\) の指数不等式

不等式 \(\displaystyle \left(\frac{1}{2}\right)^x \le \frac{1}{16}\) を解いてみましょう。

1. 底の統一： \(\displaystyle \frac{1}{16} = \left(\frac{1}{2}\right)^4\) なので、 \(\displaystyle \left(\frac{1}{2}\right)^x \le \left(\frac{1}{2}\right)^4\)
2. 単調性の確認： 底 \(\displaystyle a=\frac{1}{2}\) は \(\displaystyle 0 < \frac{1}{2} < 1\) なので、減少関数です。
3. 指数の比較： 不等号の向きを反転させます。

したがって、答えは \(x \ge 4\) となります。

終わりに：指数の理解が拓く「対数」への扉

全3回に渡った「指数」の探求は、本記事を持って終幕です。

最初は「同じ数を何回掛けるか」という素朴な数え上げから、指数の学習は始まりました。
それが、マイナスの世界、分数の世界、そしてついには無理数を含む「実数」という広大な世界へと拡張され、さらに単なる「計算の道具」から、連続的な変化を記述する「関数」へと指数を昇華させるに至りました。

• 指数法則： 数の範囲が広がっても揺るがない、指数の世界の普遍的なルール。
• 単調性： グラフの動きを予測し、不等式を解くための性質。

次なるステップ：対数（log）の世界へ

さて、指数を完全にマスターした読者の目の前には、新しい扉が現れています。それが「対数（logarithm）」です。

指数が「\(a\) を \(x\) 乗したら何になるか？」という問いに答えるものだとしたら、対数はその逆、つまり「\(a\) が \(M\) になるには何乗すれば良いか？」という問いに答えるための概念です。

指数のシリーズを最後まで読み切ったあなたなら、必ず対数の本質も掴み取れることでしょう。
それでは、「対数シリーズ」でお会いできる日を楽しみにしています。