【統計①】平均だけでは不十分？Python、中央値・最頻値のコラボでデータの特徴を「見える化」

「平均点くらいだったから、まあ普通かな」
このように私たちは「平均」という言葉を、その集団の「普通」や「真ん中」を指すものとして日常的に使っています。

しかし、前回の記事で学んだ「期待値（平均報酬）」は、あくまで「膨大な試行を繰り返した時の理論的な境界線」でした。
現実の世界に存在する、回数が限られたデータ群を分析する場合、平均値だけを見ていると、とんでもない見当違いをしてしまう場合があります。

今回は、Pythonのライブラリ「Pandas」を使い、平均・中央値・最頻値という3つの指標をコラボレーションさせることで、裏側に隠されたデータの特徴を浮き彫りにする方法を学びます。

第1章：平均値が「見ているもの」

なぜ、平均値だけでは不十分なのでしょうか。
それは平均値が「外れ値（極端に大きい、または小さい値）」に引きずられるという、統計上の強力なバイアス（偏り）を持っているからです。

統計において「平均値」は最もポピュラーな指標ですが、万能ではないことを認識しておく必要があります。
平均値が得意なのは「グループ全体の総量を均等に割り振った時の値」を出すことであり、データの「分布の偏り」までは教えてくれないからです。

例えば「平均年収」を考えてみましょう。
ある10人からなるグループで、年収300万円の人が9人、年収1億円の人が1人でした。
すると、平均年収は1,270万円になります。

この1,270万円という数字は、決して嘘ではありません。
しかし、この数字から「この集団の標準的な生活水準」を想像しようとすると、実態とのズレが生じます。
ここで、平均値が計算の過程で削ぎ落としてしまった「位置」や「頻度」の情報を補完するのが、今回スポットを当てる2つの指標です。

第2章：中央値・最頻値が「映し出すもの」

平均値が「全体を均ならす」指標であるのに対し、中央値と最頻値は、データの内部構造にある「順位」や「密度」に着目します。
これらを詳しく知ることで、平均値だけでは見えなかったデータの特徴が浮かび上がってきます。

2.1. 中央値（Median）：データの「真ん中の順位」にフォーカス

中央値は、データを昇順（小さい順）または降順（大きい順）に並べたときに、ちょうど真ん中に位置する値のことです。

算出には以下のルールがあります。

• データが奇数個の場合：完全に真ん中に位置する一人の値。
  • 例：[1, 3, 10] → 中央値は「3」
• データが偶数個の場合：真ん中に並ぶ「二人の平均値」。
  • 例：[1, 3, 5, 10] → \((3 + 5) \div 2 = 「4」\)が中央値

中央値の最大の特徴は、「外れ値に対する圧倒的な強さ」です。
10人の中に1人だけ年収1億円の大富豪がいても、中央値は真ん中付近の人の値しか見ません。
1億円という数値そのものは計算に使われず、あくまで「1番リッチな人」という「順位」として処理されるため、「集団の真ん中の順位にいる人はどれくらいか」という位置的な実態を正確に映し出します。

2.2. 最頻値（Mode）：データの「最大勢力」を射抜く

最頻値は、データの中で最も頻繁に登場する値、つまり「出現回数が最も多い値」です。

• 算出方法：各データがいくつあるかを数え、カウントが最大のものを選びます。
• 注意点：カウントが同率1位となり、最頻値が「2つ以上」存在することもあります。
  • 中央値のように平均を算出することはなく、該当した複数データを最頻値として許容します。
  • 最頻値が複数存在することを統計学では「多峰性（たほうせい）」がある、と言います。

平均値は全体を薄く引き伸ばし、中央値がセンターラインを引くのに対し、最頻値は「最もありふれた存在はどこか」という一点を射抜きます。
年収の例で言えば、平均値が1億円プレイヤーに引きずられて1,270万円になったとしても、最頻値は「最もありふれた存在」である300万円を指し示します。

2.3. なぜ、使い分けが必要なのか

データが左右対称な山型（正規分布）をしていれば、これら3つの値は一致します。
しかし、現実のデータは往々にして左右どちらかに偏っています。

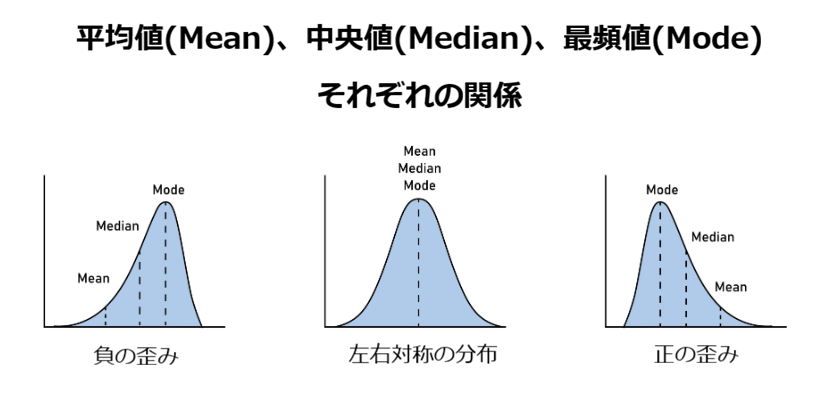
• 平均値：全体の「規模感」を測る。
• 中央値：真ん中の順位の「位置」を測る。
• 最頻値：最大勢力の「密度」を測る。

この3つの視点をコラボレーションさせることで、「このデータは一部の例外に引っ張られている」といった、データの「歪み」を正しく認識できるようになります。

第3章：Python+Pandasで「3つの代表値」を算出・比較する

ここまで見てきたように、中央値や最頻値を正確に求めるには「すべてのデータを並べ替える」「すべての出現回数をカウントする」という全量把握の手順が欠かせません。
データが10個程度なら手計算も可能ですが、これが1,000個、10,000個… と増えた場合、手作業で処理するのは極めて困難ですしミスも起こるでしょう。それに、考えただけで途方に暮れてしまいますよね。

そこで絶大な威力を発揮するのがプログラミングです。
Pythonと、そのライブラリ「Pandas」を使えば、どれほど大量のデータであっても、わずか一行ずつの命令で、正確にこれらの値を導き出すことができます。

本章では、実際にコードを動かしながら、平均値・中央値・最頻値の「ズレ」を数値として確かめていきましょう。

3.1. Pandasのインストールと準備

Pandasを利用するためには、まず自身のPython環境にインストールする必要があります。
PythonやIDE（統合開発環境）をまだお持ちでない方は、こちらの記事を参考に環境構築を完了させてください。

Pandasのインストールは、ターミナル（またはコマンドプロンプト）で以下のコマンドを実行します。

pip install pandas

インストールが完了したら、Pythonスクリプトの冒頭で import pandas as pd と記述することで、Pandasの強力な機能が使用可能になります。

3.2. 基本的な統計量の算出メソッド

Pandasでは、列データ (Series) や表データ (DataFrame) に対して、以下のメソッドを呼び出すだけで計算が完了します。

• 平均値：.mean() すべての値を足して数で割った値。
• 中央値：.median() データを並べ替えて真ん中の順位を特定した値。
• 最頻値：.mode() 出現頻度をカウントした値。
  • ※ 複数の値が返る可能性があるため、結果はリストのような形式（Series）で出力されます。

3.3. 【コーディング】年収データで「3つの値」のズレを確認する

まずは計算に使用するデータを作成しましょう。
300万円台を中心としたリアルなバラつきの中に、一人だけ1億円プレイヤーが混ざっているケースを想定します。

新規ファイル analyze_income.py を作成し、以下のプログラムをコーディングしてください。

import pandas as pd

# データの作成（単位：万円）
# 300万円台を中心にバラつかせ、一人だけ1億円（10,000万円）を投入
data = [280, 300, 310, 320, 320, 340, 350, 380, 400, 10000] 
df = pd.DataFrame(data, columns=['income'])

# 3つの代表値を算出
mean_val   = df['income'].mean()
median_val = df['income'].median()
mode_series = df['income'].mode()

# 結果の表示
print("--- 年収データの統計量 ---")
print(f"平均値: {mean_val:>5.0f} 万円")
print(f"中央値: {median_val:>5.0f} 万円")
print(f"最頻値: {mode_series[0]:>5.0f} 万円")

3.4. 実行結果の分析：数値からデータの「歪み」を読み解く

3.3. のプログラムを実行すると、以下の結果が表示されるはずです。

--- 年収データの統計量 ---
平均値:  1300 万円
中央値:   330 万円
最頻値:   320 万円

この結果から、次のことが明確にわかります。

1. 「平均値」だけでは当てにならない： 平均値が中央値や最頻値の約4倍にも膨れ上がっています。これは、集団の大部分が300万円台にいるにもかかわらず、少数の（あるいは一人の）極端に大きな値が全体の平均を無理やり引き上げていることを示しています。
2. 「右裾を引く分布（正の歪み）」である： 「最頻値 < 中央値 < 平均値」という順番で値が大きくなっています。この力関係が成立しているときは、グラフを描くと必ず右側に長く裾を引く形になります。
3. 「中央値」と「最頻値」が実態に近い： 中央値と最頻値が近い値を示していることから、この集団の「ボリュームゾーン」および「真ん中の順位」は300万円台前半に固まっていることが分かります。

3.5. コードの仕組み：DataFrameとSeries

実行に成功したところで、今回使用したPandasの主要な概念を整理しておきましょう。

• pd.DataFrame(data, columns=['income'])
  • リスト形式のデータを、Pandas専用の「表形式（DataFrame）」へ変換しています。Pandasで高度な統計計算を行うためには、この「表の形」に整えるステップが必須となります。columnsで列に名前を付けることで、大量のデータの中から特定の項目（今回は’income’）を指定して計算できるようになります。
• df['income']
  • 表（DataFrame）から特定の列だけを抜き出したものを「Series（シリーズ）」と呼びます。今回の .mean() などの計算は、このSeriesに対して行われています。
• mode_series[0]
  • 平均値や中央値は必ず「1つ」に決まりますが、最頻値は「同率1位」が複数存在する可能性があります。そのため、.mode() の結果は常にリストのような形式で返ってきます。今回はその中の「1番目（インデックス0）」を取り出す指定をしています。

【重要】最頻値についての補足

今回のサンプルデータでは 320 万円が唯一の最頻値だと分かっていたため、便宜上 [0] で最初の1つだけを取り出し、プログラムを簡単にしました。

しかし、実務では「最頻値が複数存在する」ケースは珍しくありませんし、そうでなかったとしても、「最頻値が複数存在する」前提でプログラムすべきです。

# 最頻値をすべてカンマ区切りで表示させる例
modes = df['income'].mode().tolist()
print(f"最頻値: {', '.join(map(str, modes))} 万円")

このように「リストとして受け取り、すべてを処理する」という考え方を持つことで、偏ったデータが来ても、最大勢力を見落とすことなく捉えることができます。

第4章：Matplotlibでデータの「歪み」を可視化する

「データの歪み」を目で見て実感するため、グラフ（ヒストグラム）を描画しましょう。
そこに平均値・中央値・最頻値を線として書き込むことで、統計指標の正体がクリアに見えてきます。

4.1. ヒストグラム描画と日本語化の準備

Pythonでグラフを扱うための定番ライブラリ「Matplotlib」をインストールします。

pip install matplotlib japanize-matplotlib

4.2. 【コーディング】統計値を描き込んだヒストグラムの作成

第3章で作成したコードを拡張して、ヒストグラムと3本の垂直線を描画するプログラム visualize_income.py を作成します。
（差分を判断できる方は、既存のプログラム analyze_income.py を編集する方法でもOKです）

import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib # 日本語化ライブラリをインポート

# 1. データの作成
data = [280, 300, 310, 320, 320, 340, 350, 380, 400, 10000]
df = pd.DataFrame(data, columns=['income'])

# 2. 各統計量の算出
mean_val = df['income'].mean()
median_val = df['income'].median()
mode_val = df['income'].mode()[0]

# 3. グラフの描画
plt.figure(figsize=(10, 6))
# binsを細かくしすぎると「山」が見えにくいため、今回は範囲を絞って描画
plt.hist(df['income'], bins=100, color='skyblue', alpha=0.7, label='年収の分布')

# 4. 統計量を表す垂直線を引く
plt.axvline(mean_val, color='red', linestyle='dashed', linewidth=2, label=f'平均値: {mean_val:.0f}万')
plt.axvline(median_val, color='green', linestyle='dashed', linewidth=2, label=f'中央値: {median_val:.0f}万')
plt.axvline(mode_val, color='orange', linestyle='dashed', linewidth=2, label=f'最頻値: {mode_val:.0f}万')

# 5. 日本語ラベルの設定
plt.title('年収データにおける「平均・中央・最頻」のズレ')
plt.xlabel('年収（万円）')
plt.ylabel('人数（頻度）')
plt.legend() # 凡例を表示
plt.grid(axis='y', alpha=0.3) # 横線を薄く入れる
plt.show()

4.3. 実行結果のヒストグラムを読み取る

プログラムを実行すると、右側に長く伸びた裾（一人の1億円プレイヤー）のせいで、山が左側に極端に寄ったヒストグラムが表示されます。

• 緑とオレンジの線（中央・最頻値）：多くのデータが集まっている「山」にしっかりと寄り添っています。
• 赤い線（平均値）：多くの人がいる「山」から離れ、一人ぼっちで右側に立っています。

総まとめ

本記事では、日常的に使われる「平均」という言葉の裏側に隠された罠から、Pythonを用いたデータ分析の入り口までを体験しました。
最後に、データと向き合うための重要なポイントを振り返りましょう。

1. 平均・中央・最頻の「三位一体」で見る
   一つの指標（平均値）だけに頼ると、少数の極端なデータによって真実が隠されてしまいます。データの形を正しく捉えるには、常にこの3つをセットで確認する習慣が大切です。
   • 平均値：データ全体を「平らに均ならした」値。集団全体の総量を把握するのに適しています。
   • 中央値：並び順の「ど真ん中」。外れ値に左右されない「一般的な感覚」に近い値です。
   • 最頻値：出現頻度の「ピーク」。最もありふれた、ありのままの実態を指し示します。
2. 指標のズレがデータの「形」を教えてくれる
   今回、計算結果は 「最頻値 < 中央値 < 平均値」 という順に並びました。この順序を確認するだけで、わざわざグラフを描かなくても「このデータには、平均を大きく引き上げる超富裕層が一部に存在する（右裾を引く分布である）」という構造を読み解くことができます。
3. Pythonという「確かな目」を持つ
   手計算では数えることすら不可能な膨大なデータも、Python（Pandas / Matplotlib）を使えば、一瞬で正確な統計量へと変換し、目に見える形に可視化できることが分かりました。
   • Pandas：全量データを正確に捌き、計算ミスを防ぐ。
   • Matplotlib：直感に訴えかけるヒストグラムを描画する。

「平均値が高いから、この集団はリッチだ」という単純な結論で終わらせず、その背後にある構造まで見抜く力「データリテラシー」をマスターする第一歩になれば幸いです。