前回の記事では、複雑な環境構築を乗り越え、無料のIBM Quantum環境へのアクセスを確立しました。
さらに、記念すべき最初の量子回路(重ね合わせを作る「量子版 Hello World」)を実装から実行まで完遂させ、量子プログラミングの第一歩を踏み出しました。
今回から、いよいよ本格的な「量子の言語」を学びます。
量子回路は、線(量子ビット)と箱(量子ゲート)で描かれる独自の文法を持っています。
今回のゴールは、この言語を読み書きできるように、基本的な量子ゲート(量子の単語)の役割をマスターし、量子回路図(量子の文法)とコードを結びつけることです。
この知識がなければ、今後の量子アルゴリズムの理解は困難です。
早速、量子の単語帳を開きましょう!
目次
第1章:量子プログラミングの基本用語の復習
まず、このシリーズでの用語の呼び方と意味を再確認します。
| 用語 | 意味 |
|---|---|
| 量子ビット (Qubit) | 量子状態(|0⟩ または |1⟩、あるいは重ね合わせの状態)を保持する単位。 |
| 量子ゲート | 量子ビットの状態を操作する命令(量子の単語)。 |
| 量子回路図 | 量子ビットの線の上に、量子ゲートを時系列で並べた図(量子の文法)。 |
|0⟩、|1⟩といった表記は、「ケット」と呼ばれる記号です。
この記号は一見難解に見えますが、恐れる必要はありません。これは単に、量子ビットの「状態」に付けられた特別なニックネームのようなものです。
- |0⟩ は、「この量子ビットは現在0の状態に確定しているよ」という名前(状態ベクトル)を表します。
- |1⟩ は、「この量子ビットは現在1の状態に確定しているよ」という名前(状態ベクトル)を表します。
現段階では複雑な数式を気にせず、「量子状態の住所(アドレス)」のようなものだと理解しておけば、量子プログラミングを進める上では問題ありません。
第2章:量子回路図の読み方:文法ルール
① 量子回路図とは
量子回路図は単なる図ではなく、量子プログラムを視覚的に表現するための国際的な「設計図」であり「共通言語」です。
①-1. 量子回路図の3つの目的
量子回路図が存在する目的は、主に次の3点に集約されます。
- 設計図・実装のブループリント:
量子回路図は、意図した計算を量子コンピュータに実行させるための明確な指示書として機能します。- プログラムの視覚化:PythonのQiskitコード(例:
circuit.h(0),circuit.cx(0, 1)) は、実行される順番に時系列で図として表現されます。これにより、コードの機能や意図を即座に視覚的に把握できます。 - 実機への命令:量子回路図は、最終的に量子コンピュータの制御システム(コンパイラ/トランスパイラ)に送られ、実機の物理的な操作(パルス)へと変換されます。回路図は、この複雑な変換プロセスの入口となるのです。
- プログラムの視覚化:PythonのQiskitコード(例:
- 普遍的なコミュニケーションツール:
量子回路図は、プログラミング言語(Python, Julia, C++など)やプラットフォーム(IBM, Google, Amazonなど)に依存しない、量子分野の国際的な共通言語です。- モデリング言語:量子回路図は通常のプログラミングにおける UML(統一モデリング言語)が果たす役割と本質的に同じです。中でも特にアクティビティ図やシーケンス図に近い役割を持っています。
- アイデアの共有:研究者や開発者は、数式や複雑なコードの羅列ではなく、回路図を見せることで、複雑な量子アルゴリズム(例: ドイッチュ・ジョサ、ベル状態)の構造を瞬時に共有し、議論できます。
- 論文・教科書:量子アルゴリズムに関するすべての論文や教科書は、その計算の核となる部分を回路図で表現します。コードよりも普遍的で、簡潔な表現方法だからです。
- ロジックのチェックとデバッグ補助:
回路図は、アルゴリズムの論理的な流れをチェックし、エラーを見つけ出すための強力なデバッグツールとしても機能します。- 流れの追跡:量子ビットの線(\(q_0, q_1\) など)に沿って、ゲートがどのように状態を変化させているか(例: Hで重ね合わせ、CNOTで条件付き操作)を、ステップ・バイ・ステップで追跡できます。
- 論理的な整合性:コードを書く際に、意図せず間違ったインデックスを指定してしまうミスを防ぐのに役立ちます。回路図を見れば、制御ビットとターゲットビットが正しいかが一目瞭然だからです。
② 量子回路図の基本ルール
- 時間軸は左から右:図の左側がプログラムの開始(初期状態)で、右側に向かって時間が進み、操作が適用されます。
- 線は量子ビット:横線一本一本が、独立した量子ビットを表します。線の上部から 0,1,2,… とインデックスが振られます。
- 箱は量子ゲート:線の上に描かれた箱やマークが、その量子ビットに適用される量子ゲートです。
③ 回路図が使われるフェーズ
量子回路図の役割は、大きく「実機へのジョブ送信前(設計・デバッグ)」と「ジョブ送信後(検証・分析)」の2つのフェーズに分けられます。
③-1. ジョブ送信前:設計とデバッグ(主な目的)
実機へのジョブ送信前のフェーズでは、回路図は「プログラムによる命令を視覚的に表現するもの」として、まさに主要な役割を果たします。
| 役割 | 説明 |
|---|---|
| 命令の視覚化 | Qiskitコードで定義したゲート操作(例: circuit.h(), circuit.cx())を、時系列に沿った論理的な設計図として表現します。 |
| 論理の検証 | アルゴリズムの論理的な流れが正しいかを確認するのに使われます。 |
| トランスパイルの入力 | この論理回路図が、実機が理解できる物理的なゲート命令へ変換(トランスパイル)されるための出発点となります。 |
③-2. ジョブ送信後:検証と分析(二次的な目的)
ジョブ送信後、実機が実際に実行するのはパルス(マイクロ波)の波形であり、回路図ではありませんが、結果を分析するために回路図を再び登場させることはできます。(あくまでも二次的な目的であり、主要目的はジョブ送信前の設計図としての働きです)
| 役割 | 説明 |
|---|---|
| トランスパイル後の確認 | 実機にジョブを送信する直前、トランスパイラが最適化した物理回路図を確認することがあります。この図は元の回路より複雑ですが、実機でのノイズやエラーの原因を究明する手がかりになります。 |
| 結果の解釈 | 実機から返された結果(例: ヒストグラム)が理論と異なるとき、どのゲートがどの量子ビットに影響を与えたかを回路図に立ち返って確認します。例えば、CNOTゲートが原因で特定のノイズが発生したかを分析する際に使用します。 |
| 誤り軽減の可視化 | 次回予定のノイズ軽減のプロセスで、補正後の結果が、設計した論理回路図の理想的な結果にどれだけ近づいたかを判断するために、回路図の論理が基準として使われます。 |
第3章:量子プログラミングの「単語帳」:主要な単一量子ビットゲート
前回登場した Hゲートに加え、最も頻繁に利用される基本的な量子ゲートを紹介します。
これらはすべて、1つの量子ビットの状態を操作します。
従来のプログラミング言語(JavaやPythonなど)でたとえるならば、メソッドのようなものと言えるかもしれません。
入門編の本記事では、以下に挙げる5種類をしっかり理解・記憶しておければ問題ありません。
| ゲート/記号 | 役割 | アナロジー(比喩) | Qiskitコード |
|---|---|---|---|
| Hゲート/H | 重ね合わせを作る(初期状態の|0⟩を、0 と 1 が半々の重ね合わせ状態にする)。 | コインを空中に投げ、回転させる。 | circuit.h(q_idx) |
| Xゲート/X または NOT | ビット反転を行う(|0⟩を |1⟩ に、|1⟩ を|0⟩ にする)。 | コインを裏返す。 | circuit.x(q_idx) |
| Iゲート/I | 何もしない(Identity、恒等操作)。デバッグなどで使用。 | 何も操作しない。 | circuit.i(q_idx) |
| Zゲート/Z | 位相反転(|1⟩の状態の「位相」を反転させる)。(※1) | コインの裏側(1の状態)に印をつける。 | circuit.z(q_idx) |
| CNOTゲート/CX | 制御ビットの状態に応じて、標的ビットを反転させる。(第5章で後述) | 完全に連動する2枚のコイン。 | circuit.cx(qc_idx, qt_idx) |
※1:「位相」、「位相反転」とは
「位相」という用語は、数学や物理学で広く使われますが、量子プログラミングで重要なのは、「波のズレ」というイメージです。
二つの波を重ね合わせたときに、タイミングが揃っていれば波は強まり、タイミングがズレていれば波は打ち消し合います。
量子プログラミングでは、この「波のズレ(位相)」を Z ゲートで操作することで、意図的に計算結果を強めたり(正解の確率を高める)、打ち消したり(不正解の確率を消す)します。
「位相反転」とは量子状態の「位相」と呼ばれる内部的な性質を変化させる操作です。
これは、たとえるなら、「|1⟩ 状態にだけ、誰にも見えない『特殊なラベル』を貼る」操作に似ています。
測定結果の確率自体は変わりませんが、このラベルが将来の計算で劇的な効果を生み出すのです。
第4章:実践:単一ゲートを使った回路の作成
この章では、XゲートとHゲートを組み合わせた回路を作成し、その動作をシミュレーターで確認します。(実機には接続しません)
① 事前準備
回路図を描画するために、Qiskitが依存している外部ライブラリを追加する必要があります。
VS Codeのターミナル内で、以下のコマンドを打ち込み、実行してください。
pip install pylatexenc② サンプルプログラムの作成と実行
新しいPythonファイル(例: single_gates.py)を作成し、以下のコードを記述してください。
single_gates.pyfrom qiskit.circuit import QuantumCircuit
from qiskit_aer.primitives import Sampler
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt
# 1量子ビット、1古典ビットの回路を作成
circuit = QuantumCircuit(1, 1)
# ① Xゲートの適用:初期状態 |0⟩ を |1⟩ に反転させる
# 引数の「0」はインデックス
circuit.x(0)
# ② Hゲートの適用:重ね合わせ状態にする
# 引数の「0」はインデックス
circuit.h(0)
# ③ 測定:結果を取り出す
# 引数は2つともインデックス
circuit.measure(0, 0)
# ----------------------------------
# 確率分布の計算と結果の取得 (Samplerの実行)
# ----------------------------------
# Samplerクラスのインスタンスを作成(ローカルシミュレーターを準備)
sampler = Sampler()
# 作成した回路をシミュレーターで実行し、結果をジョブとして取得(1000回測定)
job = sampler.run(circuit, shots=1000)
# ジョブが完了するのを待ち、最終的な測定結果オブジェクトを取得
result = job.result()
# 結果オブジェクトから、最初の回路の測定確率分布(counts)を取り出す
counts = result.quasi_dists[0]
# ----------------------------------
# 実行結果のコンソール出力
# ----------------------------------
# 測定結果の分布(例: {0: 0.509, 1: 0.491})をコンソールに出力
print("\n--- 測定結果 ---")
print(f"結果の分布(確率): {counts}")
# ----------------------------------
# 回路図の描画(図の作成)
# ----------------------------------
# 作成した量子回路を視覚化します
# 'mpl'を指定することで、matplotlibの描画形式で表示されます
circuit.draw("mpl")
# グラフ(回路図)を画面に表示します
# 回路図の画面を閉じると次のヒストグラムが表示されます
plt.show()
# ----------------------------------
# 確率分布の可視化
# ----------------------------------
# 取得した確率分布(counts)を基にヒストグラム(棒グラフ)を作成
plot_histogram(counts)
# 作成したグラフを画面に表示し、閉じるまで維持する
plt.show()
# 警告を抑えるため、明示的にすべての図を閉じる
# これにより、プログラム終了前にグラフィックリソースを解放します
plt.close('all')③ 実行結果の解釈
上記のコードを実行すると、まずVS Codeのコンソールに結果が表示されます。
結果の分布は{0:∼0.5,1:∼0.5}となり、前回記事の結果と同じように約50%ずつになるはずです。
- Xゲートで |0⟩→~|1⟩ に変換されました。
- Hゲートは、その |1⟩ の状態に適用され、|0⟩ と |1⟩ の逆位相の重ね合わせを作った後、測定により 50/50 の確率で 0 または 1 が出ます。
次に、「量子回路図」が描画されます。
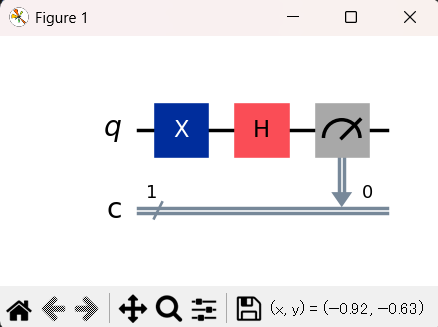
回路図では、量子ビットの線(qのライン)上に、X→H の順番でゲートが並んでいます。
これは、まず|0⟩ 状態を |1⟩ に反転させ(Xゲート)、その|1⟩ 状態に重ね合わせを適用(Hゲート)しているという、コードの意図が完全に回路図に反映されていることを示しています。
「c」の二重線は「古典ビット」で、測定結果の保管庫です。
量子回路図を閉じると、確率分布を視覚的に表すヒストグラムが表示されます。
これは、コンソール結果に表示された分布を視覚的に確認するためのツールです。
VS Codeのコンソールに表示されている確率分布と同じになっていることを確認してください。

第5章:複数量子ビット回路の読み方 ~CNOTゲートが示す条件付き論理
ここまでの回路はすべて1つの量子ビットで作成してきましたが、真の量子計算は複数の量子ビットを使って行われます。
- 回路図での表現: 量子ビットの線が2本、3本と増えます。
- Qiskitでの定義:
circuit = QuantumCircuit(2, 2)のように、引数を増やして定義します。
本章では、その連携の核となる複数量子ビットゲートの代表格、CNOTゲート(Controlled-NOT gate, CXゲート)の回路図と、それが示す条件付き論理を深く読み解くことで、回路図の読解力を飛躍的に向上させます。
単一ゲートの知識があれば、CNOTゲートの動作を理解するのは難しくありません。さっそく、2量子ビット回路の文法を学びましょう。
① CNOTゲートを含む回路の作成と描画
まずは、CNOTゲートを体験的に理解するために、2つの量子ビットを使った最もシンプルな回路を定義し、その図を視覚的に確認できるプログラムを作成しましょう。
VS Codeで新規のPythonファイル(例: cnot_intro.py)を作成し、以下のコードを記述して実行してください。
cnot_intro.pyfrom qiskit.circuit import QuantumCircuit
import matplotlib.pyplot as plt
# 2量子ビット(q0, q1)、2古典ビット(c0, c1)の回路を作成
# 複数量子ビット回路は、引数の数で定義します。
circuit = QuantumCircuit(2, 2)
# ----------------------------------
# CNOTゲートの適用
# ----------------------------------
# q0 を制御ビット(最初の引数)、q1 をターゲットビット(2番目の引数)として設定
circuit.cx(0, 1)
# ----------------------------------
# 測定(回路図を完全にするため)
# ----------------------------------
# q0, q1 の結果を c0, c1 に格納するよう定義
circuit.measure([0, 1], [0, 1])
# ----------------------------------
# 回路図の描画
# ----------------------------------
# 作成した量子回路を視覚化します
circuit.draw("mpl")
# グラフ(回路図)を画面に表示します
plt.show()
# 描画が終わったら図を閉じる
plt.close('all')上記のコードを実行すると、以下のようなCNOTゲートを含む量子回路図が描画されます。
(今回はコンソールに結果を表示させていません)
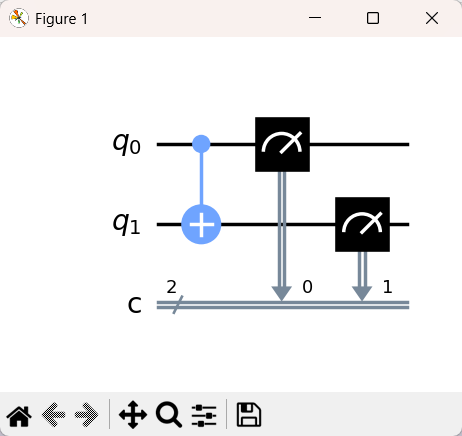
この回路図の読み方が、複数量子ビット回路を理解する鍵となります。
次セクションで、このCNOTゲートの構造を読み解きましょう。
② CNOTゲートの構成とルール:量子的な「IF-THEN」論理
②-1. 回路図における \(q_0\) と \(q_1\) の意味
\(q_0, q_1\) のラインは、量子ビットのインデックスを表します。
回路図の左側に \(q_0, q_1, q_2, \ldots\) と連番が振られ、それぞれの横線が独立した量子ビットを表します。
- \(q_0\) のライン:1番目の量子ビット(インデックス0)
- \(q_1\) のライン:2番目の量子ビット(インデックス1)
②-2. 回路図上のCXゲート(Controlled-NOT gate)
- \(q_0\) 上の青丸(●):CX(CNOT)ゲートの「制御量子ビット」
- このビットの状態が \(\vert 1\rangle\) であるか否かをチェックします。
- プログラムコードでは、
circuit.cx(0, 1)の最初の引数(0)に対応しています。
- \(q_1\) 上のプラス(⊕):CX(CNOT)ゲートの「ターゲット量子ビット」
- 「実行」される操作を受ける対象(ターゲット)となる量子ビットです。
- プログラムコードでは、
circuit.cx(0, 1)の2番目の引数(1)に対応しています。
③-3. 回路図全体の分析
セクション①で描画した図には、2つの量子ビットの状態を関連づけるための重要なゲートであるCNOTゲート(Controlled-NOT gate/CXゲート)が含まれています。
このゲートが、真の量子計算や、後の記事で扱う量子もつれの核心を担っています。
CNOTゲートの回路図は、2つの異なる記号で構成されています。
この構造は、古典的なプログラミングにおける「もし〜ならば、〜せよ(IF-THEN)」という条件付きの論理操作を表していると読み解きます。
CNOTゲートが示すルールは非常に明確です。
「制御ビットの状態が \(\vert 1\rangle\) ならば、ターゲットビットの状態を反転せよ(NOT操作を適用せよ)」
この条件付き操作の結果を、数学的な知識なしに理解するために、古典的な論理回路で使う真理値表を使って、4つの入力パターンすべてを読み解いてみましょう。
| 入力状態 |q1 q0⟩ | 制御ビット (q0)の値 | ターゲットq1 の操作 | 出力状態 |q1 q0⟩ | 読み方 |
|---|---|---|---|---|
| |00⟩ | 0 | 変化なし | |00⟩ | q0が0なので、何もしない。 |
| |01⟩ | 1 | 反転(0 → 1) | |11⟩ | q0が1なので、q1をXゲートで反転させる。 |
| |10⟩ | 0 | 変化なし | |10⟩ | q0が0なので、何もしない。 |
| |11⟩ | 1 | 反転(1 → 0) | |01⟩ | q0が1なので、q1をXゲートで反転させる。 |
⚠️ 注意:状態表記の順番について
今回の真理値表や、Qiskitの結果(例:\(\vert 11\rangle\), \(\vert 01\rangle\))では、状態の表記が\(|q_1 q_0\rangle\)の順になっています。
これは、回路図の物理的な線の順番(\(q_0\) が上、\(q_1\) が下)と異なり、インデックスの低いビット(\(q_0\))を右側(最下位ビット)に書くという量子コンピューティングの一般的な慣例に従っているためです。
したがって、真理値表を読む際は、「状態 \(|q_1 q_0\rangle\) の右端(後に書かれている方)が \(q_0\) の値、左端(先に書かれている方)が \(q_1\) の値」であることを念頭に置いてください。
この表を理解することで、複雑に見える複数量子ビットの回路図も、「いつ、どのビットが反転するか」という論理の連鎖として読み解けるようになります。
まとめ
今回の記事では、量子プログラミングの「言語」を構成する最も基本的な要素を学び、知識を飛躍的に向上させることができたのではないでしょうか。
今回達成したことリストで習得度を確認しましょう。
- 今回達成したことリスト
- 量子ゲートの操作:H、X、I、Z という単一量子ビットゲートの役割と、それが量子ビットに何をもたらすかをアナロジー(比喩)を通して直感的に理解しました。
- 単一量子ゲート操作の実践:X ゲートと H ゲートを組み合わせた回路をコードで記述し、シミュレーターで実行することで、意図した通りの重ね合わせの状態が作られることを確認しました。
- 回路図の読み方(入門編):単一ゲートの順番に加え、複数量子ビット回路の核となるCNOTゲート(CXゲート)の回路図が、どのように描かれ、何を意味するのかを理解しました。
- CNOTの論理構造:CNOTゲートのルール「制御ビットが \(\vert 1\rangle\) ならば、ターゲットビットを反転させる」という条件付き論理を、真理値表を通じて習得しました。
- 量子プログラミングの基礎固め:複数量子ビットゲートの基本構造を理解することで、今後の量子アルゴリズムの理解に向けた強固な基礎を確立しました。
- 次へのステップ:不確実性を解き明かす
- あなたは今、単なるコードの実行者ではなく、量子ビットを意図通りに操作できる量子プログラマーになりました。
- しかし、量子プログラミングには、まだ「測定の不確実性」という大きな疑問が残っています。なぜ、重ね合わせの状態を測ると結果がランダムに50%ずつに分かれるのでしょうか。
次回の第3回記事では、この「不確実性」に真正面から向き合います。
具体的には、量子測定の仕組みを深く理解し、ローカルシミュレーターに意図的にノイズを導入するコードを書き、実機で結果がブレる仕組みを体験的に解明します。



コメント