これまでの記事を通じて、量子プログラミングの基礎を完璧に固めてきました。
X、Hゲートでの状態操作、そして測定のランダムな仕組みや、実機に不可欠なノイズの現実を体験しました。
私たちは既に、「量子の海」を泳げる状態にあります。
とは言え、単一の量子ビットだけでは、従来のコンピュータを超えることはできません。
量子コンピュータが真に強力な力を発揮するのは、複数の量子ビットが連携し合ったときです。
そこで今回のテーマは、かのアルベルト・アインシュタインが「不気味な遠隔作用(spooky action at a distance)」と呼んで嫌悪した、量子の究極の現象、「量子もつれ(Entanglement)」です。
「量子もつれ」とは、二つの量子ビットが距離に関係なく、切っても切れない強い相関を持つ状態のことです。
片方を測定すると、瞬時にもう片方の状態が決まります。
本記事では、この「もつれ」を実現するための鍵となるCNOT (制御NOT) ゲートの使い方をマスターし、量子コンピュータの歴史で最も有名で基本的なもつれ状態である「ベル状態」をコーディングすることで、その驚くべき結果を観察します。
目次
第1章:CNOTゲートの仕組みと役割
これまでのHやXゲートの操作対象が単一の量子ビットだったのに対し、量子もつれは2つ以上の量子ビット間の関係です。
この関係を作り出す鍵となるのが、制御NOT(Controlled-NOT)ゲート、略して「CNOTゲート」です。
①CNOTゲートとは何か
CNOT ゲートは、次の2つの量子ビットを使います。
- 制御(Control)量子ビット:
- CNOT の操作を「実行するか、しないか」を決める量子ビット。
- 標的(Target)量子ビット:
- 実際に NOT 操作(ビット反転)を受ける量子ビット。
CNOT ゲートのルールは非常に単純です。
CNOTゲートのルール:
制御量子ビットが |1⟩ の状態のときのみ、標的量子ビットにXゲート(NOT操作)を適用する。
②量子回路図での表現
CNOTゲートは、量子回路図では以下のような独自のアイコンで表現されます。
- 上の線(制御): 小さな黒丸(下図の画像では青丸)で示されます。この量子ビットの状態が 1 のとき、操作が有効になります。
- 下の線(標的): 円と十字(⊕)で示されます。この量子ビットが NOT 操作を受けます。
③CNOTの動作を古典的な真理値表で確認
CNOTゲートの制御の仕組みを明確にするため、動作を古典的な入出力表(真理値表)で確認してみましょう。
| 制御ビット | 標的ビット | NOT操作有無 | 標的の出力 |
|---|---|---|---|
| 0 | 0 | 無 | 0 |
| 0 | 1 | 無 | 1 |
| 1 | 0 | 有 | 1 |
| 1 | 1 | 有 | 0 |
重要なのは、制御ビットが 1 の行だけ、標的ビットが反転している点です。
④CNOTが「量子もつれ」を生む理由
古典的なCNOT(制御NOT)はただのロジックゲートですが、量子コンピュータでは特別な役割を果たします。
- 重ね合わせの制御:
- Hゲートなどによって、制御量子ビットが|0⟩ と |1⟩ の重ね合わせになっている状態でCNOTを適用すると、|0⟩ のロジックと |1⟩ のロジックが同時に標的量子ビットに適用されます。
- 結果:
- 2つの量子ビットはもはや分離できなくなり、運命共同体となります。これが次章で実際にプログラミングして体験する「量子もつれ」の原理的な始まりです。
第2章:【実践】ベル状態のコーディング
量子もつれの状態のうち、最もシンプルで有名なものが「ベル状態(Bell State)」です。
ベル状態は、2つの量子ビットが最大限にもつれた、運命共同体の状態を指します。
この状態を作り出すための回路は、「Hゲート」と「CNOTゲート」を一つずつ組み合わせるだけで完成します。
①ベル状態回路を構築するプログラム
まず、2つの量子ビットと2つの古典ビットを持つ回路を定義します。
from qiskit.circuit import QuantumCircuit
# ----------------------------------
# 1. 回路の定義 (H + CNOT)
# ----------------------------------
# 2つの量子ビット(q[0], q[1])、2つの古典ビット(c[0], c[1])を作成
circuit = QuantumCircuit(2, 2)
# Hゲートの適用:インデックス0の量子ビット(q[0])を重ね合わせにする
circuit.h(0)
# CNOTゲートの適用:もつれを生成
# cxはCNOTゲートを意味するQiskitの命令
# 引数1:制御ビット(q[0])のインデックス
# 引数2:標的ビット(q[1])のインデックス
circuit.cx(0, 1)
# 測定:結果を取り出す
# q[0]をc[0]へ、q[1]をc[1]へ測定
circuit.measure([0, 1], [0, 1])②コードの解説
QuantumCircuit(2, 2):これまで 1 Qubit だったものが、初めて 2 Qubit の回路になりました。circuit.h(0):最初の量子ビット (q[0]) が |0⟩ と |1⟩ の重ね合わせ状態になります。circuit.cx(0, 1):ここが核心です。重ね合わせの状態にある q[0] を制御ビットとして、q[1] に CNOTゲートを適用します。circuit.measure([0, 1], [0, 1]):2つの量子ビットを、2つの古典ビットにそれぞれ測定し、結果を取り出します。
③実行と結果を可視化するプログラム
まずは、以下の通りインポート文を追加する必要があります。
from qiskit.circuit import QuantumCircuit
# 以下の3つを追加してください
from qiskit_aer.primitives import Sampler
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt続いて、①で作成した回路を実行し、結果をヒストグラムで確認するためのプログラムコードです。
今回は、ノイズのない理想的な Sampler を使用します。
※ circuit.measure([0, 1], [0, 1]) の続きとしてコーディングしてください。
# ----------------------------------
# 実行と可視化
# ----------------------------------
# Samplerクラスのインスタンスを作成(ローカルシミュレーターを準備)
sampler = Sampler()
# 回路図の描画
circuit.draw("mpl")
plt.show()
# 作成した回路をシミュレーターで実行(1000回測定)
job = sampler.run(circuit, shots=1000)
result = job.result()
# 結果の分布(counts)を取り出す
counts = result.quasi_dists[0]
# 測定結果の分布をコンソールに出力
print("\n--- ベル状態の測定結果 ---")
print(f"結果の分布(確率): {counts}")
# 取得した確率分布(counts)を基にヒストグラムを作成
plot_histogram(counts)④プログラムコードの全文掲載
from qiskit.circuit import QuantumCircuit
from qiskit_aer.primitives import Sampler
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt
# ----------------------------------
# 1. 回路の定義 (H + CNOT)
# ----------------------------------
# 2つの量子ビット(q[0], q[1])、2つの古典ビット(c[0], c[1])を作成
circuit = QuantumCircuit(2, 2)
# Hゲートの適用:インデックス0の量子ビット(q[0])を重ね合わせにする
circuit.h(0)
# CNOTゲートの適用:もつれを生成
# cxはCNOTゲートを意味するQiskitの命令
# 引数1:制御ビット(q[0])のインデックス
# 引数2:標的ビット(q[1])のインデックス
circuit.cx(0, 1)
# 測定:結果を取り出す
# q[0]をc[0]へ、q[1]をc[1]へ測定
circuit.measure([0, 1], [0, 1])
# ----------------------------------
# 実行と可視化
# ----------------------------------
# Samplerクラスのインスタンスを作成(ローカルシミュレーターを準備)
sampler = Sampler()
# 回路図の描画
circuit.draw("mpl")
plt.show()
# 作成した回路をシミュレーターで実行(1000回測定)
job = sampler.run(circuit, shots=1000)
result = job.result()
# 結果の分布(counts)を取り出す
counts = result.quasi_dists[0]
# 測定結果の分布をコンソールに出力
print("\n--- ベル状態の測定結果 ---")
print(f"結果の分布(確率): {counts}")
# 取得した確率分布(counts)を基にヒストグラムを作成
plot_histogram(counts)
plt.show()
# 終了時の警告抑制
plt.close("all")
実行結果は、次章(第3章)で詳しく解釈しますが、コンソールの結果(counts)とヒストグラムに注目してください。
特定のパターンの結果しか出ていないことに気づくはずです。
第3章:結果の解釈
コードを実行すると、最初に回路図が表示されるはずです。
回路図を閉じると、コンソール出力とヒストグラムが表示されます。
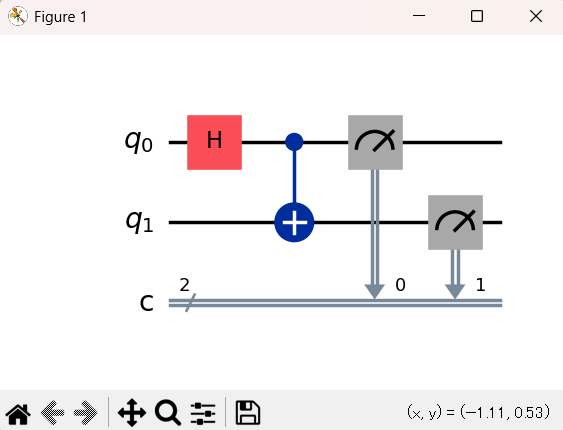
①回路図の解釈

👆の回路図は、コードの意図通りに量子もつれの状態を作り出す「ベル状態」の回路を正確に表しています。
| 要素 | 対応するコード | 役割 |
|---|---|---|
| q₀ の Hゲート | circuit.h(0) | q₀ を |0⟩ と |1⟩ の重ね合わせ状態にします。 |
| q₀ の黒(青)丸 :制御 | circuit.cx(0, 1) | q₀ が 1 のとき、操作を実行する制御ビットです。 |
| q₁ の ⊕ :標的 | circuit.cx(0, 1) | q₁ が NOT操作を受ける標的ビットです。 |
| 2つのメーター | circuit.measure([0, 1], [0, 1]) | q₀ と q₁ の状態を測定し、下の古典ビット c に結果を記録します。 |
②コンソールとヒストグラムでの測定結果の確認
--- ベル状態の測定結果 ---
結果の分布(確率): {3: 0.506, 0: 0.494}コンソール結果には3(二進数で11)と0(二進数で00)の確率分布が表示されています。
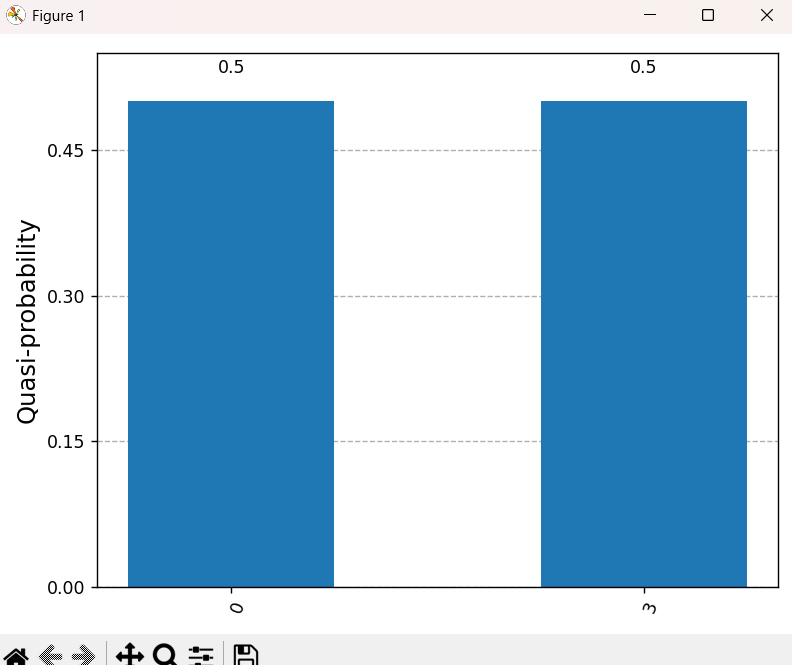
ヒストグラムにも、0(00) と 3(11) の2つの棒グラフしか表示されず、その他の 1(01) や 2(10) の結果はほぼゼロになったはずです。
- 0(
00): 最初の量子ビット (q1) と 2番目の量子ビット (q0) の両方が 0 の状態。 - 3(
11): 両方の量子ビットが 1 の状態。
③「もつれ」の正体は「強い相関」
この結果が量子もつれの決定的な証拠であると言えます。
- ランダムであること:Hゲートの影響で、結果が 00 になるか 11 になるかは50/50 の確率でランダムです。
- 相関が完璧であること:結果が 0 になると決まった場合、もう片方も必ず 0 になります。逆に 1 になると決まった場合、もう片方も必ず 1 になります。
現実の世界、そして古典的なシステムでは、2枚の独立したコインを1000回投げて表と裏が必ず一致するようなことは起こりえません。
これが、「切っても切れない強い相関」を持つ「量子もつれ」の力なのです。
ではなぜ、H と CNOT の組み合わせでこのような状態が生まれたのでしょうか。
- H ゲート:最初のq0を「|0⟩のロジック」と「|1⟩ のロジック」が混ざった重ね合わせにします。
- CNOT ゲート:
- q0 が |0⟩ のロジックを実行するとき → q1 は何もしない → |00⟩ の状態が生まれる。
- q0 が |1⟩ のロジックを実行するとき → q1 はNOT操作で反転する👉 |11⟩の状態が生まれる。
結果として、回路は |00⟩ と |11⟩ の重ね合わせ(ベル状態)となり、もつれが完成しました。
アインシュタインはこの完璧な相関関係に非常に驚き、生涯を通じてこの現象を否定し、反証しようと試み続けました。
量子ビットがどれだけ離れていても、片方の状態が確定すると、瞬時にもう片方の状態も確定するという事実は、「局所的実在論」(物理現象は近くで起きる)という彼の信念に反していたためです。
まとめ
今回は、複数量子ビットの世界に足を踏み入れ、量子もつれという、古典物理学の常識を覆す現象をプログラムで実現しました。
- CNOTゲートの習得:CNOT ゲートが、制御ビットが |1⟩ のときのみ標的ビットを反転させるという、制御ロジックを持っていることを学びました。
- ベル状態の生成: Hゲートと CNOTゲートを組み合わせることで、|00⟩ と |11⟩ の結果しか出ないという、完璧な相関を持つベル状態を生成し、量子もつれを体験しました。
この「もつれ」こそが、量子コンピュータが古典コンピュータに対して圧倒的な優位性(量子優位性)を発揮する根本的な力です。
アインシュタインが驚いたこの現象を、私たちは今、自分で記述するコードで制御できるようになったのです。



コメント