前回の「平方完成」までで、代数計算の重要スキルをマスターしました。
これらは言わば、建築の土台を作る作業でした。
今回からは、いよいよ「波」を扱うための数学へと進んでいきます。
この数学の旅で最初に出会うのが、「三角比(さんかくひ)」です。
「三角比は苦手」と感じる方もいるかもしれませんが、心配はいりません。三角比の核心は、直角三角形の中にある二辺の長さの比を計算することに尽きます。
これは、複雑な計算というよりも、定義を覚えることが9割です。
この記事では、まず\(\sin, \cos, \tan\) のそれぞれの定義を徹底的に習得します。
そして、三角比の間で成り立つ最重要公式「ピタゴラスの定理(三平方の定理)」の応用を、その意味とともに理解します。
三角比の基礎が不安定なまま、次の「三角関数(波)」に進むのは危険です。
この単元で、確固たる計算スキルを身につけ、次のステップへ進むための準備を万全にしましょう。
目次
第1章:サイン(sign)、コサイン(cosine)、タンジェント(tangent)の正体
① 三角比の定義
三角比とは、直角三角形の鋭角 (\(\theta\)) に対して、2辺の長さの比を定めたものです。
角度 (\(\theta\)) が決まれば、三角形の大きさにかかわらず、この比率は常に一定になる、というのが最も重要なポイントです。
①-1. 直角三角形と3つの基本比
直角三角形において、角度 \(\theta\) に対応する3つの基本比は、以下の通り定義されます。
| 名称 | 英単語 | 定義 (比) | 役割 |
|---|---|---|---|
| サイン (\(\sin \theta\)) | Sign | \(\displaystyle \frac{\text{対辺(高さ)}}{\text{斜辺}}\) | 斜辺に対する縦の割合を決定 |
| コサイン (\(\cos \theta\)) | Cosine | \(\displaystyle \frac{\text{隣辺(底辺)}}{\text{斜辺}}\) | 斜辺に対する横の割合を決定 |
| タンジェント (\(\tan \theta\)) | Tangent | \(\displaystyle \frac{\text{対辺(高さ)}}{\text{隣辺(底辺)}}\) | 横に対する縦の割合(傾き)を決定 |
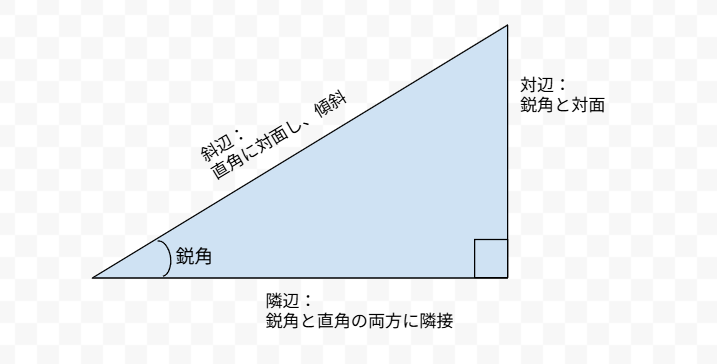
これらの定義を覚えるコツは、各辺が「鋭角と対面している(=対辺)」、「鋭角と直角の両方に隣接している(=隣辺)」、「直角と対面し傾斜している(=斜辺)」をしっかり区別することです。
①-2. 最重要公式:相互関係を理解する
三角比の間で成り立つ、後の計算に不可欠な最重要公式を2つ確認します。
- 相互関係 I:ピタゴラスの定理の別表現
\(\sin \theta\) と \(\cos \theta\) の間には、ピタゴラスの定理(三平方の定理)から導かれる、以下の関係が成り立ちます。- \(\mathbf{\sin^2 \theta + \cos^2 \theta = 1}\)
- 相互関係 II:タンジェントの定義
タンジェントは、サインとコサインの比としても表現できます。- \(\mathbf{\tan \theta = \displaystyle\frac{\sin \theta}{\cos \theta}}\)
相互関係 I の公式は、「縦(対辺)の長さの二乗 (\(\sin^2 \theta\)) と横(隣辺)の長さの二乗 (\(\cos^2 \theta\)) の和が斜辺の二乗 (\(\mathbf{1^2=1}\)) になる」という、三平方の定理そのものを意味しています。
相互関係 II の公式は、「傾き」である \(\tan \theta\) が、「対辺の長さ」を「隣辺の長さ」で割った値(変化の割合)である、という幾何学的な意味と一致します。
三平方の定理とは:
三平方の定理は、「ピタゴラスの定理」とも呼ばれ、直角三角形の直角を挟む2辺を(\(a, b\))、斜辺(最も長い辺)を(\(c\))とする3辺の長さ(\(a, b, c\))の間にある関係を示した定理で、「\(a^2 + b^2 = c^2\)」と表されます。
この公式は、次の計算に応用されます。
- 2辺の長さが分かれば残りの1辺の長さを計算できる
- 2点間の距離の計算や、対象の三角形が直角三角形かどうかを判定できる
② 特殊角の三角比
三角比の計算で特に頻繁に使う角、すなわち \(\mathbf{30^\circ}\)、 \(\mathbf{45^\circ}\)、 \(\mathbf{60^\circ}\) は、特殊角(とくしゅかく)と呼ばれます。
💡 特殊角とは
特殊角とは、三角比(三角関数)の値が、\(\mathbf{\sqrt{}}\) を使った分数(無理数)や整数で正確に表せる角度のことです。
特殊角は、辺の長さの比が常にシンプルな整数や \(\mathbf{\sqrt{}}\) を含む決まった組み合わせになるという特性を持っています。
この特性により、これらの角の三角比の値は例外的に正確に求めることができ、特別な直角三角形(正三角形を半分にしたもの、または直角二等辺三角形)から導かれます。
②-1. 必須の基本角の三角比
| 角度 (\(\theta\)) | \(\sin \theta\) (対辺/斜辺) | \(\cos \theta\) (隣辺/斜辺) | \(\tan \theta\) (対辺/隣辺) |
|---|---|---|---|
| \(30^\circ\) | \(\displaystyle {\frac{1}{2}}\) | \(\displaystyle {\frac{\sqrt{3}}{2}}\) | \(\displaystyle {\frac{1}{\sqrt{3}}}\) |
| \(45^\circ\) | \(\displaystyle {\frac{1}{\sqrt{2}}}\) | \(\displaystyle {\frac{1}{\sqrt{2}}}\) | \(\mathbf{1}\) |
| \(60^\circ\) | \(\displaystyle {\frac{\sqrt{3}}{2}}\) | \(\displaystyle {\frac{1}{2}}\) | \(\mathbf{\sqrt{3}}\) |
これらの値は暗記するに越したことはないのですが、以下の辺の比を頭に入れておけばいつでも導出できます。
- \(45^\circ\) の直角三角形: 辺の比は \(1 : 1 : \sqrt{2}\) (直角二等辺三角形)
- \(30^\circ, 60^\circ\) の直角三角形: 辺の比は \(1 : \sqrt{3} : 2\) (正三角形を半分にしたもの)
💡丸暗記を不要にする「2つの魔法の三角形」
上記の表のすべての値は、次の2つの特別な直角三角形を覚えておくことで、簡単に導き出すことができます。
1つ目は、\(45^\circ\) の三角形:辺の比は \(1:1:\sqrt{2}\)
これは直角二等辺三角形ですね。
覚える辺の比 \(1 : 1 : \sqrt{2}\)は、それぞれ(隣辺 : 対辺 : 斜辺)に対応します。
導出は以下の通りです。
- \(\displaystyle \sin 45^\circ = \frac{\text{対辺}}{\text{斜辺}} = \frac{1}{\sqrt{2}}\)
- \(\displaystyle \cos 45^\circ = \frac{\text{隣辺}}{\text{斜辺}} = \frac{1}{\sqrt{2}}\)
- \(\displaystyle \tan 45^\circ = \frac{\text{対辺}}{\text{隣辺}} = \frac{1}{1} = 1\)
2つ目は、\(30^\circ\) と \(60^\circ\) の三角形:辺の比は \(1:\sqrt{3}:2\)
これは正三角形を半分にしたものですね。
ここでは、対辺と隣辺を明確に定義するため、正三角形を縦に半分にしたものとして考えます。
覚える辺の比 \(1 : \sqrt{3} : 2\)は、それぞれ隣辺(=一番短い辺) : 対辺(=中間の辺) : 斜辺)に対応します。
導出は以下の通りです。
- \(\mathbf{30^\circ}\) の視点: 対辺 (縦)が \(1\)、隣辺 (横)が \(\sqrt{3}\)、斜辺が \(2\)
- \(\displaystyle \sin 30^\circ = \frac{\text{対辺}}{\text{斜辺}} = \frac{1}{2}\)
- \(\displaystyle \cos 30^\circ = \frac{\text{隣辺}}{\text{斜辺}} = \frac{\sqrt{3}}{2}\)
- \(\displaystyle \tan 30^\circ = \frac{\text{対辺}}{\text{隣辺}} = \frac{1}{\sqrt{3}}\)
- \(\mathbf{60^\circ}\) の視点: 対辺と隣辺が入れ替わるので、対辺 (縦)が \(\sqrt{3}\)、隣辺 (横)が \(1\)、斜辺が \(2\)
- \(\displaystyle \sin 60^\circ = \frac{\text{対辺}}{\text{斜辺}} = \frac{\sqrt{3}}{2}\)
- \(\displaystyle \cos 60^\circ = \frac{\text{隣辺}}{\text{斜辺}} = \frac{1}{2}\)
- \(\displaystyle \tan 60^\circ = \frac{\text{対辺}}{\text{隣辺}} = \frac{\sqrt{3}}{1} = \sqrt{3}\)
第1章の練習問題
【問題 1-1】 サインとコサインの計算
直角三角形において、\(\displaystyle \sin \theta = \frac{4}{5}\) であるとき、\(\cos \theta\) と \(\tan \theta\) の値を求めよ。
解答を見る
相互関係より、\(\cos^2 \theta = 1 – \sin^2 \theta\)
\(\displaystyle = 1 – \left(\frac{4}{5}\right)^2 = 1 – \frac{16}{25} = \frac{9}{25}\)
\(\theta\) は鋭角なので \(\cos \theta > 0\) より、\(\displaystyle \cos \theta = \mathbf{\frac{3}{5}}\)
\(\displaystyle \tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{4/5}{3/5} = \mathbf{\frac{4}{3}}\)
【問題 1-2】 タンジェントからの計算
ある直角三角形で、\(\displaystyle \tan \theta = \frac{1}{\sqrt{3}}\) のとき、\(\sin \theta\) と \(\cos \theta\) の値を求めよ。
解答を見る
縦 \(= 1\)、横 \(= \sqrt{3}\) のとき、
斜辺 \(c\) は \(c^2 = 1^2 + (\sqrt{3})^2\)
\( = 1 + 3 = 4\) より \(c = 2\) です。
三角比の定義より、
\(\displaystyle \sin \theta = \frac{\text{対辺(縦)}}{\text{斜辺}} = \mathbf{\frac{1}{2}}\)
\(\displaystyle \cos \theta = \frac{\text{隣辺(横)}}{\text{斜辺}} = \mathbf{\frac{\sqrt{3}}{2}}\)
【問題 1-3】 特殊角の計算(加法)
以下の計算結果を求めよ。
\(\sin 60^\circ + \cos 30^\circ\)
解答を見る
\(\sin 60^\circ = \frac{\sqrt{3}}{2}\)、\(\cos 30^\circ = \frac{\sqrt{3}}{2}\) なので、
\(\frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2} = \frac{2\sqrt{3}}{2} = \mathbf{\sqrt{3}}\)
【問題 1-4】 特殊角の計算(乗法)
以下の計算結果を求めよ。
\(\tan 45^\circ \times \sin 30^\circ\)
解答を見る
\(\tan 45^\circ = 1\)、\(\sin 30^\circ = \frac{1}{2}\) なので、
\(1 \times \frac{1}{2} = \mathbf{\frac{1}{2}}\)
【問題 1-5】 特殊角の計算(除法)
以下の計算結果を求めよ。
\(\displaystyle \frac{\cos 60^\circ}{\sin 45^\circ}\)
解答を見る
\(\cos 60^\circ = \frac{1}{2}\)、\(\sin 45^\circ = \frac{1}{\sqrt{2}}\) なので、
\(\frac{1/2}{1/\sqrt{2}} = \frac{1}{2} \times \sqrt{2} = \frac{\sqrt{2}}{2}\)
第2章:三角比の応用と関係式
① 角度の拡張: \(90^\circ – \theta\) の関係
第1章で学んだ三角比は、鋭角 (\(\mathbf{0^\circ < \theta < 90^\circ}\)) の直角三角形内でのみ定義されました。
このセクションでは、三角形の内角の和(\(180^\circ\))を利用して、異なる2つの鋭角の三角比の関係を探ります。
直角三角形の鋭角が \(\mathbf{0^\circ < \theta < 90^\circ}\) になるのには自明の理があります。
- 直角三角形の内角の和は \(\mathbf{180^\circ}\) です。
- そのうち、1つの角が必ず直角 (\(\mathbf{90^\circ}\)) です。
- 残りの2つの角は「鋭角」であり、\(\mathbf{90^\circ}\) 未満でなければなりません。
故に、もしも角度が \(90^\circ\) 以上になると、その三角形は直角三角形ではなくなってしまいます(鈍角三角形など)。
この制限を解消し、\(\mathbf{90^\circ}\) を超える角度(鈍角、負の角、360°以上の角)を扱えるようにするのが、次回の記事で学ぶ「三角関数(単位円による拡張)」です。
①-1. \(\sin\) と \(\cos\) の入れ替わり
直角三角形において、直角(\(90^\circ\))を除いた残りの2つの鋭角を \(\theta\) と \(\mathbf{90^\circ – \theta}\) とします。
この2つの角を別の視点から見ると、「対辺」と「隣辺」の役割が、斜辺を軸にして互いに入れ替わります。
※ 下図のように三角形を回転させると考えるとイメージしやすいかと思います。
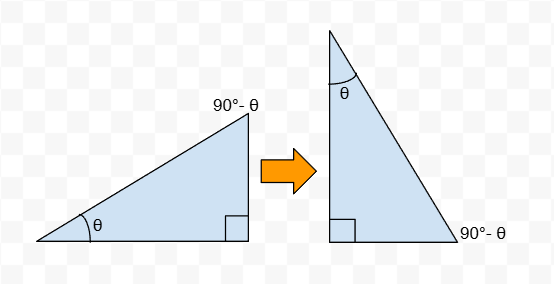
これが、以下の非常に重要な関係が成り立つ理由です。
- \(\sin \theta\) の値は、「\(\theta\) の対辺 / 斜辺」です。
- しかし、この \(\theta\) の対辺は、相方の \(\mathbf{90^\circ – \theta}\) から見ると、角を挟む「隣辺」になります。
したがって、\(\theta\) のサインと\(\mathbf{90^\circ – \theta}\) のコサインは、同じ辺の比 \(\displaystyle \left(\frac{\text{元の対辺}}{\text{斜辺}}\right)\) を使っているため、値が一致します。
\(\mathbf{\sin (90^\circ – \theta) = \cos \theta}\)
\(\mathbf{\cos (90^\circ – \theta) = \sin \theta}\)
これは、「ある角のサインの値は、その補角(\(\mathbf{90^\circ}\)になる相方)のコサインの値と等しい」ことを意味します。(例:\(\sin 30^\circ = \cos 60^\circ\))
①-2. タンジェントの関係
タンジェントも \(\sin\) と \(\cos\) の関係から、同様に \(90^\circ – \theta\) の関係式が導かれます。
タンジェントの定義は \(\mathbf{\tan \theta = \displaystyle\frac{\sin \theta}{\cos \theta}}\) でした (「第1章 ①-2. 最重要公式:相互関係を理解する」の公式2より)。
この関係に、先ほど導出した \(\sin (90^\circ – \theta)\) と \(\cos (90^\circ – \theta)\) の関係を代入します。
\(\tan (90^\circ – \theta) = \displaystyle\frac{\sin (90^\circ – \theta)}{\cos (90^\circ – \theta)}\)
右辺に \(\mathbf{\sin (90^\circ – \theta) = \cos \theta}\) と \(\mathbf{\cos (90^\circ – \theta) = \sin \theta}\) を代入すると、以下のようになります。
\(\tan (90^\circ – \theta) = \displaystyle\frac{\cos \theta}{\sin \theta}\)
これは、元の \(\tan \theta = \displaystyle\frac{\sin \theta}{\cos \theta}\) の分数全体が逆転した形になっています。したがって、タンジェントの関係は逆数になります。
\(\mathbf{\tan (90^\circ – \theta) = \displaystyle\frac{1}{\tan \theta}}\)
② 応用公式:その他の相互関係
第1章で、最重要公式として \(\mathbf{\sin^2 \theta + \cos^2 \theta = 1}\) を覚えました。
この公式は、すべての三角比の相互関係の土台となります。
このセクションでは、この土台から派生する他の重要な相互関係を、暗記せずに導出する方法を学びます。
②-1. \(1 + \tan^2 \theta\) の公式の導出
\(\sin \theta\) と \(\cos \theta\) の両方を含む公式 \(\sin^2 \theta + \cos^2 \theta = 1\) の両辺を \(\mathbf{\cos^2 \theta}\) で割ると、タンジェントを含む関係式が導かれます。
\(\sin^2 \theta + \cos^2 \theta = 1 \quad \text{の両辺を } \cos^2 \theta \text{ で割ると}\)👇
\(\displaystyle\frac{\sin^2 \theta}{\cos^2 \theta} + \displaystyle\frac{\cos^2 \theta}{\cos^2 \theta} = \displaystyle\frac{1}{\cos^2 \theta}\)
タンジェントの定義は \(\mathbf{\tan \theta = \displaystyle\frac{\sin \theta}{\cos \theta}}\) (「第1章 ①-2. 最重要公式:相互関係を理解する」の公式2より)であるため、以下の公式が得られます。
\(\mathbf{1 + \tan^2 \theta = \displaystyle\frac{1}{\cos^2 \theta}}\)
この公式は、「\(\tan \theta\) の値だけが分かっているときに、\(\cos \theta\) の値を求める」際に非常に有効です。
②-2. \(\sin^2 \theta\) を逆数で表す公式の導出
最重要公式 \(\sin^2 \theta + \cos^2 \theta = 1\) の両辺を今度は \(\mathbf{\sin^2 \theta}\) で割ると、もう一つの関係式が導出できます。(※この公式は、②-1の公式ほど頻繁には使いません。)
\(\sin^2 \theta + \cos^2 \theta = 1 \quad \text{の両辺を } \sin^2 \theta \text{ で割ると}\)👇
\(\displaystyle\frac{\sin^2 \theta}{\sin^2 \theta} + \displaystyle\frac{\cos^2 \theta}{\sin^2 \theta} = \displaystyle\frac{1}{\sin^2 \theta}\)
\(\frac{\cos \theta}{\sin \theta}\) は \(\tan \theta\) の逆数 (第2章 ①-2.「①-2. タンジェントの関係」より) であるため、以下の公式が得られます。
\(\mathbf{1 + \displaystyle\frac{1}{\tan^2 \theta} = \displaystyle\frac{1}{\sin^2 \theta}}\)
第2章の練習問題
【問題 2-1】 関係式の利用(加法)
以下の計算結果を求めよ。
\(\sin 10^\circ + \cos 80^\circ\)
解答を見る
\(\mathbf{80^\circ = 90^\circ – 10^\circ}\) なので、
\(\cos 80^\circ = \cos (90^\circ – 10^\circ) = \sin 10^\circ\) となり、
問題文の \(\cos 80^\circ\) は \(\sin 10^\circ\) とイコールになります。
ゆえに
\(\sin 10^\circ + \cos 80^\circ = \sin 10^\circ + \sin 10^\circ = \mathbf{2 \sin 10^\circ}\)
【問題 2-2】 関係式の利用(乗法)
以下の計算結果を求めよ。
\(\tan 20^\circ \times \tan 70^\circ\)
解答を見る
\(\mathbf{70^\circ = 90^\circ – 20^\circ}\) なので、
\(\tan 70^\circ = \displaystyle\frac{1}{\tan 20^\circ}\) です。
ゆえに
\(\tan 20^\circ \times \tan 70^\circ = \tan 20^\circ \times \displaystyle\frac{1}{\tan 20^\circ} = \mathbf{1}\)
【問題 2-3】 \(\tan\) から \(\cos\) の計算
\(\tan \theta = 3\) のとき、\(\cos \theta\) の値を求めなさい。
解答を見る
\(1 + \tan^2 \theta = \displaystyle\frac{1}{\cos^2 \theta}\) に
\(\tan \theta = 3\) を代入すると、
\(1 + 3^2 = 1 + 9 = 10\)
\(\displaystyle\frac{1}{\cos^2 \theta} = 10 \quad \to \quad \cos^2 \theta = \displaystyle\frac{1}{10}\)
\(\theta\) は鋭角なので \(\cos \theta > 0\) です。
\(\cos \theta = \displaystyle\frac{1}{\sqrt{10}} = \mathbf{\displaystyle\frac{\sqrt{10}}{10}}\)
【問題 2-4】 相互関係の証明
以下の等式が成り立つことを証明せよ。(ヒントの公式を使わずに、\(\sin \theta\) と \(\cos \theta\) を使って証明します。)
\(1 + \displaystyle\frac{1}{\tan^2 \theta} = \displaystyle\frac{1}{\sin^2 \theta}\)
解答を見る
\(\text{左辺} = 1 + \displaystyle\frac{1}{\tan^2 \theta} = 1 + \displaystyle\frac{\cos^2 \theta}{\sin^2 \theta}\)
\(\text{左辺} = \displaystyle\frac{\sin^2 \theta}{\sin^2 \theta} + \displaystyle\frac{\cos^2 \theta}{\sin^2 \theta} = \displaystyle\frac{\sin^2 \theta + \cos^2 \theta}{\sin^2 \theta}\)
ここで、分子に \(\mathbf{\sin^2 \theta + \cos^2 \theta = 1}\) を代入します。
\(\text{左辺} = \displaystyle\frac{1}{\sin^2 \theta} = \text{右辺}\)
よって、等式は成り立つ。
まとめ
以上で、三角比の基礎となる直角三角形の知識は、量子力学に必要な知識の土台としては万全かと思います。
以下の3つの重要ポイントが定着しているか確認しましょう。
| ポイント | 習得したスキル |
|---|---|
| 三角比の定義 | サイン (\(\sin\))、コサイン (\(\cos\))、タンジェント (\(\tan\)) の定義を、「斜辺」「対辺」「隣辺(底辺)」を使って正確に言える。 |
| 最重要公式 | \(\mathbf{\sin^2 \theta + \cos^2 \theta = 1}\) を暗記し、他の公式を導出できる。 |
| 拡張への準備 | \(90^\circ – \theta\) の関係を理解し、\(\sin\) と \(\cos\) が互いに入れ替わる理由を説明できる。 |
💡 次のステップへの繋がり
ここまでの知識は、角度が\(0^\circ\) から \(90^\circ\) の範囲でしか使えません。
しかし、量子力学で扱う「波の動き」や「回転」は、\(90^\circ\) を超える角度や、負の角度、360° を超える角度を扱います。
この制限を外し、三角比を実用的な関数「三角関数(Trigonometric Functions)」へと進化させるのが、次回のテーマです。



コメント