量子プログラミング【入門編】からコツコツと学習されてきた場合、もしかすると基本的なH(アダマール)ゲートやX(NOT)ゲートにはもう飽きた、という方もいらっしゃるかもしれません。
量子コンピュータの基本操作である「H」や「X」ゲートは、量子ビットの状態を離散的に(飛び飛びに)変化させます。
しかし、より量子状態を自在に操るためには、アナログ(連続的)な操作が不可欠です。
その鍵を握るのが、角度 \(\theta\) で状態を精密に回転させる回転ゲートです。
そこで今回からは、「回転ゲート三部作」として、ブロッホ球の三軸に対応する \(\text{R}_X, \text{R}_Y, \text{R}_Z\) の回転ゲートを、Qiskit & Python で使いこなす方法を解説します。
第1部となる本記事では、量子アルゴリズムの核心である位相操作を担う \(\text{R}_Z(\theta)\) ゲートに焦点を当て、その原理と量子的な干渉制御への応用を実践します。
第1章:量子回転ゲートとは何か
冒頭にもお伝えしたとおり、回転ゲート(Rotation Gate)は、「アナログ的な精密操作」を可能とします。
具体的には、状態を\(|0\rangle\)と\(|1\rangle\)の間に位置する任意の場所に精密に設定したり、わずかな位相のズレを導入することが可能です。
本章では、この回転ゲートが持つ役割と、量子計算における位置づけを確認します。
1.1. 回転ゲートが持つ「角度 \(\theta\)」
量子コンピュータの基本ゲートには、状態を反転させる\(\text{X}\)ゲートや、重ね合わせ状態を作り出す\(\text{H}\)ゲートのように、ゲートの作用が固定されているものが多く存在します。
しかし、実際の量子アルゴリズム、特に変分量子アルゴリズム(VQA)でのVQE手法などでは、最適化の過程で状態を微調整する必要があります。
この微調整を可能にするのが、角度パラメータ \(\theta\) を持つ回転ゲートです。
回転ゲートは、この \(\theta\) によって、量子ビットの状態ベクトルをブロッホ球上で任意の角度だけ回転させることを可能にします。
VQA と VQE
変分量子アルゴリズム (VQA: Variational Quantum Algorithm) は、量子コンピュータの計算能力と古典コンピュータの最適化能力を組み合わせて問題を解く手法の総称です。
VQE (Variational Quantum Eigensolver) は、この VQA のカテゴリの中で、特に分子の基底状態エネルギー(最も低いエネルギー)を求めることに特化したアルゴリズムです。
日本語では「変分量子固有値ソルバー」と呼ばれます。
1.1.1. 量子ビットをアナログ操作する
従来の古典コンピュータが情報を「0」か「1」という離散的(デジタル)な値で処理するのに対し、量子コンピュータは \(|0\rangle\) と \(|1\rangle\) の重ね合わせ状態を扱います。
この重ね合わせ状態を、任意の中間的な位置に設定したり、微調整したりする操作が「アナログ操作」です。
\(\text{R}_Z(\theta)\) などの回転ゲートは、このアナログ操作を実現する唯一の手段です。
これらのゲートはパラメータ \(\theta\)(角度)を持ち、その \(\theta\) の値を変えることで、量子状態をブロッホ球上で連続的に変化させることができます。
例えば、X ゲートは状態を \(180^\circ\) 回転させる操作として固定されていますが、回転ゲートを使えば \(45^\circ\) や \(90^\circ\)、あるいは \(1.23\) ラジアンといった任意の角度で状態を回転させ、極めて精密な量子状態を作り出すことが可能になります。
1.1.2. ブロッホ球の回転と\(R_Z\)の役割
回転ゲートが量子状態をアナログに操作する様子を視覚的に理解するためには、ブロッホ球 の概念が不可欠です。
ブロッホ球は、単一の量子ビットの状態を球の表面上の一点として表現する幾何学的なモデルです。
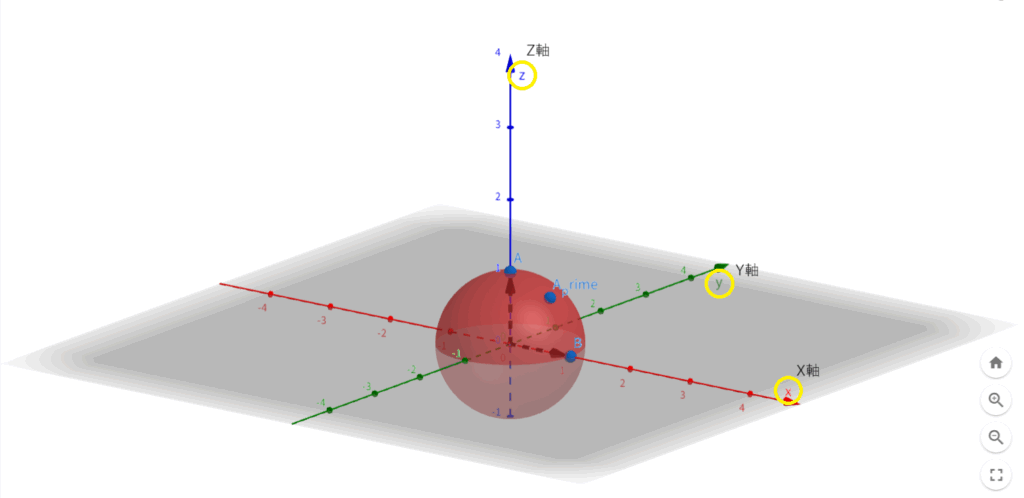
ブロッホ球には、上図に示したとおり、互いに直交する \(X\) 軸、 \(Y\) 軸、 \(Z\) 軸 の三つの軸が存在し、それぞれの軸を中心として量子状態を回転させるのが回転ゲートです。
| ゲート | 作用する回転軸 | 役割(効果) |
|---|---|---|
| \(\text{R}_X(\theta)\) | \(X\) 軸 | \(Y-Z\) 平面上の回転を制御。 |
| \(\text{R}_Y(\theta)\) | \(Y\) 軸 | \(X-Z\) 平面上の回転を制御。 |
| \(\text{R}_Z(\theta)\) | \(Z\) 軸 | 位相(角度)の操作。重ね合わせ状態にあるときの情報に直接働きかける。 |
この中で、本記事の主役である \(\text{R}_Z(\theta)\) ゲートは、その名のとおり \(Z\) 軸を中心に状態ベクトルを水平に回転させる役割を担います。
この回転は量子状態の位相情報を直接操作することに相当し、量子アルゴリズムの干渉制御において最も重要な役割を果たします。
1.1.3. \(R_Z\)ゲートのユニタリ行列と作用
本項で解説するユニタリ行列(数式)は、\(\text{R}_Z\) ゲートがなぜ位相操作を行うのかという物理的な根拠を示すために記述しています。
そのため、もし数式が難解だと感じても、Qiskitを使った量子プログラミングを進める上では、この行列を完全に理解する必要も覚える必要も一切ありません。
理解必須なのは、「1.1.3.2. Rzゲートの作用」だけですので、ご安心ください。
1.1.3.1. ユニタリ行列の定義(物理的な根拠)
\(\text{R}_Z(\theta)\) ゲートは、以下の \(2 \times 2\) 行列で定義されます。
\(U_{\text{Rz}}(\theta) = \begin{pmatrix} e^{-i\theta/2} & 0 \\ 0 & e^{i\theta/2} \end{pmatrix}\)
この行列を基底状態 \(|0\rangle\) や \(|1\rangle\) に作用させると、それぞれの状態に複素位相が乗じられます。
- \(U_{\text{Rz}}(\theta) |0\rangle = e^{-i\theta/2} |0\rangle\)
- \(U_{\text{Rz}}(\theta) |1\rangle = e^{i\theta/2} |1\rangle\)
\(|0\rangle\) と \(|1\rangle\) に付いた位相 \(e^{-i\theta/2}\) と \(e^{i\theta/2}\) の比率が、先述の相対的な位相のズレ \(\theta\) となることで、\(\text{R}_Z\) ゲートが位相操作を行うことが証明されます。
1.1.3.2. \(R_Z\)ゲートの作用(プログラミングに必須の知識)
\(\text{R}_Z\) ゲートの核心的な作用は、「重ね合わせ状態にある \(|1\rangle\) 側にだけ、相対的な位相のズレ \(\theta\) を導入する」ことです。
この「位相のズレ」が、次の項で解説する \(\text{H}\)-\(\text{R}_Z\)-\(\text{H}\) 回路における干渉、「強め合う(建設的干渉)」か、「打ち消し合う(破壊的干渉)」かのパターンを決定するトリガーとなります。
| 作用の結論 | 詳細な意味 |
|---|---|
| 振幅は不変 | 量子状態の確率(振幅の二乗)、測定結果の確率ともに変化しない。 |
| 位相のみ変化 | 量子状態の位相(角度)のみが変化する。 |
| 相対位相 | \(|0\rangle\) の状態と比較して、\(|1\rangle\) の状態に \(\theta\) 分のズレが生じる。 |
1.1.4. QiskitによるRzゲートの実行
Qiskitを使って\(\text{R}_Z\)ゲートを量子回路に組み込むコーディングは非常に簡単です。
以下の構文を使用します。
qc.rz(theta, qubit)| 要素 | 内容 |
|---|---|
qc | 初期化済の QuantumCircuit オブジェクト。 |
theta | \(\text{R}_Z\) ゲートに与える回転角度(ラジアン)。QiskitではNumPyの定数 \(\pi\) を使用するのが一般的です。 |
qubit | \(\text{R}_Z\) ゲートを適用する量子ビットのインデックス(整数)。 |
\(\text{R}_Z\) ゲートは単一量子ビットゲートであり、常に一つだけの量子ビットに作用します。
例えば、\(0\)番目の量子ビットに \(90^\circ\) の回転を適用する場合を考えてみましょう。
\(180^\circ\) が \(\pi\) ラジアンであるため、\(90^\circ\) は \(\pi/2\) ラジアンになります。
したがって、コードは以下のようになります。
from qiskit import QuantumCircuit
import numpy as np
qc = QuantumCircuit(1)
qc.rz(np.pi / 2, 0)1.2. \(R_Z\)が最も重要である理由
量子回転ゲートには \(\text{R}_X, \text{R}_Y, \text{R}_Z\) の3種類がありますが、量子アルゴリズムを理解し、構築する上で、\(\text{R}_Z\) ゲートは他の2つに比べて群を抜いて重要な役割を果たします。
このセクションでは、なぜ \(\text{R}_Z\) が最重要視されるのか、その理由を紐解きます。
1.2.1. 位相情報への直接アクセス
量子計算において最も強力な源泉は、量子状態の「位相(フェーズ)」に情報をエンコードし、それを利用する点にあります。
\(\text{R}_Z\) ゲートは、ブロッホ球の \(Z\)軸(極)を中心に状態を回転させるため、他のゲートのように状態ベクトル自体を大きく動かすことなく、重ね合わせ状態にある位相情報へ直接アクセスし、操作することができます。
位相操作が重要視される理由は次の2点に集約されます。
- 干渉の制御: 前セクションで確認した通り、\(\text{R}_Z\)は\(|0\rangle\)と\(|1\rangle\)の間に相対的な位相差 (\(\theta\)) を導入します。この位相差が、\(\text{H}\)ゲートと組み合わせた際に建設的干渉(確率を強める)と破壊的干渉(確率を打ち消す)を制御する唯一の手段となります。
- オラクル(Oracles)の構築:
量子アルゴリズムにおけるオラクルとは、古典的な関数 \(f(x)\) の計算ルールを量子回路で実装した「ブラックボックスの部品」です。- グローバー探索や位相推定のような強力なアルゴリズムでは、このオラクルによって、「答え」となる特定の状態にのみ、マイナス符号(\(\pi\)ラジアンの位相)を付与する操作(位相フリップ)が不可欠となります。
- \(\text{R}_Z\) ゲートは、この位相フリップ(\(\text{Z}\)ゲート \(=\) \(\text{R}_Z(\pi)\))を生成するための基本的な構成要素であり、これが\(\text{R}_Z\)が位相制御の核心である最大の理由です。
1.2.2. \(\text{R}_Z\) ゲートがあれば、他の単一量子ビット操作は合成可能
\(\text{R}_Z\) ゲートが\(\text{R}_X\)や\(\text{R}_Y\)に比べて優位とされる理由は他にもあります。
それは、\(\text{R}_Z\)と\(\text{H}\)(アダマール)ゲートがあれば、\(\text{R}_X\)や\(\text{R}_Y\)を含むあらゆる単一量子ビット操作を表現できるという点です。
これは量子回路設計において、\(\text{R}_Z\)を「主要な回転操作」として扱い、\(\text{R}_X\)や\(\text{R}_Y\)を「補助的な回転操作」として位置づけられることを意味します。
1.2.2.1. 軸変換の原理
ブロッホ球において、\(\text{H}\)ゲートの役割は軸を変換することです。
- \(\text{H}\)ゲートを適用すると、\(X\)軸は\(Z\)軸に、\(Z\)軸は\(X\)軸に交換されます。
この性質を利用すれば、\(\text{R}_X\)の操作(\(X\)軸周りの回転)は、以下の手順により\(\text{R}_Z\)を使って合成できます。
- \(\text{H}\)ゲートで軸を変換する (\(\text{X} \leftrightarrow \text{Z}\))。
- \(\text{R}_Z\)を適用し、位相操作を行う。
- 再び\(\text{H}\)ゲートで軸を元に戻す。
1.2.2.2. 軸変換による合成式
\(\text{R}_X(\theta) = \text{H} \cdot \text{R}_Z(\theta) \cdot \text{H}\)
\(\text{R}_Y(\theta) = \text{S}^{\dagger} \cdot \text{H} \cdot \text{R}_Z(\theta) \cdot \text{H} \cdot \text{S}\)
このように、\(\text{R}_Z\)と\(\text{H}\)(および\(\text{S}\)ゲートなどの\(\text{R}_Z\)派生ゲート)が組み合わさることで、全ての単一量子ビット回転操作が可能になります。
このため、\(\text{R}_Z\)は量子回路のミニマルな構成要素(ユニバーサルゲートセット)として非常に重要視されるのです。
第2章:\(\text{R}_Z\)ゲートによる干渉制御プログラミング
前章では、\(\text{R}_Z\)ゲートが位相(角度)をアナログに操作する、量子計算の核心的なゲートであることを確認しました。
しかし、\(\text{R}_Z\)ゲートを単独で適用しただけでは、測定結果の確率は変化しません。
その操作の効果を「観測可能」にするためには、\(\text{R}_Z\)ゲートによる位相のズレを振幅(確率)に変換する必要があります。
本章では、その変換を可能にする量子的な干渉の原理を解説するとともに、機能を実装することによって実践的に体験します。
Qiskitを使って実装する内容は、\(\text{H}\)-\(\text{R}_Z(\theta)\)-\(\text{H}\)という最も基本的な回路を構築し、\(\text{R}_Z\)ゲートの位相を制御します。
2.1. 干渉制御を実現する\(\text{H}\)-\(\text{R}_Z\)-\(\text{H}\)回路
2.1.1. 位相のズレを確率に変換する
\(\text{R}_Z\) ゲートが単独で適用された状態では、位相のズレは生じても、測定結果の確率は変化しないことを確認しました。なぜなら、位相はブロッホ球の表面で水平に回るだけで、北極と南極を結ぶ \(Z\) 軸上の投影(測定される確率)は変わらないからです。
位相の情報を確率として取り出すには、干渉の原理を利用する必要があります。
この干渉を実現するのが、\(\text{R}_Z\) ゲートを\(\text{H}\)(アダマール)ゲートで挟むという非常にシンプルな回路です。
\(\text{H} \to \text{R}_Z(\theta) \to \text{H}\)
2.1.1.1. 最初の\(\text{H}\)ゲート:重ね合わせの作成
まず、初期状態 \(|0\rangle\) に最初の\(\text{H}\)ゲートを適用することで、量子ビットは均一な重ね合わせ状態 \(|+\rangle = \displaystyle\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\) になります。
2.1.1.2. \(\text{R}_Z(\theta)\)ゲート:位相のズレの導入
ここで真打の登場、重ね合わせ状態に \(\text{R}_Z(\theta)\) ゲートを適用します。
これにより、\(|1\rangle\) 側にのみ \(\theta\) 分の位相のズレが導入されます。
これが干渉の「種」となります。
\(\text{R}_Z(\theta) |+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + e^{i\theta}|1\rangle)\)
2.1.1.3. 最後の\(\text{H}\)ゲート:位相の確率への変換
最後に、2回目の\(\text{H}\)ゲートを適用します。
この\(\text{H}\)ゲートは、位相のズレを振幅(確率)へと変換する役割を果たします。
干渉計算の結果、最終的な測定確率は \(\theta\) によって以下のように変化します。
以下は、繰り返し使用して覚えておきたい重要な数式です。
- 測定結果 \(|0\rangle\) となる確率 \(P(0)\): \(\cos^2(\theta/2)\)
- 測定結果 \(|1\rangle\) となる確率 \(P(1)\): \(\sin^2(\theta/2)\)
この回路は、入力された位相 \(\theta\) をコサイン二乗およびサイン二乗の関数として出力確率に変換する、「位相センサー」として機能します。
2.1.2. \(\text{H}\)-\(\text{R}_Z\)-\(\text{H}\)回路の実装(理論値\(\theta=0\))
位相制御の実験に入る前に、\(\text{H}\)-\(\text{R}_Z(\theta)\)-\(\text{H}\)回路において位相 \(\theta\) が \(0\) の場合の動作を確認します。
2.1.2.1. 理論値の予測 (\(\theta=0\))
前セクションの「2.1.1.3.」で示した確率の式に \(\theta=0\) を代入します。
- 測定結果 \(|0\rangle\) となる確率 \(\text{P}(0)\): \(\cos^2(0/2) = \cos^2(0) = 1^2 = 1.0\)
- 測定結果 \(|1\rangle\) となる確率 \(\text{P}(1)\): \(\sin^2(0/2) = \sin^2(0) = 0^2 = 0.0\)
理論上、\(\theta=0\)、つまり\(\text{R}_Z\)ゲートが何も操作しない場合、最終的に測定結果は必ず \(|0\rangle\) になる確率が 100% と予測されます。
\(\sin(0)\) と \(\cos(0)\) の違い
三角関数である \(\sin\)(サイン)と \(\cos\)(コサイン)は、直角三角形の比や、単位円上の座標として定義されます。
前提知識として、\(\sin(\theta)\) は \(Y\) 座標を意味し、\(\cos(\theta)\) は \(X\) 座標を意味することを覚えておきましょう。
- \(\sin(0)\) の値: 角度 \(\theta\) が \(0\) ラジアン(または \(0\) 度)のとき、\(\sin(\theta)\) の値は \(0\) です。
- \(\cos(0)\) の値: 一方、角度 \(\theta\) が \(0\) ラジアン(または \(0\) 度)のとき、\(\cos(\theta)\) の値は \(1\) です。
単位円(半径1の円)を使うことで直感的理解がしやすくなります。
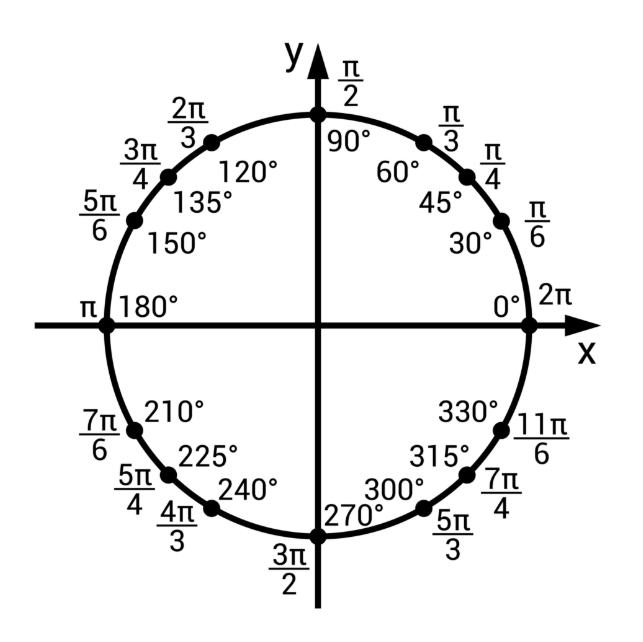
- 角度 \(0\) の位置は、円周上の最も右側(座標 \((1, 0)\))です。
- このとき、\(\cos(\theta)\) は \(X\) 座標を意味し、単位円は半径が 1 であるため \(X\) 座標は \(1\) です。
- \(\sin(\theta)\) は \(Y\) 座標を意味し、\(0\) です。
2.1.2.2. Qiskitによる回路の構築と実行
この理論値を検証するため、Qiskitを使って回路を構築します。
この段階で、実行環境(Sampler)と実行回数(shots)の設定が必要となります。
ここでは counts のみを取得するので、SamplerV2 ではなく Sampler (V1) を使用します。
import numpy as np
from qiskit import QuantumCircuit
from qiskit_aer.primitives import Sampler
# --- 1. 定数の設定 ---
THETA = 0.0 # 回転角度: 0ラジアン
SHOTS = 1024 # 実行回数
# --- 2. 回路の構築 (H-Rz(0)-H) ---
qc = QuantumCircuit(1, 1) # 1量子ビット, 1古典ビット
qc.h(0) # (1) 最初のHゲート: 重ね合わせを作成
qc.rz(THETA, 0) # (2) Rz(0): 位相操作 (操作なし)
qc.h(0) # (3) 最後のHゲート: 干渉による確率への変換
qc.measure(0, 0) # 量子ビット0を古典ビット0に測定
# --- 3. Samplerによる実行と結果の取得 ---
sampler = Sampler()
job = sampler.run(qc, shots=SHOTS)
result = job.result()
quasi_dist = result.quasi_dists[0]
# --- 4. 結果の表示と検証 ---
# QuasiDistributionをQiskit標準のcounts形式に変換
counts = {
format(k, 'b').zfill(qc.num_qubits): int(v * SHOTS)
for k, v in quasi_dist.items()
}
print(f"実行回数: {SHOTS}")
print(f"測定結果: {counts}")
# 期待される出力: {'0': 1024}
実行回数: 1024
測定結果: {'0': 1024}2.1.3. 破壊的干渉の実験(理論値\(\theta=\pi\))
次に、\(\text{R}_Z\) ゲートによる位相のズレが最大となる \(\theta = \pi\) ラジアンの場合を考えます。
この設定は、\(\text{R}_Z\) ゲートが\(\text{Z}\)ゲートと等価になり、位相フリップが発生する状態です。
【用語解説:位相フリップ(Phase Flip)】
位相フリップとは、量子状態の位相が \(180^\circ\) (\(\pi\)ラジアン) 回転することで、波の符号が反転する(プラス \(+\) がマイナス \(-\) になる)現象を意味します。
数学的には \(e^{i\pi} = -1\) であるため、位相が \(\pi\) ズレることは、その状態に \(-\) を掛けることと等価になります。
2.1.3.1. 理論値の予測 (\(\theta=\pi\))
前セクションの「2.1.1.3.」で示した確率の式に \(\theta=\pi\) を代入します。
- 測定結果 \(|0\rangle\) となる確率 \(\text{P}(0)\): \(\cos^2(\pi/2) = 0^2 = 0.0\)
- 測定結果 \(|1\rangle\) となる確率 \(\text{P}(1)\): \(\sin^2(\pi/2) = 1^2 = 1.0\)
この結果も、前述の「単位円」を使えば分かりやすいです。
\(\sin(\theta)\) は \(Y\) 座標を意味し、\(\cos(\theta)\) は \(X\) 座標を意味するんでしたよね。
今回の場合、\(\pi\) を数式に当てはめると、両者とも \(\pi/2\) ラジアンとなるため、\(90^\circ\) を見れば良いということになります。
理論上、\(\theta=\pi\) の場合は、最終的に測定結果は必ず \(|1\rangle\) になる確率が \(100\%\) と予測されます。
これは、最初の\(\text{H}\)ゲートで \(|0\rangle\) と \(|1\rangle\) の波が作られた後、\(\text{R}_Z(\pi)\)によって位相が完全に逆転(破壊)され、最後の\(\text{H}\)ゲートで \(|0\rangle\) へ戻る経路が打ち消されたことを意味します。
2.1.3.2. Qiskitによる回路の構築と実行
\(\theta = \pi\) の理論値を検証するため、前セクションの「2.1.2.2.」で作成したコードの定数 THETA のみを変更して実行します。
Python で \(\pi\) を使うには、NumPyというライブラリに用意されている定数を使用します。
作成したプログラムではNumPyは「np」という名前でインポートされているため、np.pi とコーディングすればOKです。
import numpy as np
from qiskit import QuantumCircuit
from qiskit_aer.primitives import Sampler
# --- 1. 定数の設定 ---
THETA = np.pi # 👈 回転角度: πラジアン に変更するだけです。
SHOTS = 1024 # 実行回数
# --- 以降のコードには変更ないため省略 ---
# 期待される出力: {'1': 1024} 実行回数: 1024
測定結果: {'1': 1024}2.1.4. 建設的干渉と破壊的干渉の分水嶺(理論値\(\theta=\pi/2\))
最後に、\(\theta=0\)(完全な建設的干渉)と \(\theta=\pi\)(完全な破壊的干渉)のちょうど中間地点にあたる、\(\theta = \pi/2\) (\(90^\circ\)) の場合を実験します。
この角度は、干渉効果が拮抗する分水嶺となります。
2.1.4.1. 理論値の予測 (\(\theta=\pi/2\))
前セクションの「2.1.1.3.」で示した確率の式に \(\theta=\pi/2\) を代入します。
ここでの計算には、\(\cos(\pi/4) = 1/\sqrt{2}\) という三角関数の性質を使います。
- 測定結果 \(|0\rangle\) となる確率 \(\text{P}(0)\): \(\cos^2(\pi/4) = (1/\sqrt{2})^2 = 0.5\)
- 測定結果 \(|1\rangle\) となる確率 \(\text{P}(1)\): \(\sin^2(\pi/4) = (1/\sqrt{2})^2 = 0.5\)
理論上、\(\theta=\pi/2\) の場合は、\(|0\rangle\) と \(|1\rangle\) が観測される確率はそれぞれ \(50\%\) となります。
これは、位相のズレが「戻る力(建設)」と「進む力(破壊)」のいずれにも偏らず、結果が完全にランダムになる状態です。
2.1.4.2. Qiskitによる回路の構築と実行
\(\theta = \pi/2\) の理論値を検証するため、前セクションの「2.1.2.2.」で作成したコードの定数 THETA のみを変更して実行します。
import numpy as np
from qiskit import QuantumCircuit
from qiskit_aer.primitives import Sampler
# --- 1. 定数の設定 ---
THETA = np.pi / 2 # 👈 回転角度: π/2ラジアン に変更するだけです。
SHOTS = 1024 # 実行回数
# --- 以降のコードには変更ないため省略 ---
# 期待される出力例: {'0': 512, '1': 512} 付近のランダムな値 実行回数: 1024
測定結果: {'1': 512, '0': 512}
# 何度か実行すると、以下ように若干の差異が出る場合があります
測定結果: {'1': 499, '0': 525}
測定結果: {'1': 515, '0': 509}第3章:まとめ — 位相制御が拓く世界
本記事では、「回転ゲート三部作」の第1部として、量子アルゴリズムにおける位相操作の要である \(\text{R}_Z(\theta)\) ゲートを解説しました。
\(\text{R}_Z\) ゲートが単にブロッホ球上で状態を回すだけでなく、\(\text{H}\) ゲートと組み合わせることで干渉を引き起こし、見えない「位相」の情報を見える「確率」へと変換できることを、理論とQiskitによる実験の両面から確認できたかと思います。
この「位相を操作して確率を制御する」という技術は、量子探索や量子化学計算など、あらゆる高度な量子アルゴリズムの基礎となるものです。
3.1. 今回の要点:\(\text{R}_Z\)ゲートと干渉
本記事の重要ポイントを整理します。
- \(\text{R}_Z\)は位相を操る: \(\text{R}_Z(\theta)\) ゲートは、量子状態の確率(振幅)を変えることなく、位相(角度)のみを精密に操作します。具体的には、\(|0\rangle\) に対して \(|1\rangle\) 側に \(\theta\) 分の相対位相を与えます。
- 干渉には「ハンバーガー」が必要: 位相の変化を測定可能な「確率の変化」として取り出すためには、\(\text{R}_Z\) ゲートを 2つの \(\text{H}\) ゲートで挟んだ \(\text{H}\)-\(\text{R}_Z\)-\(\text{H}\) 回路が必要です。
- 角度 \(\theta\) が結果を決める:
- \(\theta = 0\): 位相ズレなし。波が強め合い、初期状態 \(|0\rangle\) が再構成される(建設的干渉)。
- \(\theta = \pi\): 位相フリップ(符号反転)。波が打ち消し合い、\(|0\rangle\) が消失して \(|1\rangle\) になる(破壊的干渉)。
3.2. 次回予告:\(\text{R}_Y\)ゲートと状態準備
今回は位相(\(\text{Z}\)軸周り)の制御に集中しましたが、次回「第2部」では、ブロッホ球の経度方向、つまり\(\text{Y}\)軸周りの回転を制御する \(\text{R}_Y(\theta)\) ゲートを扱います。
\(\text{R}_Y\) ゲートは、ベクトルを動かさない \(\text{R}_Z\) とは異なり、初期状態 \(|0\rangle\) のベクトルをZ軸から大きく傾け、任意の確率振幅を持つ重ね合わせ状態を作り出す(状態準備)ために不可欠なゲートです。
次回は、\(\text{R}_Y\) ゲートを使って、量子ビットを自在に「傾ける」方法をマスターしましょう。



コメント