量子コンピューティングにおける最も基本的かつ重要な操作、量子回転ゲート。
この三部作の最終譚である本記事では、残された最後の回転軸、\(\text{R}_X\) ゲートを解説します。
第1部では\(\text{R}_Z\) ゲートによる「位相の制御」、第2部では\(\text{R}_Y\) ゲートによる「振幅の制御」をマスターしました。
\(\text{R}_X\) ゲートの役割は、\(\text{R}_Y\) ゲートがY軸周りの回転を担うように、X軸周りの回転を担うことです。
この$\text{R}_X$ ゲートを理解することで、これまで個別に見てきた\(\text{R}_Y\)、\(\text{R}_Z\) の各操作が、ブロッホ球上の任意の操作を可能にする「三次元の回転軸」として統合されることがわかります。
本記事を通して、\(\text{R}_X\) ゲートの操作方法、行列表現、そして他のゲートとの関係を習得し、単一量子ビットを意図通りに操作する技術を完全に掌握しましょう。
目次
第1章:\(\text{R}_X\) ゲートの操作と行列表現
1.1. \(\text{R}_X\) ゲートの役割と定義
\(\text{R}_X\) ゲートは、量子状態をX軸(ブロッホ球の赤道上)周りに回転させる単一量子ビットゲートです。
\($\text{R}_Y\) ゲートと同様に、\(\text{R}_X\) ゲートもまた、基底状態 \(|0\rangle\) と \(|1\rangle\) の振幅(測定確率)を変化させる上で不可欠な要素です。
しかし、両者の行列表現の違いからわかるように、\(\text{R}_X\) ゲートは\(\text{R}_Y\) ゲートとは異なり、操作の結果に虚数単位 \(i\) を伴い、同時に状態の位相にも影響を与えるという特徴を持ちます。
\(\text{R}_X(\theta) = \begin{pmatrix} \cos(\theta/2) & -i \sin(\theta/2) \\ -i \sin(\theta/2) & \cos(\theta/2) \end{pmatrix}\)
\(\text{R}_Y(\theta) = \begin{pmatrix} \cos(\theta/2) & -\sin(\theta/2) \\ \sin(\theta/2) & \cos(\theta/2) \end{pmatrix}\)
それぞれの行列表現を比較すると、以下のことが分かります。
- \(\text{R}_X(\theta)\): 虚数単位 \(i\) を含む。振幅と位相の両方に影響を与える。
- \(\text{R}_Y(\theta)\): 全要素が実数。主に振幅を制御する。
1.2. \(\text{R}_X\) ゲートの作用(基礎)
\(\text{R}_X\) ゲートの具体的な作用を理解するため、最も基本的な動作である、X軸周りの180度回転を見てみましょう。
初期状態 \(|0\rangle\) に \(\text{R}_X(\pi)\) ゲート(\(\pi\) ラジアン=180度)を適用すると、ブロッホ球上の状態は \(|0\rangle\)(Z軸の北極)から\(\text{X}\) 軸周りに回転し、最終的に \(|1\rangle\)(Z軸の南極)の状態に到達します。
この動作は、\(\text{R}_Y(\pi)\) ゲートが \(|0\rangle\) を \(|1\rangle\) に変換する振幅の制御として機能するのと非常に似ています。
しかし、\(\text{R}_X\) ゲートの操作は\(\text{R}_Y\) ゲートとは異なり、状態の位相(複素数の情報)に必ず影響を与えます。
- \(\text{R}_Y(\pi)\) の結果: \(|1\rangle\) (純粋な振幅の反転)
- \(\text{R}_X(\pi)\) の結果: \(-i|1\rangle\) (振幅の反転と位相の変化)
この操作によって生じる虚数単位 \(-i\) は、測定確率自体には影響しませんが、他のゲート(特に\(\text{R}_Z\))と組み合わせた際に重要な意味を持ちます。
1.3. \(\text{R}_X\) ゲートと\(\text{X}\) ゲートの関係
\(\text{R}_X\) ゲートは、与える角度 \(\theta\) の値によって様々な機能を発揮しますが、その最も重要な応用例は、特定の角度でパウリ \(\text{X}\) ゲート(量子NOTゲート)の機能を含む点です。
- 要点: \(\text{R}_X\) ゲートに \(\theta = \pi\)(180度)の回転角を与えると、\(\text{X}\) ゲートとグローバル位相を除いて等価になります。
- \(\text{X} \approx \text{R}_X(\pi)\)
- 役割: \(\text{X}\) ゲートが固定された\(180^\circ\)の反転操作であるのに対し、\(\text{R}_X\) ゲートは\(\text{X}\) 軸周りの任意の角度の回転を可能にする、汎用的なツールです。
1.4. \(\text{R}_X\) と \(\text{X}\)、\(\text{H}\) ゲートの使い分け
実用的な量子プログラミングにおいて、\(\text{R}_X\)、\(\text{X}\)、そして\(\text{H}\) ゲートはどのように使い分けられるのでしょうか?
この使い分けの基準は、主に「操作の柔軟性」と「必要な角度」などによって決まります。
- \(\text{X}\) ゲートを使うケース(シンプルな反転)
- 確定的なビット反転(NOT操作)が必要な場合は、回路の意図が明確で可読性が高いため、\(\text{R}_X(\pi)\) ではなく\(\text{X}\) ゲートを使います。
- \(\text{H}\) ゲートを使うケース(固定の重ね合わせ)
- \(50%\)ずつの均等な重ね合わせ状態を作る場合は、最もシンプルで効率的な\(\text{H}\) ゲートを使います。
- \(\text{R}_X\) でなければならないケース(任意の重ね合わせ)
- \(\text{R}_X\) ゲートが不可欠となるのは、任意の測定確率を持つ重ね合わせ状態(例:\(\text{P}(1)=75\%\))を作りたい場合です。
- \(\text{H}\) ゲートや\(\text{X}\) ゲートでは不可能な、\(\text{X}\) 軸周りの任意の角度の回転を可能にします。
第2章:【実装の核心】測定前・後の状態と二重回路の必要性
2.1. 二重回路の物理的必然性
第1章で、\(\text{R}_X\) ゲートの持つ位相(虚数成分)という量子計算の複雑な側面を学びました。
この「目に見えない情報」を正確に検証するには、従来のプログラミングとは異なる、特殊な検証方法が必要です。
このセクションでは、その特殊な方法、すなわち「二重回路の原則」を確立するために不可欠な、物理的な根拠と、その帰結として求められるプログラミング上の必須の検証視点を明確にします。
2.1.1. 量子状態の収縮と情報損失(二重回路の物理的根拠)
\(\text{R}_X\) ゲートの実装に進む前に、量子プログラミングにおける最も重要な物理的な制約を明確に理解する必要があります。
量子力学には、測定を行うとその瞬間に量子ビットの重ね合わせ状態が壊れ、観測された状態に確定する(収縮する)という、根本的な制約があります。
この原理が、プログラミングにおいて以下の2つの不可逆的な情報損失を引き起こします。
- 状態の破壊: 一度測定を実行すると、その量子ビットは二度と重ね合わせ状態に戻りません。
- 位相の消失: \(\text{R}_X\) ゲートが生成する位相(虚数成分)という量子情報が、測定によって完全に失われます。
したがって、私たちはこの情報損失を避けるために、測定前の状態(位相を含む)を確認するプログラムと、測定後の確率を確認するプログラムを物理的な必然性から分けて作る必要があるのです。
この原則は、\(\text{R}_X\) に限らず、\(\text{H}\) ゲートや \(\text{CX}\) ゲートなどすべての量子操作に共通する、普遍的な前提知識です。
前回記事の \(\text{R}_Y\) を含む、これまでのゲートはシンプルなケースであったため、複雑な位相の問題を回避し、敢えて原則を明文化していませんでした。
しかし、\(\text{R}_X\) ゲートは虚数成分(位相)を生成するため、測定では見えない情報が問題として浮き彫りになります。
2.1.2. 検証に必要な2つの視点と回路の使い分け
量子回路の検証では、物理的な制約により、測定前の状態と測定後の確率という2つの視点から、異なる情報を得る必要があります。
それを実現するため、Qiskitのシミュレーターと回路(QuantumCircuit オブジェクト)を意図的に使い分けます。
この使い分けが、次の項で実装する二重回路の原則の具体的な実装方法となります。
2.1.2.1. 測定前の視点:状態ベクトルによる検証 (プログラム1の設計)
\(\text{R}_X\) ゲートがベクトルをどこに回転させ、どのような位相を生成したかという、ゲートの数学的な定義に基づいた完全な操作を検証する視点です。
| 項目 | 詳細 | プログラミング上の対応 |
|---|---|---|
| 回路の目的 | 測定による収縮を避ける | 測定コマンド (.measure()) を含まない |
| 確認できる情報 | 状態ベクトル (位置と位相) | ブロッホ球による視覚化 |
| シミュレーター | statevector_simulator | 理想的な重ね合わせの状態を計算 |
2.1.2.2. 測定後の視点:ヒストグラムによる検証 (プログラム2の設計)
その状態を測定した場合に観測される確率が、設計通り(例:\(\text{Y}\) 軸上の状態であれば \(50\% / 50\%\))になっているかを検証する視点です。
| 項目 | 詳細 | プログラミング上の対応 |
|---|---|---|
| 回路の目的 | 確率的な収束をシミュレートする | 測定コマンド (.measure()) を含める |
| 確認できる情報 | \(|0\rangle\) と \(|1\rangle\) の(観測確率) | ヒストグラムによる視覚化 |
| シミュレーター | qasm_simulator | 多数回の試行(ショット)による統計的な確率を計算 |
2.2. 測定前の回路構築とブロッホ球の描画(プログラム1)
ここでは、二重回路の原則に基づき、まず測定による収縮を起こさせない回路を構築します。
このプログラムの目的は、\(\text{R}_X(\pi/2)\) ゲートが\(\text{Z}\) 軸上の初期状態を\(\text{Y}\) 軸上に正しく回転させたか、つまり位相情報も含めた完全な操作が行われたかを検証することです。
2.2.1. ライブラリのインポート
まずは、量子回路の構築と実行、そしてブロッホ球の描画に必要なライブラリをインポートします。
from qiskit import QuantumCircuit
from qiskit_aer import Aer
from qiskit.visualization import plot_bloch_multivector
import numpy as np
import matplotlib.pyplot as plt2.2.2. 測定を含まない回路の構築
「状態の収縮を防ぐ」という目的のため、測定コマンドを含まない回路オブジェクト qc_state を構築します。
初期状態 \(|0\rangle\) に \(\theta = \pi/2\)(\(90^\circ\))の回転角を持つ\(\text{R}_X\) ゲートを量子ビット0に適用します。
# 1. 測定コマンドを含まない回路 (状態ベクトル確認用)
qc_state = QuantumCircuit(1)
# R_X(pi/2)を適用 (X軸周りに90度回転)
# 初期状態|0>が、Y軸上の状態に移動することを確認します。
qc_state.rx(np.pi/2, 0)
# 完成した回路図の確認 (視覚的にゲートの適用を確認)
qc_state.draw('mpl')
plt.show() # 回路図を画面に表示する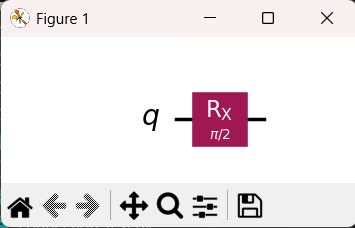
回路図の画像が表示されます。
測定(measure)処理を行っていないため、メーターアイコンが描画されていないことが分かります。
2.2.3. 状態ベクトルの取得と分析
構築した測定を含まない回路 qc_state を実行し、状態ベクトルを取得します。
前回記事では、Statevector(qc) を使っていましたが、今回は Aer.get_backend() 形式を採用します。
後のヒストグラム検証(プログラム2)で異なるシミュレーター(バックエンド)を使用する必要があるため、Aer.get_backend()を使用することで構造的な一貫性を保つことができます。
2.2.3.1. シミュレーターの実行コード
Aer.get_backend() の引数として、理想的な重ね合わせの状態を計算するシミュレーター (statevector_simulator) を指定します。
# 2. statevector_simulator で実行
simulator_state = Aer.get_backend('statevector_simulator')
job_state = simulator_state.run(qc_state, shots=1)
statevector = job_state.result().get_statevector()
# 結果の確認 (状態ベクトルの出力)
print(np.asarray(statevector).round(5))[0.70711+0.j 0. -0.70711j]2.2.3.2. 実行結果(状態ベクトル)の物理的意味
ここでは、前項で得られた実行結果の状態ベクトルが、\(\text{R}_X(\pi/2)\) ゲートによってどのように変換されたかを解釈します。
\(\text{R}_X(\theta)\) ゲートが初期状態 \(|0\rangle\) に作用したとき、結果を最も簡単に解釈する方法は、量子ビットの順序(\(|0\rangle, |1\rangle\))を意識し、虚数 $i$ が付いている場所と符号を確認することです。
- 最初の数値 (0.70711+0.j): \(|0\rangle\)の項
- 虚数部が \(0.j\) (数学でいう \(0 \times j\)) なので、実数のみと判断できる
- 二番目の数値 (-0.70711j): \(|1\rangle\)の項
- \(j\) が存在し、\(\text{X}\) 軸周りの回転を意味する
\(j\) の項の符号がマイナスなので、\(\text{Y}\) 軸の負の位置に回転した。
※ rxの引数には正の数 (\(np.pi/2\)) を渡しているため、正の方向に向かって回転したが、着地点が負の位置だったということになります。
| ゲート | \(|0\rangle\) の係数 | \(|1\rangle\) の係数 | 回転平面 |
|---|---|---|---|
| R\(_X\) | 実数のみ | 虚数 | \(\text{Y}-\text{Z}\) 平面内を移動 |
| R\(_Y\) | 実数のみ | 実数のみ | \(\text{X}-\text{Z}\) 平面内を移動 |
| R\(_Z\) | 虚数 | 実数のみ | \(\text{X}-\text{Y}\) 平面内を移動 |
各ゲートの係数につく符号の役割は以下の通りです。
- R\(_X\), R\(_Y\): 係数の符号(または虚数 \(j\) の符号)は、状態が回転平面内の正負どちらの位置に着地したかを決定します。
※ 回転する方向は、ゲートに渡す「引数(角度)」の符号で決まります。 - R\(_Z\) ゲート: R\(_Z\) の符号は、量子状態の物理的な変化を示す「相対位相」、または観測に影響しない「グローバル位相」のいずれかとして現れます。
2.2.4. ブロッホ球の描画による視覚化
状態ベクトル \(|\psi\rangle\) がブロッホ球上のどの位置にいるのかを視覚的に確認することは、状態の物理的な意味を直感的に理解する上で最も有効です。
ここでは、前の項で取得した状態ベクトル statevector を使って、ブロッホ球を描画します。
2.2.4.1. 描画のコード
Qiskitの plot_bloch_multivector 関数を使用することで、取得した状態ベクトルをブロッホ球上にマッピングできます。
# ブロッホ球の描画
plot_bloch_multivector(statevector)
plt.show()2.2.4.2. 実行結果と解釈
描画されたブロッホ球を見ると、状態ベクトルはX軸を中心に正の方向に回転し、Y軸の負の位置に移動したことが確認できます。
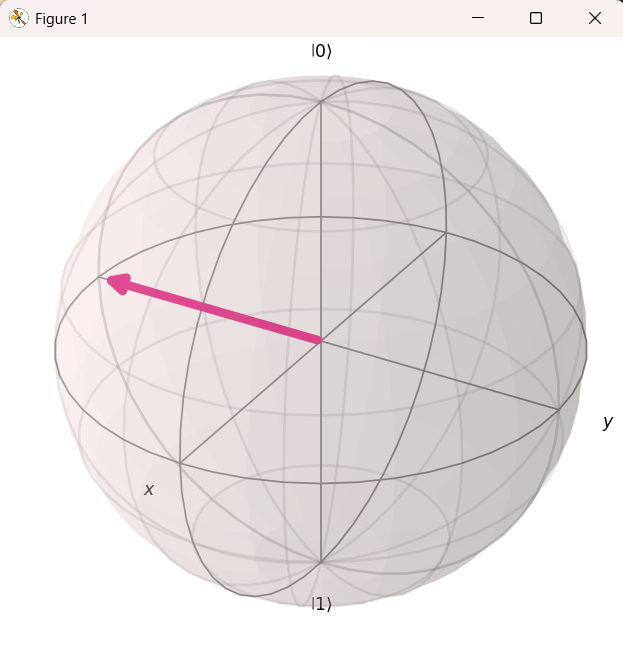
- 位置: \(\text{Y}\) 軸の負の極(\(|+Y\rangle\) 状態)
- 裏付け: これは、項2.2.3.2. での解析と完全に一致します。
2.3. 測定後の回路構築とヒストグラムの描画(プログラム2)
ここでは、二重回路の原則に基づき、\(\text{R}_X\) ゲートが生成した状態を実際に測定した後の確率を検証します。
このプログラムの目的は、理論的な測定確率(\(|0\rangle\) と \(|1\rangle\) が \(50\%\) ずつ)が、多数回の試行によって統計的に証明されることを示すことです。
2.3.1. 測定コマンドを含む回路の構築と実行
ここでは、「測定後の視点」を得るため、測定コマンド(.measure())と古典レジスタを追加した新しい回路オブジェクトを構築します。
from qiskit import QuantumCircuit
from qiskit_aer import Aer
from qiskit.visualization import plot_histogram
import numpy as np
import matplotlib.pyplot as plt
# 2. 測定コマンドを含む回路 (ヒストグラム確認用)
qc = QuantumCircuit(1, 1) # 量子ビット1、古典ビット1
# R_X(pi/2)を適用 (X軸周りに90度回転)
qc.rx(np.pi/2, 0)
# 測定コマンドを追加: 量子ビット0の結果を古典ビット0に格納
qc.measure(0, 0)
# 完成した回路図の確認
qc.draw('mpl')
plt.show() # 回路図を画面に表示する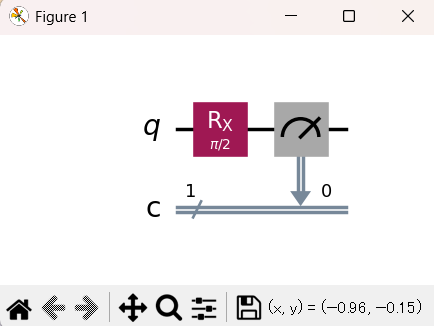
回路図の画像が表示されます 。
測定処理が追加されたため、2.2.2.では存在しなかったメーターアイコンが描画され、量子ビットが古典レジスタに接続されていることが確認できます。
2.3.2. 確率シミュレータの実行とヒストグラム描画
ここでは、前項で構築した測定コマンドを含む回路を使用し、多数回(shots=1024)の試行による統計的な確率を計算する qasm_simulator で実行します。
この結果をヒストグラムで視覚化することで、\(\text{R}_X(\pi/2)\) ゲートが設計通り \(50\% / 50\%\) の重ね合わせ状態を生成したことを証明します。
2.3.1 で作成したコードの下に続けて、以下のコードを追加してください。
# 3. qasm_simulator で実行
simulator = Aer.get_backend('qasm_simulator')
# shots=1024 (試行回数) を指定して実行
job = simulator.run(qc, shots=1024)
counts = job.result().get_counts(qc)
# 結果の確認 (測定回数の出力)
print(counts)
# 4. ヒストグラムの描画
plot_histogram(counts)
plt.show(){'1': 510, '0': 514}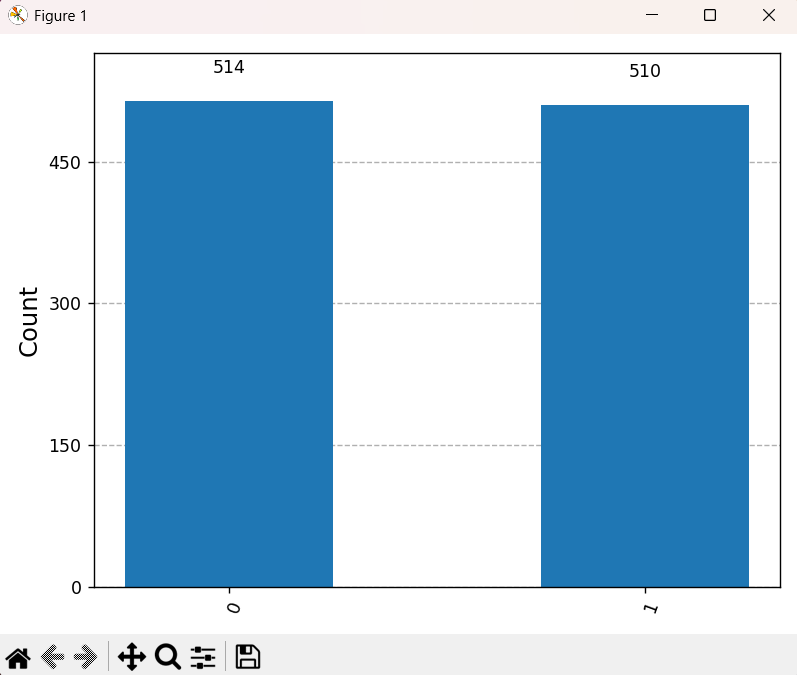
測定結果のコンソール出力、およびヒストグラムは、結果 '0' と '1' がほぼ半々の確率で得られることを示しています。
これにより、\(\text{R}_X\) が均等な重ね合わせ状態を作り出したことが確認できます。
まとめ
回転ゲート三部作の第1部で \(\text{R}_Z\) ゲートによる位相の制御を、第2部で \(\text{R}_Y\) ゲートによる振幅の制御を学び、本記事では \(\text{R}_X\) ゲートによるX軸周りの回転を学習しました。
\(\text{R}_X\), \(\text{R}_Y\), \(\text{R}_Z\) のこれら三つの回転ゲートは、ブロッホ球上の三次元空間における座標軸に完全に対応しています 。
今回記事の主役であった \(\text{R}_X\) ゲートは、\(\text{R}_Y\) ゲートとは異なり、操作の結果に虚数単位 \(i\)$ を伴います。
この虚数成分は、測定(ヒストグラム)からは直接観測できない位相(Phase)という情報を量子状態に与えます。
- 測定前の意味: \(\text{R}_X(\pi/2)\) で生成した状態 \(\frac{1}{\sqrt{2}}|0\rangle – \frac{i}{\sqrt{2}}|1\rangle\) は、ブロッホ球上の \(\text{Y}\) 軸の負の極に位置しますが、この虚数 \(i\) の符号(または有無)が、他のゲートと組み合わせた際に重要な干渉効果を生み出す鍵となります。
- 二重回路の意義: 第2章で実践した二重回路の原則は、この「目に見えない位相」をブロッホ球(測定前)で確認し、その結果がヒストグラム(測定後)の確率に結びついていることを示すために、物理的な必然性から必要不可欠でした。
次の目標: これまで個別に学んだ \(\text{R}_X\), \(\text{R}_Y\), \(\text{R}_Z\) の三つの回転ゲートは、量子ゲートにおける回転操作の全てを集約した、\(\mathbf{U}3\) ゲートへと統合されます。
次の記事では、この\(\mathbf{U}3(\theta, \phi, \lambda)\) ゲートをテーマとし、三つの独立したパラメータがブロッホ球上の任意の点を制御するプログラムを作成します。



コメント