「三角形の内角の和は180度である」。
私たちはこうした幾何学のルールを、当たり前の事実として受け入れています。
しかし、こういった「当たり前」に感じる事実にも、数学では証明が必要です。
そして、その証明の土台となる出発点は、たった10個のシンプルな前提に過ぎません。
本記事では、2000年以上前にユークリッドによって体系化された幾何学の原点に立ち返ります。
すべての数学的真実を論理的に積み上げていく、その最初のレンガとなる「公理(Axiom)」と「公準(Postulate)」について解説します。
誰の目にも明らかなこととは言え、なぜ証明もなしに正しいと決められたのか。
そして、その中の一つの前提(公準5)を疑うことで、現代科学を支える非ユークリッド幾何学という全く新しい世界が生まれた経緯を、基礎から見ていきましょう。
本記事で挙げている公理と公準は、私たちが中学・高校で学ぶ「ユークリッド幾何学」という体系を成立させるための土台です。
これらのルールは、非ユークリッド幾何学など、異なる前提を持つ数学体系には適用されません。
共通概念としての「公理」(5つ)
以下にリストアップする5つの公理は、幾何学に限らず、数学全般で通用すると考えられた基本的な性質です。
- 同じものに等しいものは、互いに等しい。
- \(A = C\) かつ \(B = C\) ならば \(A = B\) である。
- 等しいものに等しいものを加えても、和は等しい。
- \(A = B\) ならば \(A + C = B + C\) である。
- 等しいものから等しいものを引いても、差は等しい。
- \(A = B\) ならば \(A – C = B – C\) である。
- 互いに重なり合うものは、互いに等しい。
- 図形や線分を重ねて一致させることができれば、それらは等しい。
- 全体は部分より大きい。
- \(A\) が \(B\) の一部であれば、\(A\) は \(B\) より大きい。
幾何学固有の「公準」(5つ)
以下にリストアップする5つの公準は、図形や空間に関する基本的な前提です。
- 任意の点から任意の点へ直線を引くことができる。
- 有限の直線を制限なくまっすぐに延長することができる。
- 任意の中心と任意の半径をもって円を描くことができる。
- 全ての直角は互いに等しい。
- 直線と、その直線上にない一点が与えられたとき、その点を通って元の直線と平行な直線はただ一つ存在する。
平行と垂直の不思議
公準5の「直線と、その直線上にない一点が与えられたとき、その点を通って元の直線と平行な直線はただ一つ存在する。」に注目してください。
これが公準ならば、以下の性質も公準なのではないか、と思いませんか?
「直線と、その直線上にない一点が与えられたとき、その点を通って元の直線と垂直な直線はただ一つ存在する。」
はい、ユークリッド幾何学の体系においては、上記は正しいです。
ただし、この性質は、公準(証明なしの前提)として採用されているわけではありません。
上記の性質が公準ではない理由は、次の通りです。
ユークリッドの『原論』では、垂直線の存在と一意性(唯一であること)は、公理や公準から論理的に証明できる「定理」であると考えられています。
公準として採用されたのは、ユークリッドが他の単純な公理や公準だけでは証明が困難だと考えた事項でした(特に公準5の平行線の公準)。
では、垂直線の存在が一意であると証明できる根拠は何でしょうか。
垂直線の一意性(唯一であること)は、主に公準4(全ての直角は互いに等しい)や三角形の合同条件など、他の公理・公準を用いて証明されます。
証明の概要は以下の通りです。
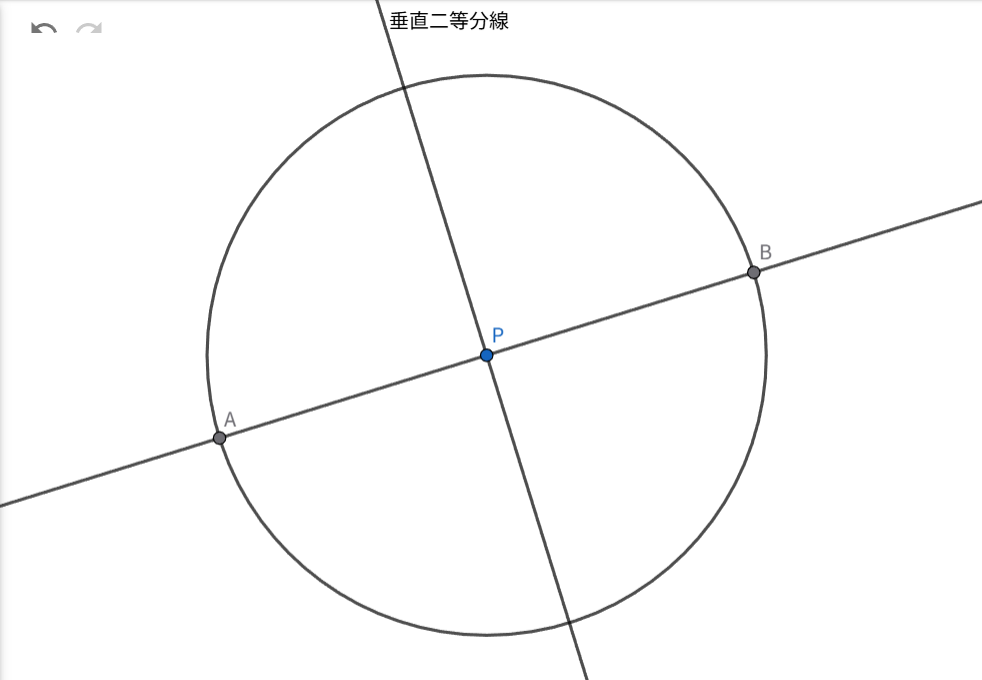
- 与えられた直線 \(L\) と点 \(P\) があります。
- 点 \(P\) を中心とする円を描き、直線 \(L\) と交わる2点 \(A\) と \(B\) を定めます(公準3、公準1)。
- 線分 \(AB\) の垂直二等分線を作図します。
- この垂直二等分線は直線 \(L\) と垂直になり、点 \(P\) を通ります。
- もし、点 \(P\) を通る垂直線が2本あったと仮定すると、直角が2つ存在する三角形ができてしまい、「三角形の内角の和は180度である」という定理(これも公理から証明される)に矛盾します。
したがって、「その点を通って元の直線と垂直な直線はただ一つ存在する」という事実は、公理・公準から導かれる定理であり、証明が必要な事柄なのです。
公理に限りなく近しいもう一つの定理
前述の垂直線の一意の性質の他にも、限りなく公理に近しい定理があります。
それは、「辺角辺(SAS)の合同条件」です。
※「SAS」とは、Side、Andle、Sideの頭文字をとった略称で、三角形の合同条件の一つを簡潔に表現するために国際的に使われている表記です。
- 2つの三角形において、2組の辺とその間の角がそれぞれ等しいならば、その2つの三角形は合同である。
これは、2つの三角形を重ね合わせる(公理4:互いに重なり合うものは等しい)ことで証明できます。
まとめ
本記事を通じて、幾何学のすべての知識が、たった10個の公理と公準というシンプルな前提から積み上げられていることを学びました。
- 公理・公準:証明を必要としない、論理体系の究極の出発点です。
- 定理:公理から論理的に証明された、新しい真実です(例:垂直線の一意性)。
この構造を理解することは、数学の面白さの原点です。
なぜなら、一見「当たり前」に見える事柄でも、その背後には論理的な証明の連鎖が隠されているからです。
特に、「平行線の公準」というたった一つの前提を疑うことで、時空のゆがみを扱う非ユークリッド幾何学が生まれ、物理学の様相を一変させました。
公理という土台が固まった今、次の段階は、この土台を使って新しい知識にアクセスすることです。
次回以降の記事では、公理や公準、あるいは既に証明された定理を基に、論理的に証明される「定理」を1つずつ紐解いていきたいと思います。



コメント