微分をゼロ以前のマイナス（前提）から徹底的に学ぶ

微分を理解するために必要は知識は何かと問えば、究極には四則演算まで遡ることになるでしょう。
本記事で扱う前提知識として、どこまで遡るか迷いましたが、「関数」からスタートしたいと思います。

関数とは、$y = f(x)$ です。

この数式は、「$x$ の値が 1 つに定まれば、 $y$ の値が決まる」という意味を持ち、「$y$ は $x$ の関数である」と表現します。

1 1. なぜ関数 $y = f(x)$ が微分の基礎となるのか
- 1.1 1.1. 変数間の関係を定義する
- 1.2 1.2. 微分の目的はその「変化」の分析
2 2. 変化を捉えるための第一歩：平均変化率
3 3. 瞬間の変化率へ：極限の考え方
4 4. 微分の定義式（導関数）の確立
- 4.1 4.1. 瞬間の変化率を表す数式
- 4.2 4.2. 導関数と記号
5 5. 定義式から導関数を導く：実践計算
6 6. 導関数を求めるための公式
7 7. 微分がプログラミングで役立つ3つの具体例
8 🔚 まとめ

1. なぜ関数 $y = f(x)$ が微分の基礎となるのか

微分とは「瞬間の変化率」を求める計算であるため、その対象となる「変化するもの」を明確にする必要があります。

それが関数 $y = f(x)$ です。
一見すると一次関数に見えますが、厳密には違います。

$y = f(x)$ は、関数の「型」であり、その内容が何であるかは定義で決定されます。
具体的には、$f(x) = x^2$ とすると、x の値を二乗する関数に変身するイメージです。

$y = f(x)$ 👈 関数の型

$f(x) = x^2$ 👈 関数の内容を定義している

$x = 3 \text{の場合}$ 👈 変数 $x$ に実際の値を代入している

$y = 3^2 = 9$ 👈 定義と実際の値をもって計算している

$\text{したがって} y = 9$

1.1. 変数間の関係を定義する

冒頭に述べた通り、関数 $y = f(x)$ は、「変数 $x$ の値が決まると、それに対応する変数 $y$ の値がただ一つ決まる」という関係を表します。

$x$（独立変数）: 原因や入力、操作する量
- 例：時間、商品の価格、学習の回数
$y$（従属変数）: 結果や出力、変化を観測する量
- 例：距離、売上、AIの誤差
$f$（関数）: $x$ を $y$ に変換するルールや計算式
- 例：$f(x) = x^2$ や $f(x) = \sin(x)$

1.2. 微分の目的はその「変化」の分析

微分（$\displaystyle\frac{dy}{dx}$）が求めるのは、「$x$がほんの少し変化したとき、$y$がどれだけ変化するか」という瞬間の変化の割合です。

この $x$ と $y$ の間の関係（$f(x)$）が明確でなければ、何を基準に、何の変化率を計算しているのかが分からなくなってしまいます。

2. 変化を捉えるための第一歩：平均変化率

微分が求める「瞬間の変化率」を理解する前に、よりシンプルで基本的な「平均の変化率」を理解することが不可欠です。

平均変化率とは、ある区間全体で見て、どれだけの割合で出力（$y$）が変化したかを示すものです。グラフ上では、関数の2点を結んだ直線の傾きに相当します。

2.1. 変化の量を記号で表す

まず、入力 $x$ と出力 $y$ の「変化の量」を定義します。
数学では、変化の量を表すためにギリシャ文字の$\Delta$（デルタ）を使います。

入力 $x$ の変化量: $\Delta x$ (デルタエックス)
出力 $y$ の変化量: $\Delta y$ (デルタワイ)

関数 $y = f(x)$ において、入力が $x_1$ から $x_2$ に変化したとき、変化量 $\Delta x$ と $\Delta y$ は次のように定義されます。

$\Delta x = x_2 – x_1$

$\Delta y = f(x_2) – f(x_1)$

2.2. 平均変化率の計算と直線の傾き

平均変化率は、「$x$ の変化量に対して、$y$ がどれだけ変化したか」の比率（割合）として定義されます。直線の傾きの計算とまったく同じですね。

$\text{平均変化率} = \displaystyle\frac{\text{y の変化量}}{\text{x の変化量}} = \displaystyle\frac{\Delta y}{\Delta x}$

これを関数 $f(x)$ を用いて表現すると、以下のようになります。

$\text{平均変化率} = \displaystyle\frac{f(x_2) – f(x_1)}{x_2 – x_1}$

この値は、グラフ上において、点 $(x_1, f(x_1))$ と点 $(x_2, f(x_2))$ の 2 点を結ぶ線分（割線）の傾きを表します。

2.3. 具体例：$f(x) = x^2$ の平均変化率

ここで、関数を $f(x) = x^2$ と定義し、具体的な平均変化率を計算してみましょう。

例：$x$ の値が 1 から 3 へ変化したときの平均変化率を求める

$x_1 = 1 \text{ 👉 } f(x_1) = 1^2 = 1$
$x_2 = 3 \text{ 👉 } f(x_2) = 3^2 = 9$

計算：$\Delta x$、$\Delta y$、平均変化率を求める

$\Delta x = x_2 – x_1 = 3 – 1 = 2$
$\Delta y = f(x_2) – f(x_1) = 9 – 1 = 8$
$\text{平均変化率} = \displaystyle\frac{\Delta y}{\Delta x} = \displaystyle\frac{8}{2} = 4$

結論

$x$ が 1 から 3 に変わる間、この関数の平均的な傾きは 4 であることが分かります。

2.4. 傾きをグラフで確認する

関数の定義は $f(x) = x^2$、$x$ の値が 1 から 3 へ変化したときの平均変化率を、今度はグラフで視覚的に確認してみましょう。

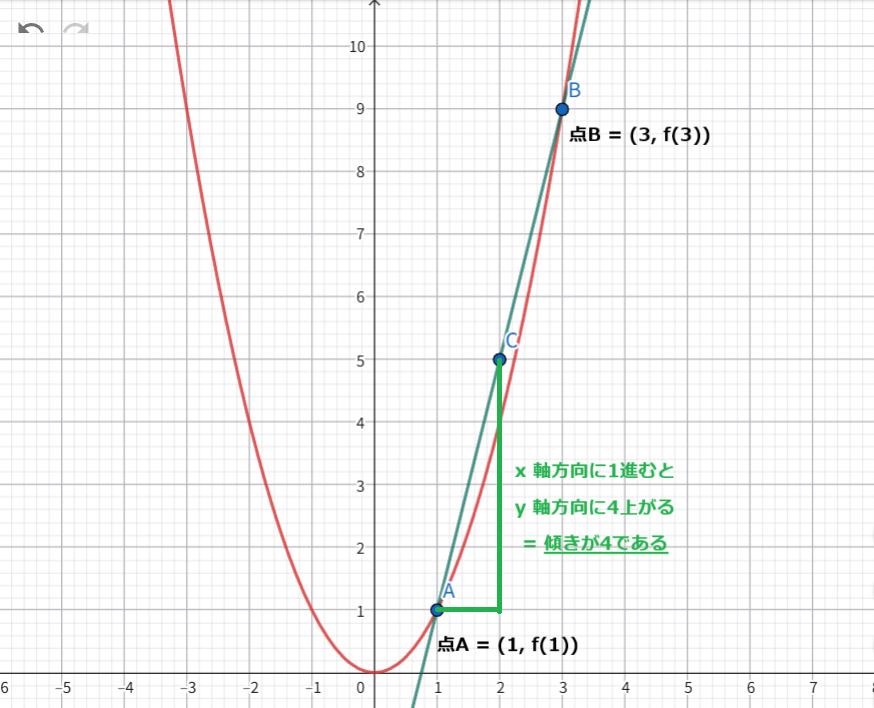
このように、平均変化率は計算によって、あるいはグラフ上で確認することができます。

3. 瞬間の変化率へ：極限の考え方

前章までで、ある区間 [$x_1$ から $x_2$] における関数の平均的な傾きを計算する平均変化率を学びました。
ここで、$\mathbf{\Delta x}$ は、$x$ の「変化量（区間の幅）」を表す記号です。

しかし、瞬間の変化率へ進むためには、この変化量 $\mathbf{\Delta x}$ を限りなくゼロに近づける操作が必要になります。

3.1. 「瞬間」の変化率計算が困難な理由

「瞬間」の変化率とは、$\Delta x$（$x$ の変化量）がゼロのときの変化率を意味します。
では、平均変化率の式に $\Delta x = 0$ をそのまま代入してみましょう。

すると、次のようになり、計算が破綻してしまいます。

$\text{平均変化率} = \frac{\Delta y}{\Delta x}$

$ = \frac{f(x + \Delta x) – f(x)}{\Delta x}$

$ \rightarrow \frac{f(x) – f(x)}{0} = \frac{0}{0}$

数学において、分母が $0$ になる計算（＝ゼロ除算）は禁じ手です。
この問題を回避し、瞬間を数学的に扱うために必要なのが、極限（Limit）という操作です。

3.2. 瞬間の変化を実現する「極限」の導入

極限 $\lim$ （リミット）とは、「限りなく近づける」という数学的に厳密な操作を意味します。
「$\Delta x$ がちょうど $0$ のとき」ではなく、「$\Delta x$ が限りなく $0$ に近づくとき、平均変化率はどのような値に収束するのか」を知ることができます。

また、極限の導入によって、分母が $0$ になる問題を回避し、非線形な関数の瞬間の傾きを計算可能になります。

この瞬間の変化率の関係を、極限記号 $\mathbf{\lim}$ を用いた定義式で表すと、以下のようになります。

$\text{瞬間の変化率} = \displaystyle\lim_{\Delta x \to 0} \displaystyle\frac{\Delta y}{\Delta x}$

3.3. 接線の傾きとして変化率を捉える

グラフ上では、極限操作 $\Delta x \to 0$ は次のような意味を持ちます。

平均変化率（割線）: はじめ、2つの点 A と B を結ぶ割線（平均の傾き）を考えます。
極限操作: 点B を、点A に向かって限りなく近づけていきます。言い換えれば、変化量 $\Delta x$ をどんどん小さくします。
瞬間の変化率（接線）: 点B が点A と一致する寸前、割線は点A で関数に接する一本の直線（接線）になります。

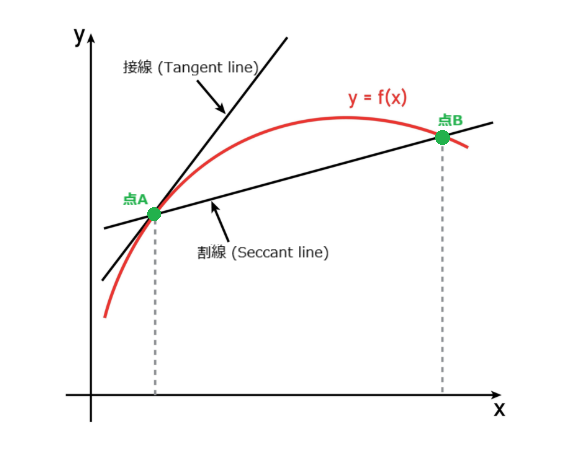
この接線の傾きが、まさしく点A における関数の「瞬間の変化率」であり、すなわち微分によって求められる値（極限値）となります。

4. 微分の定義式（導関数）の確立

関数の概念からスタートし、平均変化率（割線の傾き）、そして極限（瞬間への操作）を学んだことで、ついに微分を定義する厳密な数式を確立できます。

4.1. 瞬間の変化率を表す数式

微分の定義式は、以下の2つの要素を組み合わせたものです。

平均変化率: $\displaystyle \frac{f(x + \Delta x) – f(x)}{\Delta x}$
極限操作: $\lim_{\Delta x \to 0}$

この極限操作を平均変化率に適用することで、ある一点 $x$ における、瞬間の変化率を示す新しい関数が生まれます。

この瞬間の変化率を表す新しい関数が微分の定義式であり、導関数（どうかんすう）と呼ばれます。

$\text{導関数（微分の定義式）}:$

$f'(x) = \displaystyle\lim_{\Delta x \to 0} \frac{f(x + \Delta x) – f(x)}{\Delta x}$

4.2. 導関数と記号

導関数とは、元の関数 $f(x)$ のすべての点における接線の傾きを返す関数です。

主に以下の記号で表記されます。

プライム記号: $f'(x)$ （エフプライムエックス）
- 定義式そのものの左辺として使用されます。
ライプニッツ記号: $\displaystyle\frac{dy}{dx}$ （ディーワイディーエックス）
- 平均変化率 $\mathbf{\Delta y / \Delta x}$ の極限操作という微分の成り立ちをそのまま反映したひとつの記号で、分数ではありません。
- $\Delta$（デルタ）が $\mathbf{d}$（ディー）に置き換わることで、「微小な変化」を意味します。したがって、$\displaystyle\frac{dy}{dx} = \displaystyle\lim_{\Delta x \to 0} \displaystyle\frac{\Delta y}{\Delta x}$ の関係が成り立ちます。

5. 定義式から導関数を導く：実践計算

微分における重要な目標のひとつは、計算ルール（公式）を覚えることではなく、その計算が成り立つ仕組み（原理）を理解することにあります。

ここでは、シンプルな非線形関数である $f(x) = x^2$ を定義式で解き、その導関数が $2x$ になることを証明してみましょう。

5.1. 使用する関数と定義式

関数（入力）: $f(x) = x^2$
定義式: $f'(x) = \displaystyle\lim_{\Delta x \to 0} \frac{f(x + \Delta x) – f(x)}{\Delta x}$

5.2. ステップ 1: 分子 $f(x + \Delta x) – f(x)$ の計算

まず、平均変化率の分子にあたる $y$ の変化量 $\Delta y$ を計算します。

① $f(x) = x^2$ に $x + \Delta x$ を代入し、展開します。
※ 「展開」に自信がない方はこちらの記事を参照ください。

$f(x + \Delta x) = (x + \Delta x)^2$
$ = x^2 + 2x(\Delta x) + (\Delta x)^2$

② 元の関数 $f(x) = x^2$ を引き算します。

$\Delta y = f(x + \Delta x) – f(x)$
$ = [x^2 + 2x(\Delta x) + (\Delta x)^2] – x^2$

③ $x^2$ が相殺され、次のように変化量 $\Delta y$ が求められます。

$\Delta y = 2x(\Delta x) + (\Delta x)^2$

5.3. ステップ 2: $\Delta x$ で約分する

次に、平均変化率の式 $\displaystyle\frac{\Delta y}{\Delta x}$ に代入し、分母の $\Delta x$ で約分（割り算）します。

① 前項「5.2.」で求めた変化量 $\Delta y$ を分子に、 $\Delta x$ を分母に置くと、以下のようになります。

$\displaystyle\frac{\Delta y}{\Delta x} = \displaystyle\frac{2x(\Delta x) + (\Delta x)^2}{\Delta x}$

② 分子を $\Delta x$ で括ると約分できるため、分母の $\Delta x$ が消滅します。

$\displaystyle\frac{\Delta x (2x + \Delta x)}{\Delta x} = 2x + \Delta x$

ポイント: ここで $\Delta x$ の約分に成功したため、「$0$ で割れない」という最初の数学的問題が解消されました。

5.4. ステップ 3: 極限の操作 $\lim_{\Delta x \to 0}$ を適用

最後に、約分された式 $2x + \Delta x$ に対して、瞬間の変化率を導くための極限操作 $\lim_{\Delta x \to 0}$ を適用します。

$f'(x) = \displaystyle\lim_{\Delta x \to 0} (2x + \Delta x)$

極限操作 $\lim_{\Delta x \to 0}$ により、$\Delta x$ は $0$ に限りなく近づくため、この項は実質的に無視できるほど小さくなります。
分母を消し去った今のタイミングであれば、$\Delta x$ に $0$ を代入しても問題ないことを意味します。

$f'(x) = 2x + 0 = 2x$

したがって、$f(x) = x^2$ の導関数（瞬間の変化率）は… 👇

$f'(x) = 2x$

この結果は、「$f(x) = x^2$ のグラフ上のどの点 $x$ を取っても、その点の傾き（接線の傾き）は $2x$ というルールで計算できる」ことを証明しています。

6. 導関数を求めるための公式

前章で、大変面倒な微分の定義式の計算を通じて、$f(x) = x^2$ の導関数が $f'(x) = 2x$ になることを証明しました。

あの面倒な極限計算は、原理を理解するために必要な儀式でした。
関数の傾きを求めるために、定義式を使って5章の手順で毎回計算する必要はないのです。

微分には、計算を劇的にシンプルにする「公式」が存在します。

6.1. べき乗の微分公式（$x^n$ の公式）

$f(x) = x^2$ のような多項式関数は、次の「べき乗の微分公式」一つで計算できます。

$f(x) = x^n \quad \mathbf{\rightarrow} \quad f'(x) = n x^{n-1}$

この公式が示すルールは非常にシンプルです。

指数 ($n$) を前に ($x$の左に) 出す。
指数 ($n$) を 1 減らす。

計算の例をいくつか示します。

$f(x) = x^{\mathbf{2}}$
- $n=\mathbf{2}$ より $2 x^{2-1}$
- 導関数は $2x^1 = \mathbf{2x}$
$f(x) = x^{\mathbf{3}}$
- $n=\mathbf{3}$ より $3 x^{3-1}$
- 導関数は $\mathbf{3x^2}$
$f(x) = x^{\mathbf{10}}$
- $n=\mathbf{10}$ より $10 x^{10-1}$
- 導関数は $\mathbf{10x^9}$

6.2. その他の主要な微分公式

べき乗の公式に加え、特に科学計算、AI、ゲーム開発などで頻繁に使われる関数を扱うために、以下に挙げる3種のカテゴリの公式を理解することが重要です。

6.2.1. 三角関数の公式

周期的な現象（振動、波、円運動など）を扱う際に使用されます。

関数 $f(x)$	導関数 $f'(x)$
$\sin(x)$	$\cos(x)$
$\cos(x)$	$-\sin(x)$

$\tan(x)$ は、公式のリストに加えませんでした。
その理由は、暗記するには公式そのものが難解ですし、$\tan(x)$ が $\sin(x)$ と $\cos(x)$ の割り算（商）であり、すでに紹介した公式と、新たに学ぶ「商の法則」を組み合わせれば導出できるからです。

商の法則とは、複数の関数が割り算でつながっている場合に適用する公式です。

商の法則の公式：

$\displaystyle\frac{g(x)}{h(x)} \rightarrow \displaystyle\frac{g'(x)h(x) – g(x)h'(x)}{[h(x)]^2}$

【参考】$\tan(x)$ の導出（理論）

$\tan(x) = \displaystyle\frac{\sin(x)}{\cos(x)}$ と見なし、この商の法則を適用し、さらに三角関数の基本公式 $\sin^2(x) + \cos^2(x) = 1$ を利用することで導関数が得られます。

$g(x) = \sin(x) \rightarrow g'(x) = \cos(x)$
$h(x) = \cos(x) \rightarrow h'(x) = -\sin(x)$

$\frac{d}{dx} \tan(x) = \displaystyle\frac{\cos(x)\cos(x) – \sin(x)(-\sin(x))}{\cos^2(x)}$

$= \displaystyle\frac{\cos^2(x) + \sin^2(x)}{\cos^2(x)}$

ここで、三角関数の基本公式 $\cos^2(x) + \sin^2(x) = 1$ を使用すると、次の導関数が得られます。

$\frac{d}{dx} \tan(x) = \frac{1}{\cos^2(x)}$

$\displaystyle \frac{1}{\cos(x)}$ は $\sec(x)$ (セカント) であるため、$\sec^2(x)$ と表記されることも多いです。

「基本的な関数の微分（$\sin, \cos$）と組み合わせの法則があれば、他の複雑な関数の微分も可能になる」という微分の強力な側面を示す良い例となります。

とはいえ、見ての通り導出プロセスは複雑なので、「公式を覚えた方が良い」という考え方もアリだと思います。

6.2.2. 指数関数・対数関数の公式

データの増減（成長や減衰）、確率の計算、そしてAI（特に活性化関数）で重要な役割を果たします。

関数 $f(x)$	導関数 $f'(x)$
$e^x$	$e^x$
$\ln(x) (自然対数)$	$-\displaystyle \frac{1}{x}$

6.2.3. 関数の組み合わせに関する公式

単純な関数を組み合わせることで、より複雑な関数が作られます。

これらは難易度が高いため、次セクションで補足説明します。

公式の名称	関数 $f(x)$	導関数 $f'(x)$
和・差の法則	$g(x) \pm h(x)$	$g'(x) \pm h'(x)$
積の法則	$g(x) \cdot h(x)$	$g'(x)h(x) + g(x)h'(x)$
合成関数の微分 (連鎖律)	$f(g(x))$	$f'(g(x)) \cdot g'(x)$

6.3. 【補足】関数の組み合わせに関する公式を理解する

前セクション最後の項「6.2.3.」で挙げた公式は、パッと見ただけではなかなか内容が分かりづらいかと思いますので、もう少し詳しく説明を加えていきます。

6.3.1. 和・差の法則：分解して考える

$g(x) \pm h(x) \quad \rightarrow \quad g'(x) \pm h'(x)$

上記の式は、和・差の法則を表しています。
これは、複数の関数が足し算や引き算でつながっている場合（例：$f(x) = x^2 + 3x$）、それらを個別に微分し、その結果得られた導関数同士を足し引きしても良い、というルールに基づいて導関数を導くことができます。

和・差の法則が成り立つ理由

微分は「瞬間の変化率」を求める操作です。

関数 $f(x) = x^2 + 3x$ の変化は、$x^2$ の変化と $3x$ の変化が独立して積み重なったものと言えます。
お皿を洗うスピードと、床を磨くスピードは、互いに影響し合わないのと同じです。

具体例：

$f(x) = x^3 + 5x^2$ を微分すると、($x^3$ の微分) + ($5x^2$ の微分)で、 $f'(x) = 3x^2 + 10x$ となります。

6.3.2. 積の法則：片方を固定して変化を測る

$g(x) \cdot h(x) \quad \rightarrow \quad g'(x)h(x) + g(x)h'(x)$

上記の式は、積の法則を表しています。
複数の関数が掛け算（積）でつながっているとき、関数を一つずつ順番に微分し、その結果を足し合わせるルールに基づいて導関数を導くことができます。

積の法則が成り立つ理由

$f(x) = g(x) \cdot h(x)$ の変化は、Gが変化した分とHが変化した分の合計だからです。
例えるなら、長方形の面積 $A = L \cdot W$ の変化です。

具体例：

$f(x) = \mathbf{x} \cdot \mathbf{\sin(x)}$ の微分は、次の二つの項の和で計算されます。

左側 ($x$) を微分し、右側 ($\sin(x)$) はそのまま掛けたもの: $(\mathbf{x})’ \cdot \sin(x) = \mathbf{1} \cdot \sin(x)$
左側 ($x$) をそのままにし、右側 ($\sin(x)$) を微分したもの: $x \cdot (\mathbf{\sin(x)})’ = x \cdot \mathbf{\cos(x)}$

したがって、これらの二つを足し合わせると、次の導関数が得られます。

$f'(x) = \mathbf{1} \cdot \sin(x) + x \cdot \cos(x)$

6.3.3. 合成関数の微分（連鎖律）：連動する変化を計算する

$f(g(x)) \quad \rightarrow \quad f'(g(x)) \cdot g'(x)$

上記の式は、関数の入れ子状態を表しています。
関数の中に別の関数が組み込まれている（入れ子になっている）とき、外側と内側を順番に微分して掛け合わせるルールに基づいて導関数を導くことができます。

※ AIのバックプロパゲーション（誤差逆伝播法）は、この連鎖律を何十層ものニューラルネットワークに対して逆方向に適用しているだけです。

合成関数の微分（連鎖律）が成り立つ理由

外側の変化は内側の変化に連動しているため、その連動の影響（連鎖）を掛け算で計算する必要があるからです。

$x$ が少し変化すると、まず内側 $g(x)$ が動き、その $g(x)$ の変化が外側 $f$ に伝わって最終的な変化 $f(g(x))$ が決まります。

具体例：$f(x) = \sin(x^2)$ の導出

$f(x) = \sin(x^2)$ の微分は、次の二つの項の積で計算されます。

外側の関数 ($\sin(\cdots)$) を微分（中身 $x^2$ はそのまま）：
- $\left(\mathbf{\sin}(\mathbf{x^2})\right)’ \rightarrow \mathbf{\cos(x^2)}$
内側の関数 ($x^2$) を微分したもの：
- $\left(\mathbf{x^2}\right)’ \rightarrow \mathbf{2x}$
- 中身の $x^2$ をべき乗の公式で微分しています。

したがって、これら二つの結果を掛け合わせると、次の導関数が得られます。

$f'(x) = \cos(x^2) \cdot 2x$

7. 微分がプログラミングで役立つ3つの具体例

微分（導関数）は、単なる数学の計算ではなく、「最適解」を見つけるための強力なツールです。
特に、AI、ゲーム、データ分析といった分野で不可欠な役割を果たします。

7.1. 🎮 ゲーム開発：リアルな「瞬間の速度と力」を計算する

ゲームエンジンは、キャラクターや物体が現実のように動くために、物理法則をシミュレーションします。

位置の関数: $y = f(t)$ (位置は時間 $t$ の関数)
微分の役割:
- 位置を時間 $t$ で微分すると、その瞬間の速度（$f'(t)$）が求められます。
- 速度をもう一度時間 $t$ で微分すると、その瞬間の加速度（力）が求められます。
実用例: 衝突後の正確な跳ね返り、重力の影響下での放物線の軌道、滑らかなアニメーションの動きなど、「次の瞬間、物体はどこへ、どれだけの力で動くか」を予測・計算するために微分がコード化されています。

7.2. 🤖 AI・機械学習：最も効率の良い「学習方向」を見つける

ディープラーニングモデルは、損失関数（Loss Function）と呼ばれる、パラメーター（重み）に対する誤差を示す巨大で複雑な関数を扱います。

課題: ある損失関数が最も小さくなる点（最も誤差が少ない、つまり最も賢い状態）を見つけたい。
微分の役割: 微分（導関数）を計算することで、現在の地点から損失が最も急激に減少する方向（勾配）を正確に知ることができます。

勾配の逆方向にパラメーターを少しずつ修正していくアルゴリズムが、勾配降下法 (Gradient Descent) です。

プログラマーは、この微分の原理を理解していなければ、AIがなぜ学習できるのか、また学習率（一歩の大きさ）をどう調整すべきかを本質的に理解することが極めて困難になります。

7.3. 📊 データ分析・最適化：最大利益を導く「限界値」

ビジネスや経済の分野では、利益やコストを関数としてモデル化し、その最適点を微分によって求めます。

課題: 生産量 $x$ に対する利益 $P(x)$ を最大にしたい。
微分の役割: 利益関数 $P(x)$ を微分して $P'(x)$（限界利益）を求めます。
- $P'(x) = 0$ となる点が、利益が最大または最小になる最適な生産量 $x$ です。
実用例: 「商品を一つ追加で生産したとき、利益がどう変化するか」という瞬間の効率（変化率）を計算し、最大利益を生む最適なポイントを導出するシステムに微分が組み込まれています。

7.4. ⚛️ 量子プログラミング：量子アルゴリズムのパラメータ最適化

当ブログで力を入れている量子プログラミングの分野でも、微分は量子アルゴリズムの効率を高めるために重要な役割を果たします。

アルゴリズム: 変分量子固有値ソルバー（VQE: Variational Quantum Eigensolver）など、量子コンピューターと古典コンピューターを組み合わせたハイブリッドアルゴリズムで利用されます。
微分の役割: 量子回路に含まれる回転ゲートのパラメータを、量子コンピューターの測定結果（期待値）に基づき、最も早く最適値へ収束するように更新するために、微分（勾配）情報が必要とされます。
実用例: 化学シミュレーションにおける分子のエネルギー最適化など、量子コンピューターの「答えの精度」を最大化するための学習プロセスにおいて、微分の概念が中核的な役割を果たします。

🔚 まとめ

本記事を通じて、微分の概念を「計算テクニック」としてではなく、「変化の本質」を捉えるための数学的なツールとして解説してきました。

微分の学習パスを振り返る

微分の概念を以下のステップで段階的に掘り下げてきました。

問題意識: 平均変化率（割線）では、正確な瞬間の傾きを捉えられない。
核心の解決: $\mathbf{\Delta x}$（変化量）を $\mathbf{0}$ に限りなく近づける極限 ($\lim$)の操作により、「$0$ 除算」問題を回避した。
導関数: 極限操作の結果として、瞬間の傾き（接線の傾き）を返す導関数 $\mathbf{f'(x)}$ が定義された。
実用化: 面倒な定義式の計算は原理理解のためであり、実務ではべき乗、連鎖律などのシンプルな公式を使う。

微分とは、「ある関数 $f(x)$ から、その瞬間の変化のルール（導関数 $f'(x)$）を導き出す操作」に他なりません。

プログラミング世界における微分の価値

ここで学んだ微分の知識は、単なる数学の試験対策ではありません。
これはもはや、現代のテクノロジーにおいて「最適化」と「シミュレーション」を実現するための必須スキルと言って過言ではないでしょう。

応用分野	微分の役割
ゲーム開発	物理法則に基づき、物体の瞬間の速度や加速度を計算し、リアルな動きを再現する。
AI・機械学習	損失関数（誤差）の曲面を効率よく降りるための、最も急な下降方向（勾配）を特定する。
量子コンピューティング	量子アルゴリズムのパラメータを、最も早く最適解に導くための更新方向を決定する。

次のステップへ

本記事を終えた読者の皆さまは、もはや微分の世界で迷子になることはありません。
微分の原理を知っていれば、複雑なAIのアルゴリズムを「勾配というルールで動く単純なもの」として理解できるようにもなります。

この微分の知識は、微積分学（Calculus）の後半のテーマである積分（Integration）へと繋がります。

微分：変化率（傾き）を求め、一点における瞬間を捉える。
積分：微小な変化（面積）をすべて積み重ねて、元の関数の全体（面積、総量）を求める。

微分と積分は、互いに逆の操作であり、微積分学の基本定理によって深く結びついています。
次の学習として「積分」の概念を学ぶことで、微積分学の全体像が完成するでしょう。

関数 \(f(x)\)	導関数 \(f'(x)\)
\(\sin(x)\)	\(\cos(x)\)
\(\cos(x)\)	\(-\sin(x)\)

関数 \(f(x)\)	導関数 \(f'(x)\)
\(e^x\)	\(e^x\)
\(\ln(x) (自然対数)\)	\(-\displaystyle \frac{1}{x}\)

公式の名称	関数 \(f(x)\)	導関数 \(f'(x)\)
和・差の法則	\(g(x) \pm h(x)\)	\(g'(x) \pm h'(x)\)
積の法則	\(g(x) \cdot h(x)\)	\(g'(x)h(x) + g(x)h'(x)\)
合成関数の微分 (連鎖律)	\(f(g(x))\)	\(f'(g(x)) \cdot g'(x)\)