前回の記事では、集合論の土台となる二つの基本的な記号、要素の所属 (\(\in\)) と集合の包含 (\(\subseteq\)) を理解し、集合の「箱」と「中身」の関係を明確にしました。
しかし、数学的構造を築くためには、単に存在する集合を識別するだけでなく、「二つの集合をどのように組み合わせるか」「集合から特定の要素を取り除くにはどうするか」といった操作(演算)の定義が必要です。
本記事では、集合論の最も重要な基本演算である、和集合 (Union)、共通部分 (Intersection)、そして補集合 (Complement) を学びます。
これらの演算がどのように集合を組み立て、また分解するのかを、定義とベン図を通して深く理解しましょう。
目次
1. 和集合(Union)の定義
和集合は、二つ以上の集合を「一つにまとめる」操作であり、集合論の演算の中でも直感的に理解しやすいものです。
1.1. 和集合の定義と記号
二つの集合 \(A\) と \(B\) の和集合とは、\(A\) に含まれる要素、または \(B\) に含まれる要素、あるいはその両方に含まれる要素のすべてを集めた新しい集合のことです。
- 記号: 和集合は、大文字アルファベットの「U」に似た記号 \(\mathbf{\cup}\) を使って表されます。
\(A \cup B\)
- 論理的な定義: 和集合 \(A \cup B\) は、論理的には「OR (または)」の条件で定義されます。形式的な定義式では、論理積の記号 \(\mathbf{\vee}\) や英語の \(\mathbf{\text{or}}\) が使用されます。
\(A \cup B = \{ x \mid x \in A \mathbf{\vee} x \in B \}\)
次のように「or」を使用して記述される場合もあります。
\(A \cup B = \{ x \mid x \in A \text{ or } x \in B \}\)
意味: \(A \cup B\) は、要素 \(x\) のうち、\(x\) が \(A\) に所属するか、あるいは \(x\) が \(B\) に所属するすべての \(x\) の集合である。
1.2. 和集合のベン図
和集合は、ベン図で視覚化すると、その意味が明確になります。
和集合 \(A \cup B\) は、\(A\) と \(B\) の領域を合わせたすべてを塗りつぶした領域に相当します。
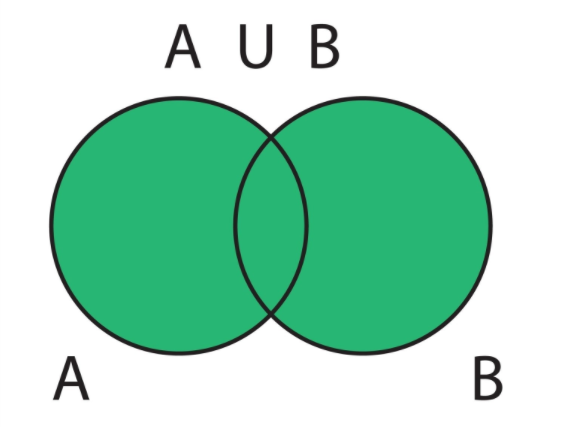
【例】次の集合 A, B の和集合を求めます。
- 集合 \(A = \{1, 2, 3\}\)
- 集合 \(B = \{3, 4, 5\}\)
このとき、和集合 \(A \cup B\) は、重複する要素 (3) を一つだけとみなし、すべてを合わせます。
\(A \cup B = \{1, 2, 3, 4, 5\}\)
2. 共通部分(Intersection)の定義
共通部分の演算は、和集合とは対照的に、複数の集合の間で「重なっている部分のみ」を抽出する操作です。
2.1. 共通部分の定義と記号
二つの集合 \(A\) と \(B\) の共通部分とは、\(A\) にも含まれ、かつ \(B\) にも含まれる要素のすべてを集めた新しい集合のことです。
- 記号: 共通部分は、和集合の記号 \(\cup\) を逆さにした記号 \(\mathbf{\cap}\)(キャップ)を使って表されます。
\(A \cap B\)
- 論理的な定義: 共通部分 \(A \cap B\) は、論理的には「AND (かつ)」の条件で定義されます。形式的な定義式では、論理積の記号 \(\mathbf{\wedge}\) や英語の \(\mathbf{\text{and}}\) が使用されます。
\(A \cap B = \{ x \mid x \in A \mathbf{\wedge} x \in B \}\)
次のように「or」を使用して記述される場合もあります。
\(A \cap B = \{ x \mid x \in A \text{ and } x \in B \}\)
2.2. 共通部分のベン図
共通部分は、ベン図で視覚化すると、その意味が非常に分かりやすいです。
共通部分 \(A \cap B\) は、\(A\) と \(B\) の領域が重なっている部分のみを塗りつぶした領域に相当します。
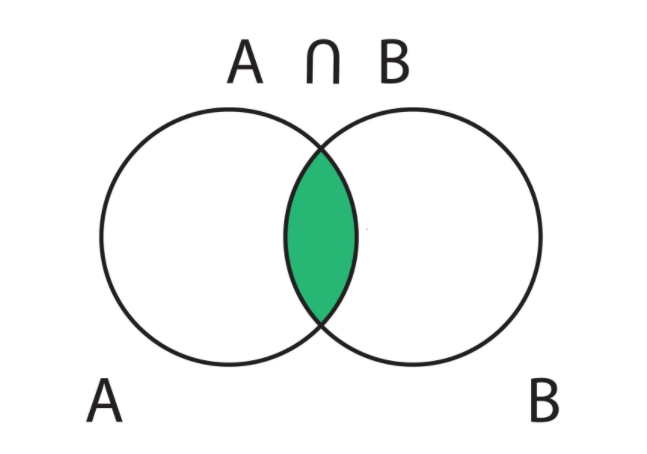
【例】次の集合 A, B の共通部分を求めます。
- 集合 \(A = \{1, 2, 3, 4\}\)
- 集合 \(B = \{3, 4, 5, 6\}\)
このとき、共通部分 \(A \cap B\) は、両方の集合に存在する要素のみを集めます。
\(A \cap B = \{3, 4\}\)
3. 補集合(Complement)の定義
補集合の演算は、これまで扱った和集合や共通部分と異なり、全体集合 \(U\) の存在が前提となります。
補集合は「特定の集合の外側にある部分」を切り出す操作です。
3.1. 補集合の定義と記号
集合 \(A\) の補集合とは、議論の対象となるすべての要素を含む全体集合 \(U\) の中で、\(A\) には含まれない要素のすべてを集めた新しい集合のことです。
- 記号: 補集合は、集合 \(A\) の右上に「c」または、真上に「バー」を付けて表されます。また、Aの右上にプライムを付ける記述もあります。それぞれ、「エー・コンプリメント (A complement)」、「エー・バー (A bar)」、「エー・プライム (A prime)」と読みます。
\(\mathbf{A^c}\)
または
\(\mathbf{\bar{A}}\)
または
\(\mathbf{A’}\)
- 論理的な定義: 補集合 \(A^c\) は、論理的には「NOT (ではない)」の条件で定義されます。一般的な定義式では、所属の否定を意味する記号 \(\mathbf{\notin}\) を用います。
\(A^c = \{ x \in U \mid x \notin A \}\)
意味: \(A^c\) は、\(U\) の要素 \(x\) のうち、\(x\) が \(A\) に属さないすべての \(x\) の集合である。
3.2. 補集合のベン図
補集合を理解するには、全体集合 $U$ が不可欠です。
補集合 \(A^c\) は、全体集合 \(U\) の長方形の領域のうち、集合 \(A\) の円の外側を塗りつぶした領域に相当します。
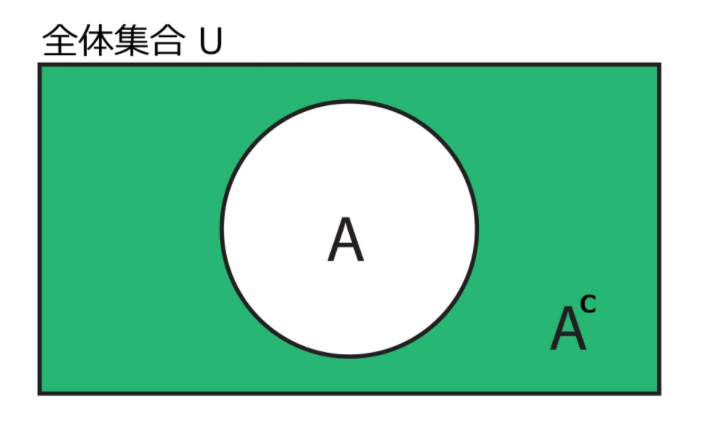
【例】次の集合 A, B の補集合を求めます。
- 全体集合 \(U = \{1, 2, 3, 4, 5\}\)
- 集合 \(A = \{1, 2, 3\}\)
このとき、補集合 \(A^c\) は \(U\) の要素のうち \(A\) に含まれないものです。
\(A^c = \{4, 5\}\)
4. 基本演算の代数的性質
和集合 (\(\cup\))、共通部分 (\(\cap\))、補集合 (\(^c\)) は、単に集合を組み合わせるだけでなく、代数的な法則に従って構造化されています。
これらの法則は、集合に関する複雑な命題を簡略化したり、証明したりする際に不可欠です。
4.1. 交換法則と結合法則
以下の法則は、数の加法や乗法と同じように、演算を行う順序に関する基本的なルールです。
- 交換法則: 集合の順序を入れ替えても結果は同じ
- 結合法則: 3つ以上の集合を扱うとき、計算の順序を変えても結果は同じ
| 法則名 | 和集合 (\(\cup\)) | 共通部分 (\(\cap\)) |
|---|---|---|
| 交換法則 | \(A \cup B = B \cup A\) | \(A \cap B = B \cap A\) |
| 結合法則 | \((A \cup B) \cup C = A \cup (B \cup C)\) | \((A \cap B) \cap C = A \cap (B \cap C)\) |
4.2. 分配法則
分配法則は、二つの異なる演算(\(\cup\) と \(\cap\))が混在する場合に、集合をどのように展開できるかを示します。
数学の \((\text{数}) \times (\text{和})\) の分配法則 \(a \times (b + c) = (a \times b) + (a \times c)\) に似ていますが、集合論では二つの演算が相互に分配可能なのが特徴です。
- 共通部分の和集合に対する分配法則
\(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)
- 和集合の共通部分に対する分配法則
\(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)
4.3. ド・モルガンの法則 (De Morgan’s Laws)
すべての法則の中で、最も強力で頻繁に使用されるのがド・モルガンの法則です。
これは、補集合と和集合/共通部分の関係を示します。
ド・モルガンの法則は、「括弧の外側の補集合は、括弧を外して各項に補集合の記号を付加し、中の演算子を反転させる」と覚えます。
- 和集合の補集合:補集合をかけると、和集合 (\(\cup\)) が共通部分 (\(\cap\)) に反転する。
\((A \cup B)^c = A^c \cap B^c\)
- 共通部分の補集合:補集合をかけると、共通部分 (\(\cap\)) が和集合 (\(\cup\)) に反転する。
\((A \cap B)^c = A^c \cup B^c\)
本章で紹介した各法則は、論理学や確率論でも重要な役割を果たします。
特にド・モルガンの法則は、後の複雑な集合の証明を行う上での強力な武器となります。
まとめ
本記事では、集合論の土台の上に、数学的な構造を構築するための三つの基本的な演算、すなわち和集合、共通部分、補集合を学びました。
三大基本演算の役割は、次の通りです。
- 和集合: \(\mathbf{\cup}\)
- or (または) の意味を持ち、二つの集合の要素をすべて「集める」操作
- 共通部分: \(\mathbf{\cap}\)
- and (かつ) の意味を持ち、二つの集合の「重なり」のみを「抽出する」操作
- 補集合: \(\mathbf{A^c}\)
- not (ではない) の意味を持ち、全体集合 \(U\) の中で \(A\) に含まれない要素を「切り出す」操作
そして、これらの演算を組み合わせた際に現れる、最も重要な法則がド・モルガンの法則です。
この法則は、「括弧の外側の補集合は、括弧を外して各項に補集合の記号を付加し、中の演算子を反転させる」という変換ルールを提供します。
\((A \cup B)^c = A^c \cap B^c\)
\((A \cap B)^c = A^c \cup B^c\)
ここまでで、集合の基本、関係、そして演算という道具が揃いました。
次回からは、【集合論応用】シリーズとして衣替えし、入門シリーズで得た知識を「現実の関係性」に応用し、数学的な構造へと昇華させましょう。
テーマは、直積集合(デカルト積)と写像(集合論における関数の概念)を扱う予定です。
- 直積集合: 集合を掛け合わせることで、どのように座標や順序といった「関係」が生まれるのか。
- 写像: 数学における「関係」の中から、特定のルールに従った「関数」をどのように定義するのか。



コメント